5.5逆波兰表达式求值（LC150-M）

news2024/11/25 6:37:29

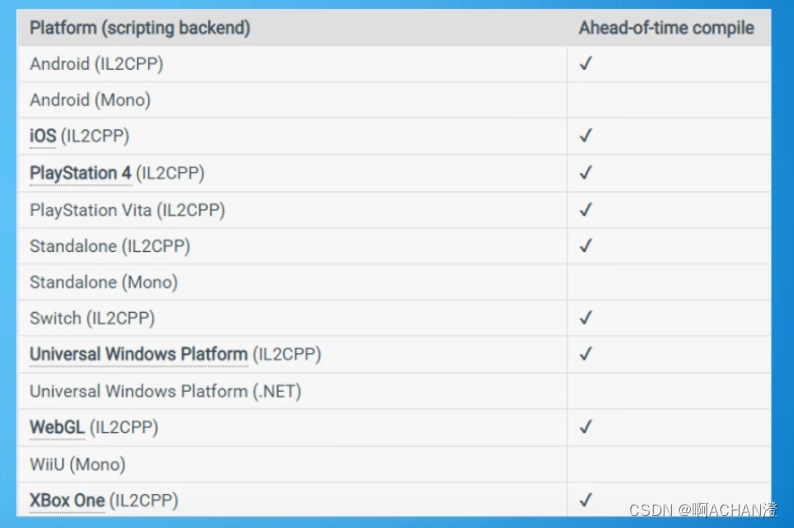
算法：

其实就是后缀表达式。

本题中每一个子表达式要得出一个结果，然后拿这个结果再进行运算，那么这岂不就是一个相邻字符串消除的过程，和1047.删除字符串中的所有相邻重复项 (opens new window)中的对对碰游戏是不是就非常像了。

看到数字就push入栈

看到操作符，就对栈顶的2个元素运算

然后把结果继续push入栈

可以用到的函数：

eval() 是一个内置函数，用于将字符串作为表达式进行求值并返回结果。

它的语法如下： eval(expression, globals=None, locals=None)

`expression` 是一个字符串，表示要求值的表达式。

`globals` (可选) 是一个字典，用于指定全局命名空间中的变量和函数。如果未提供该参数，则使用当前全局命名空间。

`locals` (可选) 是一个字典，用于指定局部命名空间中的变量和函数。如果未提供该参数，则使用当前局部命名空间。

`eval()` 函数的工作原理如下：

1. 接收一个字符串表达式作为输入。

2. 解析并评估表达式中的代码。

3. 返回表达式的结果。返回值是一个float

`eval()` 函数可以用于执行简单的数学运算、执行动态代码和计算复杂的表达式。它非常灵活，可以接受包含变量、函数调用和各种操作符的表达式。然而，需要注意的是，使用 `eval()` 函数时存在一些安全风险。因为它可以执行任意的代码，所以如果表达式来自不受信任的来源，可能会导致安全漏洞。因此，在实际应用中，应该谨慎使用 `eval()` 函数，并确保只对可信的输入进行求值。如果您有任何进一步的问题，请随时提问。

调试过程：

class Solution:
    def evalRPN(self, tokens: List[str]) -> int:
        self.stack = []
        ##举例12/
        for item in tokens:
            if item != "+" and item != "-" and item != "*" and item != "/":
                self.stack.append(item)
                #压入1、2
            else:
                
                second_num = self.stack.pop()#先弹出的是2
                first_num = self.stack.pop()#再弹出的是1
                #eval计算的结果为float：0.50000，所以要转成int，变成0
                res = int(eval(f"{first_num}{item}{second_num}"))
                #再把计算的结果push入栈，继续计算
                self.stack.append(res)
        
        return int(res)## 如果一开始只有一个数，那么会是字符串形式的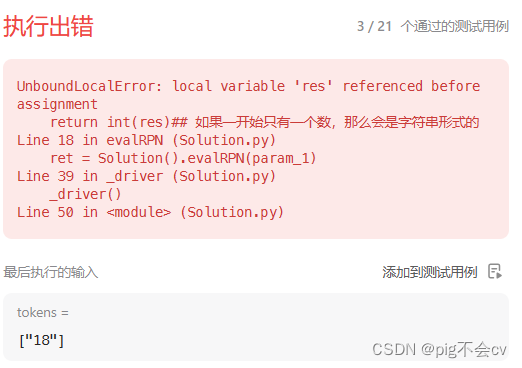

原因：在 `res` 变量被引用之前，它没有被赋值。在您的代码中，`res` 变量只在 `else` 语句块中定义和使用。如果 `tokens` 列表为空，或者不包含任何运算符，那么 `else` 语句块将不会执行，导致 `res` 变量没有被赋值。

正确代码：

class Solution:
    def evalRPN(self, tokens: List[str]) -> int:
        self.stack = []
        ##举例12/
        for item in tokens:
            if item != "+" and item != "-" and item != "*" and item != "/":
                self.stack.append(item)
                #压入1、2
            else:
                
                second_num = self.stack.pop()#先弹出的是2
                first_num = self.stack.pop()#再弹出的是1
                #eval计算的结果为float：0.50000，所以要转成int，变成0
                res = int(eval(f"{first_num}{item}{second_num}"))
                #再把计算的结果push入栈，继续计算
                self.stack.append(res)
        
        return int(self.stack.pop())# 如果一开始只有一个数，那么会是字符串形式的

注意：

eval那里有个"f"

在Python中，`f` 是格式化字符串（Formatted String）的前缀，用于创建包含表达式的字符串。

通过在字符串前面加上 `f` 前缀，可以在字符串中插入变量、表达式或函数调用的结果。

如果没有f，那么字符串将不再是一个格式化字符串，而是一个普通的字符串。

在这种情况下，`eval()` 函数将直接对字符串 `'{first_num} {item} {second_num}'` 进行求值，而不会替换其中的变量。

时间空间复杂度

时间复杂度分析：

遍历 `tokens` 列表，时间复杂度为 O(n)，其中 n 是 `tokens` 列表的长度。
在遍历过程中，对于每个操作符，执行了一次 `self.stack.pop()` 操作，时间复杂度为 O(1)。
使用 `eval` 函数进行表达式计算，时间复杂度取决于表达式的长度和复杂度。在最坏情况下，表达式长度为 O(n)，其中 n 是操作数和操作符的总数。
将计算结果压入栈中，时间复杂度为 O(1)。

综上所述，总体时间复杂度为 O(n)。