精读《算法题 - 二叉树中的最大路径和》

news2024/11/25 14:48:03

今天我们看一道 leetcode hard 难度题目：二叉树中的最大路径和。

题目

二叉树中的路径被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中至多出现一次。该路径至少包含一个节点，且不一定经过根节点。

路径和是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其最大路径和。

示例1：

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

思考

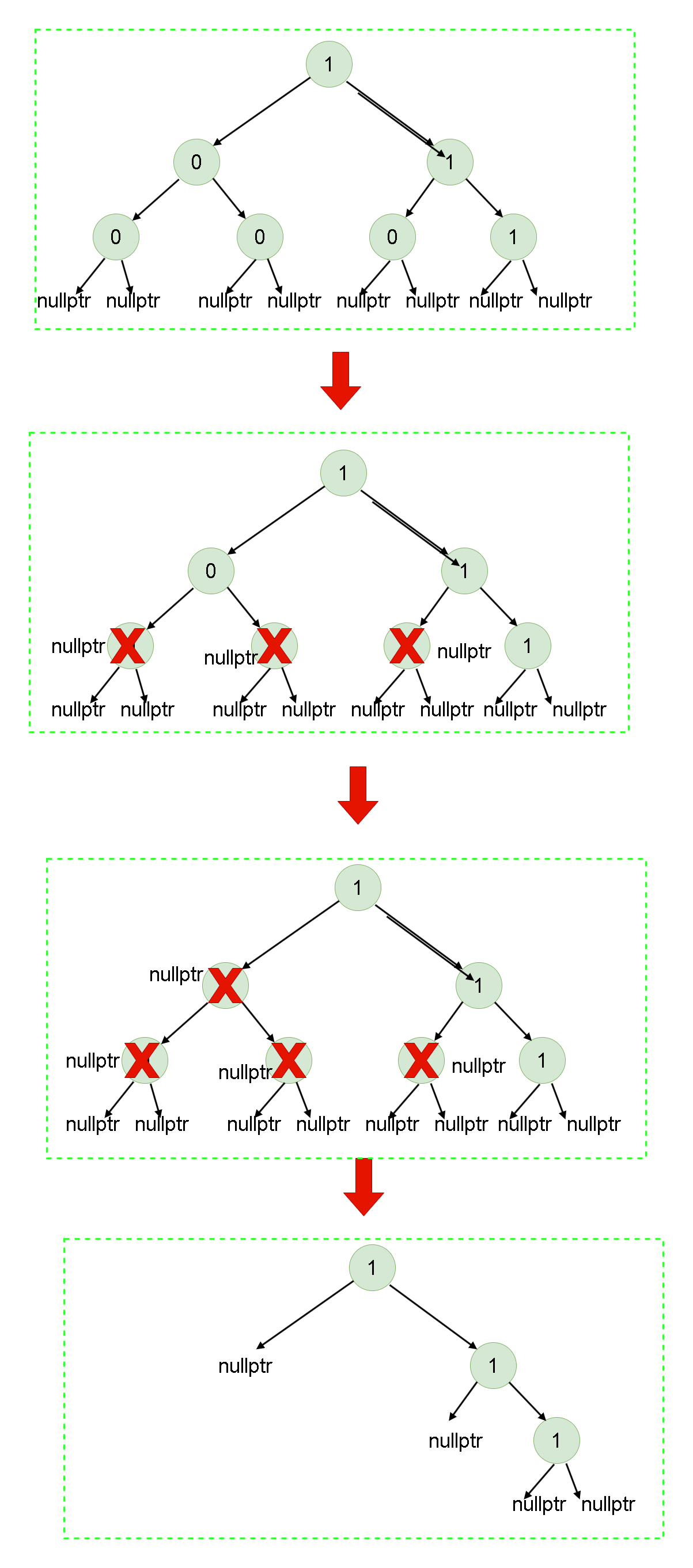
第一想法是，这道题不安常理出牌，因为路径竟然不是自上而下的，而是可以横向蛇形游走的，如下图：

尝试动态规划

第二想法是，这种蛇形游走的路径，求路径最大值应该用什么方法？大概率是暴力解法，因为 必须遍历完所有节点，才知道是否有更大的值的可能性，而应对暴力解法最好的策略是动态规划，那么应该如何定义状态？经过一番思考，二叉树点到点之间仅有唯一一条路径，如果我们能枚举计算经过每个点的所有可能路径的最大值，那么找到其中最大的就可以得到答案。但可惜的是，以 “点” 为变量没办法写转移方程。

以暴力解法为基础思考

此时要切换想法，经过一些思考，我决定以正序角度模拟一下寻找最大路径和的思路：首先选择一个起点，找到以该起点开始的最大路径合。那么从该起点就有最多 3 种走法，分别是向根节点走、左子节点、右子节点走：

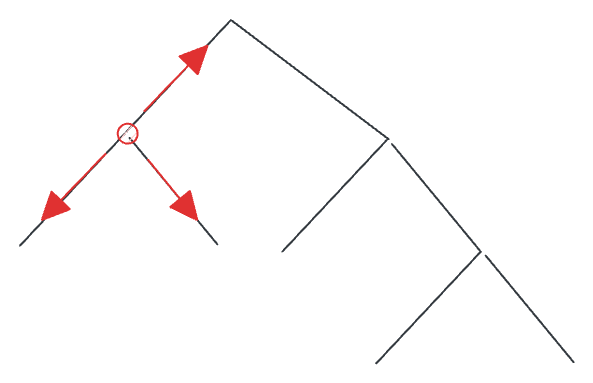
最暴力的解法是遍历每个点，把所有方向都走一遍，找到所有可能的最大值。 这无疑是一个最有效的兜底解法，但效率太低，那么为了提升效率，假设一条路径的最大潜力已经计算过一次了，那么一条新路径经过时，就没必要重新算一遍。所以我们要寻找每个方向的最大贡献。

寻找每个方向的最大贡献

假设我们提前找到了经过每个点的最大贡献如下：

根节点的最大贡献 10 的含义为：从 3 向根节点走，所有可能路径能带来的最大正数收益为 10。所以此时最大路径和显然为：5 + 3 + 10 = 18.

但此时矛盾来了，根节点的最大贡献 10 是从 3 向根节点走的角度定义的，它有两个致命问题：

每个节点的最大贡献最好只能有一个数字，依赖方向的话复杂度太高了。
如果要依赖方向，那么从根节点右子节点走向根节点的最大贡献，其实依赖从左子结点出发的最大贡献，相互死锁了。

这种最大贡献几乎不可能找到，再花时间思考只是浪费时间，所以我们要改变策略了。再想想二叉树的特征是什么，怎么样能最稳定的定义每个节点的最大贡献？很容易想到的是以树的深度来定义，即 以当前节点向子节点遍历时，能带来的最大贡献。这种最大贡献是比较容易计算的。

每个子树的最大贡献

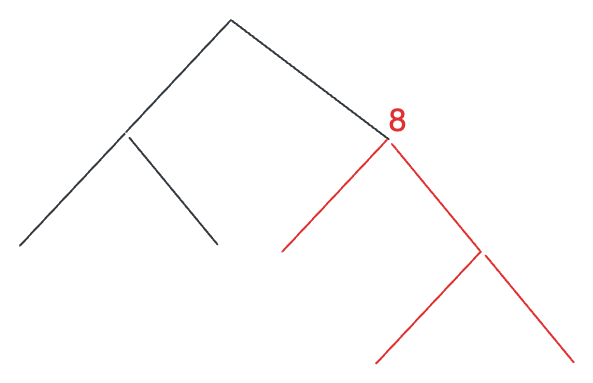
如上图所示，以 8 这个节点的子树，假设通过一系列递归找到，它能提供的最大贡献就是 8，且这个贡献必须是一条没有分叉的线，这样这个最大贡献对于它的父节点才有意义，即父节点可以把这个节点连上，形成一条更长的没有分叉的线。如果子线都有分叉，整条线就会存在分叉，就不符合题意了。

这个 8 很容易计算，从叶子结点向上推，找到最大且大于 0 的子节点连成线即可。

但回到这道题，如果我们仅仅计算了每个点所在子树的最大贡献，那么其最大值仅是垂直的线中的最大值，没有考虑到该题路径可以横向蛇形游走的特性：

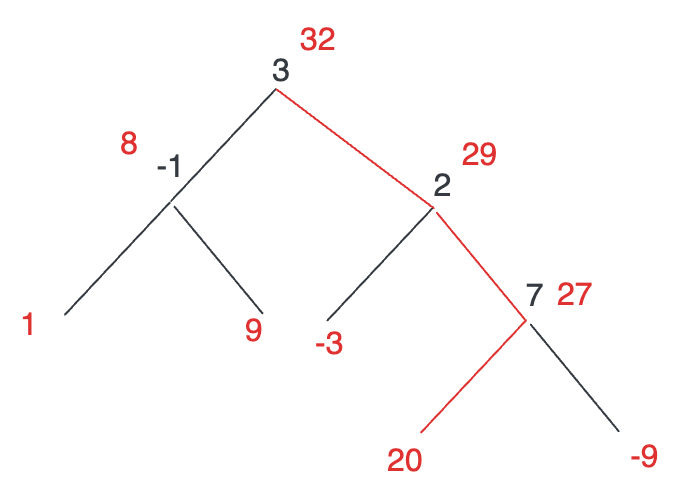
如上图所示，红色的数字为以该点开始的子树的最大贡献，那么根节点 32 其实就是红色路径提供的路径和，对于纵向走位来说是最大的，但并不是本题最大的。本题最大的值，还得把下图红色的路径考虑上，变成一个横向的线，此时最大值达到了 32 + 8 = 40：

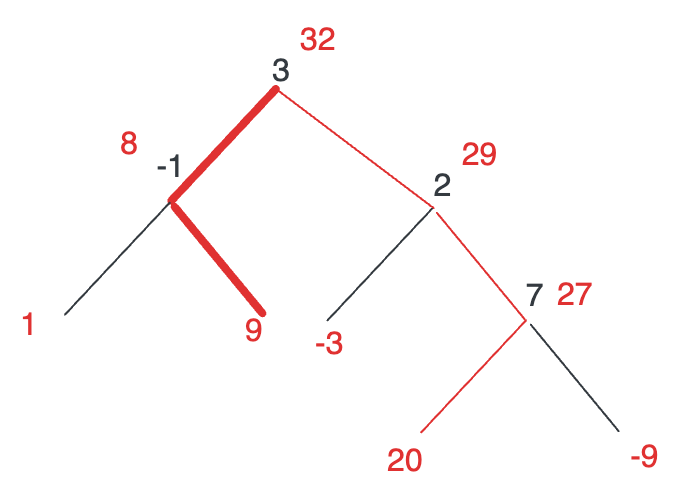
但其实要把线变成横向的，也仅需要多考虑另一个子节点而已，因为所有子树的最大贡献已经提前算好，根本无需再深入子子节点。也就是说，在计算最大路径和时（重要内容字体加粗！）：

经过该点的最大路径和，要同时考虑该点 + 左右子树最大贡献，也就是此时路径会形成类似倒扣的 U 型。
但该节点的最大贡献呢，只能考虑该点 + 左 or 右子树最大贡献的，不能形成倒扣的 U 型，因为这个最大贡献需要被其父节点作第 1 条规则时考虑，如果此时已经是倒扣 U 型了，那么父节点再分叉一次倒扣的 U 型，就不是一条线了，可能会形成如下图所示奇怪的形状:

这就是本题最精彩的思考点。

代码实现

想通了之后，代码就很简单了：

function maxPathSum(root: TreeNode | null): number {
  let maxValue = -Infinity

  function maxOneLinePathByNode(node: TreeNode): number {
    // 如果节点为空，返回负无穷，必然不会被最大路径和带上
    if (node === null) return -Infinity

    // 左子树最大贡献(如果为负数则为 0，表示不带上左子树)
    const leftChildMaxValue = Math.max(maxOneLinePathByNode(node.left), 0)
    // 右子树最大贡献 - 同理
    const rightChildMaxValue = Math.max(maxOneLinePathByNode(node.right), 0)

    // 经过该点的最大路径和
    const currentPointMaxValue = node.val + leftChildMaxValue + rightChildMaxValue
    // 刷新 maxValue
    maxValue = Math.max(maxValue, currentPointMaxValue)

    // 返回不分叉的子树最大贡献
    return node.val + Math.max(leftChildMaxValue, rightChildMaxValue)
  }

  maxOneLinePathByNode(root)

  return maxValue
};

因为从根节点开始递归，可以算出所有子树的最大贡献，把经过每一个点的路径都考虑到了，所以答案是不重不漏的。