1. 题目链接：814. 二叉树剪枝

2. 题目描述：

给你二叉树的根结点 root ，此外树的每个结点的值要么是 0 ，要么是 1 。

返回移除了所有不包含 1 的子树的原二叉树。

节点 node 的子树为 node 本身加上所有 node 的后代。

示例 1：

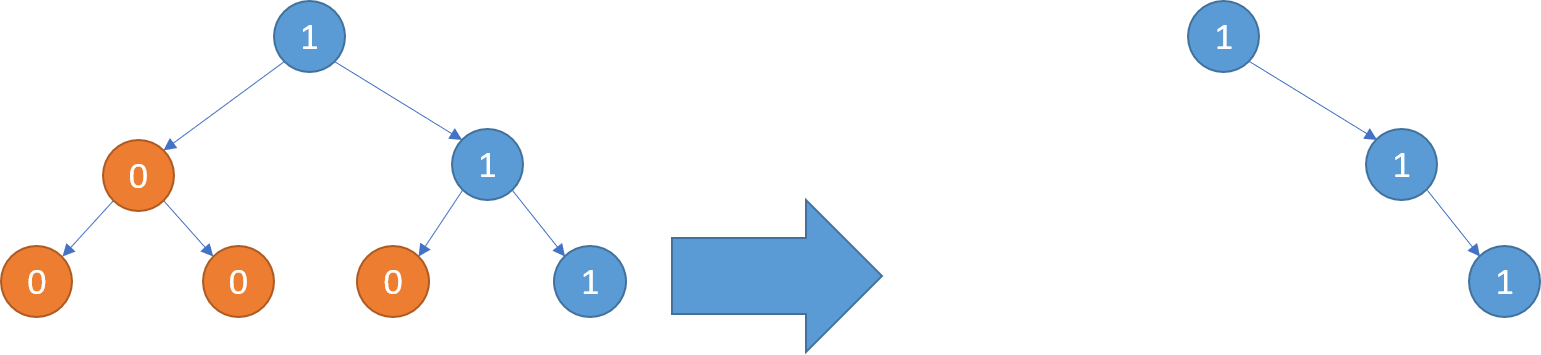
输入：root = [1,null,0,0,1]
输出：[1,null,0,null,1]
解释：
只有红色节点满足条件“所有不包含 1 的子树”。 右图为返回的答案。

示例 2：

输入：root = [1,0,1,0,0,0,1]
输出：[1,null,1,null,1]

示例 3：

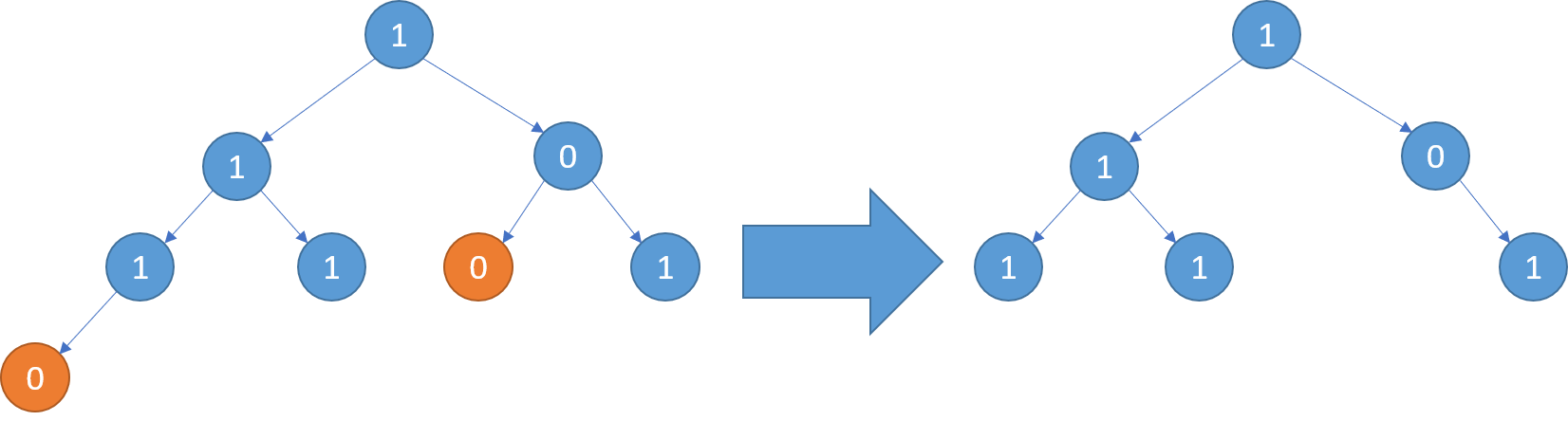
输入：root = [1,1,0,1,1,0,1,0]
输出：[1,1,0,1,1,null,1]
提示：

• 树中节点的数目在范围 [1, 200] 内
• Node.val 为 0 或 1

3. 解法（后续遍历）

后续遍历按照左子树->右子树->根节点的顺序遍历二叉树的所有节点，通常用于父节点的状态依赖于子节点状态的题目

3.1 算法思路：

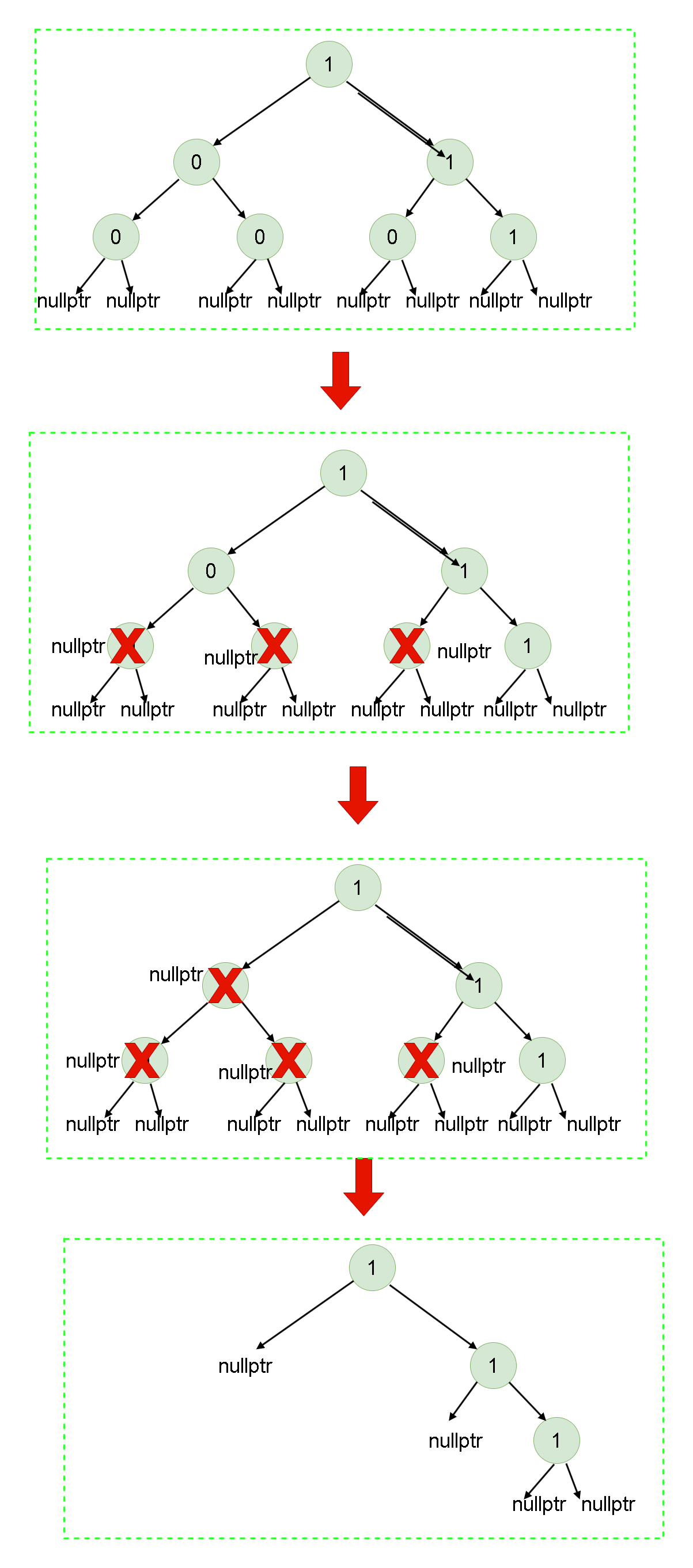
1. 在删除叶子节点时，其父节点很可能会成为新的叶子节点。因此，在处理完子节点后，我们仍然需要处理当前节点。
2. 通过使用后续遍历，我们可以逐步删除叶子节点，并且保证删除后的节点仍然满足删除操作的要求。这样，我们可以较为方便地实现删除操作，而不会影响最终的结果
3. 若处理结束后所有叶子节点的值均为1，则所有子树均包含1，此时可以返回

3.2 算法流程：

1. 递归出口：当传入节点为空时，不做任何处理
2. 递归处理左子树
3. 递归处理右子树
4. 处理当前节点：判断该节点是否为叶子节点（即左右子节点均被删除，当前节点成为叶子节点），并且节点的值为0
   1. 如果是，就删除掉
   2. 如果不是，就不做任何处理
      

3.3 C++算法代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* pruneTree(TreeNode* root) {
        if(root==nullptr) return nullptr;
        root->left=pruneTree(root->left);
        root->right=pruneTree(root->right);
        if(root->left==nullptr&&root->right==nullptr&&root->val==0)
        {
            delete root;
            root=nullptr;
        }
        return root;
    }
};