版本说明
当前版本号[20231106]。
| 版本 | 修改说明 |
|---|---|
| 20231106 | 初版 |
目录
文章目录
- 版本说明
- 目录
- 两数相加
- 题目
- 解题思路
- 代码思路
- 补充说明
- 参考代码
- 二叉树的锯齿形层序遍历
- 题目
- 解题思路
- 代码思路
- 参考代码
- 解数独
- 题目
- 解题思路
- 代码思路
- 补充说明
- 参考代码
两数相加
题目
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
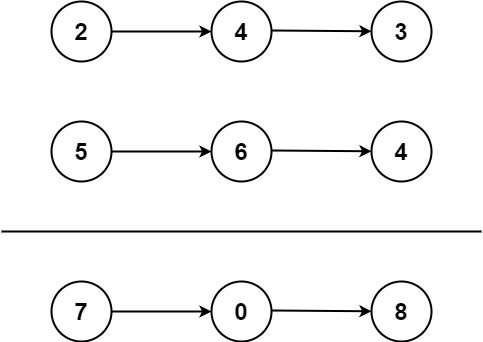
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
提示:
- 每个链表中的节点数在范围
[1, 100]内 0 <= Node.val <= 9- 题目数据保证列表表示的数字不含前导零
解题思路
- 创建一个新的空链表,用于存储相加后的结果。
- 遍历第一个链表,将每个节点的值累加到结果链表的对应位置上。
- 遍历第二个链表,将每个节点的值累加到结果链表的对应位置上。
- 如果结果链表的长度小于两个输入链表的长度之和,则在结果链表的末尾添加足够数量的0。
- 返回结果链表。
代码思路
-
创建一个临时变量
lrr,将其初始化为l1。ListNode lrr = l1; // 创建一个临时节点,用于存储结果链表的头节点 -
使用
while循环遍历链表l1和l2,直到两个链表都遍历完毕且当前节点的值小于10。 -
在每次循环中,将
l1和l2当前节点的值相加,并将结果存储在l1的当前节点中。while (true) { // 将当前节点的值加上下一个节点的值 l1.val = l1.val + l2.val; } -
如果
l1或l2的下一个节点为空,则创建一个新的节点并将其赋值给相应的下一个节点。// 如果当前节点是最后一个节点,则创建一个新的节点,并将其指针指向下一个节点 if (l1.next == null) { l1.next = new ListNode(0); } // 如果下一个节点是最后一个节点,则创建一个新的节点,并将其指针指向下一个节点 if (l2.next == null) { l2.next = new ListNode(0); } -
如果
l1的当前节点的值大于等于10,则需要进位。将l1的当前节点的值减去10,并将进位值加到下一个节点的值上。// 如果当前节点的值大于等于10,则将当前节点的值减去10,并将下一个节点的值加1 if (l1.val >= 10) { l1.val = l1.val - 10; l1.next.val += 1; } -
更新
l1和l2的指针,使其指向下一个节点。// 将当前节点和下一个节点分别向后移动一位 l1 = l1.next; l2 = l2.next; } -
当循环结束时,返回临时变量
lrr,即相加后的结果链表的头节点。
// 返回结果链表的头节点
return lrr;
补充说明
解决链表算法题目中,我们一般要建一个链表节点类ListNode用于构建链表数据结构。
下面定义的是一个链表节点类ListNode。这个类有三个构造函数:
- 默认构造函数,不传入参数时,节点值为0,指针为空。
- 传入一个整数作为节点值,指针为空。
- 传入一个整数和一个指向下一个节点的指针。
// 定义链表节点类
class ListNode {
int val; // 节点值
ListNode next; // 指向下一个节点的指针
ListNode() {
// 默认构造函数,不传入参数时,节点值为0,指针为空
}
ListNode(int val) {
// 传入一个整数作为节点值,指针为空
this.val = val;
}
ListNode(int val, ListNode next) {
// 传入一个整数和一个指向下一个节点的指针
this.val = val;
this.next = next;
}
}
扩展——这个类还可以用于实现以下功能:
- 创建链表:使用构造函数创建具有不同值和结构的节点,并将它们链接在一起形成链表。
- 遍历链表:通过访问节点的next属性,可以逐个访问链表中的每个节点,并对节点的值进行操作或处理。
- 插入节点:可以在链表的任意位置插入新的节点,通过更新相应节点的next指针来实现。
- 删除节点:可以根据给定的条件删除链表中的特定节点,通过更新相应节点的next指针来实现。
- 查找节点:可以根据给定的条件在链表中查找特定的节点,并通过遍历链表来找到目标节点。
- 修改节点:可以通过更新节点的值来修改链表中的特定节点。
- 统计链表长度:可以遍历链表并计数节点的数量,以获取链表的长度。
- 判断链表是否为空:可以检查链表的头节点是否为null来判断链表是否为空。
- 反转链表:可以将链表中的节点顺序颠倒过来,使头节点指向尾节点,尾节点指向头节点。
- 合并两个有序链表:可以将两个有序的链表合并成一个新的有序链表。
参考代码
以下代码用于实现两个链表表示的数字相加。
其中,ListNode类表示链表节点,包含一个整数值val和一个指向下一个节点的指针next。
Solution类中的addTwoNumbers方法接受两个链表l1和l2作为参数,返回它们的和所表示的链表。
class ListNode {
int val;
ListNode next;
ListNode() {
}
ListNode(int val) {
this.val = val;
}
ListNode(int val, ListNode next) {
this.val = val;
this.next = next;
}
}
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode lrr = l1;
while (true) {
l1.val = l1.val + l2.val;
if (l1.next == null && l2.next == null && l1.val < 10) {
break;
}
if (l1.next == null) {
l1.next = new ListNode(0);
}
if (l2.next == null) {
l2.next = new ListNode(0);
}
if (l1.val >= 10) {
l1.val = l1.val - 10;
l1.next.val += 1;
}
l1 = l1.next;
l2 = l2.next;
}
return lrr;
}
}
二叉树的锯齿形层序遍历
题目
给定一个二叉树,返回其节点值的锯齿形层序遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/
9 20
/
15 7

返回锯齿形层序遍历如下:
[
[3],
[20,9],
[15,7]
]

解题思路
- 实现二叉树的锯齿形层序遍历,即先按照从左到右的顺序遍历当前层的节点,然后再按照从右到左的顺序遍历下一层的节点,以此类推。
- 为了实现锯齿形层序遍历,我们可以使用两个栈来辅助遍历。一个栈用于存储每一层的节点,另一个栈用于控制遍历的方向。
- 初始时,将根节点压入第一个栈中,并将遍历方向设为从左到右(
postive为true)。 - 进入一个循环,条件为第一个栈不为空。在循环中,首先创建一个新的栈和一个新的链表,用于存储当前层的节点值和子节点。
- 进入另一个循环,条件为第一个栈不为空。在这个循环中,弹出第一个栈的顶部元素,将其值添加到当前层的链表中。然后根据遍历方向,将当前节点的左子节点和右子节点按照不同的顺序压入新的栈中。具体来说,如果**遍历方向为从左到右,则先压入左子节点,再压入右子节点;**否则,先压入右子节点,再压入左子节点。
- 在内部循环结束后,将新的栈赋值给第一个栈,并将当前层的链表添加到结果列表中。同时,将遍历方向取反。
- 当外部循环结束时,返回结果列表作为最终的输出。
代码思路
1、首先定义了一个名为TreeNode的类,表示二叉树的节点。
// 定义二叉树节点类
public class TreeNode {
int val; // 节点值
TreeNode left; // 左子节点
TreeNode right; // 右子节点
TreeNode(int x) { // 构造函数
val = x;
}
}
2、以及一个名为Solution的类,其中包含一个名为zigzagLevelOrder的方法。该方法接受一个TreeNode类型的参数root,表示二叉树的根节点,并返回一个List<List<Integer>>类型的结果,表示锯齿形层序遍历的结果。
// 定义解决方案类
class Solution {
// 实现锯齿形层序遍历方法
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> list = new LinkedList<>(); // 存储结果的列表
……
return list; // 返回结果列表
}
}
3、在zigzagLevelOrder方法中,首先创建一个空的LinkedList对象list,用于存储结果。然后判断根节点是否为空,如果为空则直接返回空列表。接下来,创建两个栈stack1和stack2,并将根节点压入stack1中。同时,定义一个布尔变量postive,初始值为true,用于指示当前层的遍历方向。
if (root == null) { // 如果根节点为空,直接返回空列表
return list;
}
Stack<TreeNode> stack1 = new Stack<>(); // 创建第一个栈,用于存储当前层的节点
stack1.push(root); // 将根节点压入栈中
boolean postive = true; // 初始化遍历方向为从左到右
4、接下来进入一个循环,条件为stack1不为空。在循环中,首先创建一个新的栈stack2和一个空的链表subList,用于存储当前层的节点值和子节点。然后进入另一个循环,条件为stack1不为空。在循环中,弹出stack1的顶部元素,将其值添加到subList中。根据postive的值,将当前节点的左子节点和右子节点按照不同的顺序压入stack2中。具体来说,如果postive为true,则先压入左子节点,再压入右子节点;否则,先压入右子节点,再压入左子节点。
while (!stack1.isEmpty()) { // 当栈不为空时,继续遍历
Stack<TreeNode> stack2 = new Stack<>(); // 创建第二个栈,用于存储下一层的节点
List<Integer> subList = new LinkedList<>(); // 创建子列表,用于存储当前层的节点值
while (!stack1.isEmpty()) { // 当栈不为空时,继续遍历
TreeNode current = stack1.pop(); // 弹出栈顶元素,即当前层的一个节点
subList.add(current.val); // 将当前节点的值添加到子列表中
if (postive) { // 如果遍历方向为从左到右
if (current.left != null) { // 如果当前节点有左子节点
stack2.push(current.left); // 将左子节点压入栈中
}
if (current.right != null) { // 如果当前节点有右子节点
stack2.push(current.right); // 将右子节点压入栈中
}
} else { // 如果遍历方向为从右到左
if (current.right != null) { // 如果当前节点有右子节点
stack2.push(current.right); // 将右子节点压入栈中
}
if (current.left != null) { // 如果当前节点有左子节点
stack2.push(current.left); // 将左子节点压入栈中
}
}
}
5、在内部循环结束后,将postive的值取反,将stack2赋值给stack1,并将subList添加到list中。最后,当外部循环结束时,返回list作为结果。
postive = !postive; // 切换遍历方向
stack1 = stack2; // 将下一个栈赋值给当前栈
list.add(subList); // 将子列表添加到结果列表中
参考代码
以下代码用于实现二叉树的锯齿形层序遍历。它定义了一个名为TreeNode的类,表示二叉树的节点,以及一个名为Solution的类,其中包含一个名为zigzagLevelOrder的方法。该方法接受一个TreeNode类型的参数root,表示二叉树的根节点,并返回一个List<List<Integer>>类型的结果,表示锯齿形层序遍历的结果。
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> list = new LinkedList<>();
if (root == null) {
return list;
}
Stack<TreeNode> stack1 = new Stack<>();
stack1.push(root);
boolean postive = true;
while (!stack1.isEmpty()) {
Stack<TreeNode> stack2 = new Stack<>();
List<Integer> subList = new LinkedList<>();
while (!stack1.isEmpty()) {
TreeNode current = stack1.pop();
subList.add(current.val);
if (postive) {
if (current.left != null) {
stack2.push(current.left);
}
if (current.right != null) {
stack2.push(current.right);
}
} else {
if (current.right != null) {
stack2.push(current.right);
}
if (current.left != null) {
stack2.push(current.left);
}
}
}
postive = !postive;
stack1 = stack2;
list.add(subList);
}
return list;
}
}
解数独
题目
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
示例:
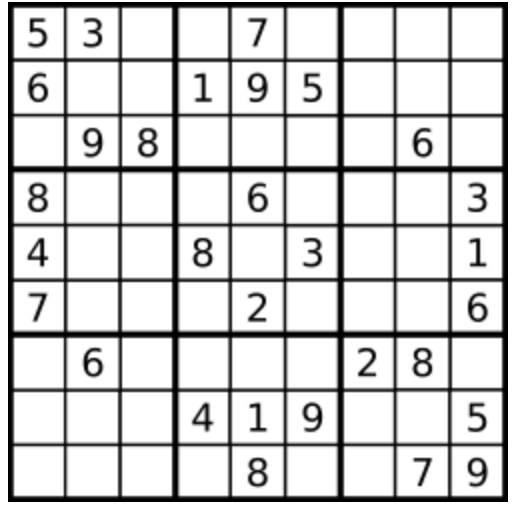
输入:board =
[[“5”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”],
[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”],
[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”],
[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”],
[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”],
[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”],
[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”],
[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”],
[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
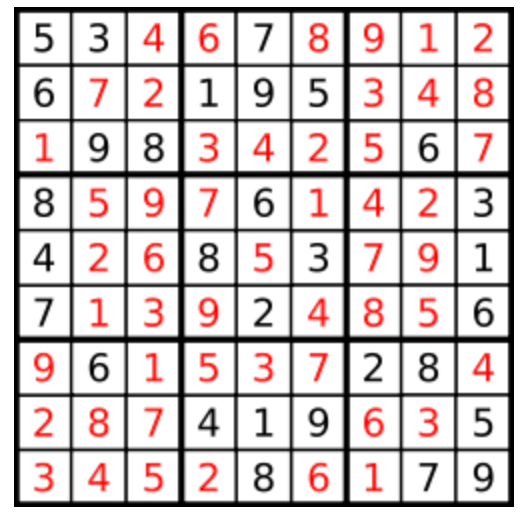
输出:
[[“5”,“3”,“4”,“6”,“7”,“8”,“9”,“1”,“2”],
[“6”,“7”,“2”,“1”,“9”,“5”,“3”,“4”,“8”],
[“1”,“9”,“8”,“3”,“4”,“2”,“5”,“6”,“7”],
[“8”,“5”,“9”,“7”,“6”,“1”,“4”,“2”,“3”],
[“4”,“2”,“6”,“8”,“5”,“3”,“7”,“9”,“1”],
[“7”,“1”,“3”,“9”,“2”,“4”,“8”,“5”,“6”],
[“9”,“6”,“1”,“5”,“3”,“7”,“2”,“8”,“4”],
[“2”,“8”,“7”,“4”,“1”,“9”,“6”,“3”,“5”],
[“3”,“4”,“5”,“2”,“8”,“6”,“1”,“7”,“9”]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:
提示:
board.length == 9
board[i].length == 9
board[i][j] 是一位数字或者 ‘.’
题目数据 保证 输入数独仅有一个解
解题思路
- 首先,我们需要遍历整个数独板,找到第一个空白格(用 ‘.’ 表示)。
- 然后,尝试在该空白格中填入数字 1-9。
- 对于每个填入的数字,检查其是否满足数独的规则。如果满足规则,继续下一步;否则,回溯到上一个空白格,尝试下一个数字。
- 如果当前数字无法满足数独规则,尝试下一个数字。
- 重复步骤 3-4,直到找到一个解或者遍历完所有可能的数字组合。
- 如果找到了一个解,返回该解;否则,返回空列表表示无解。
代码思路
思路如下:
-
首先,定义了三个布尔数组:
row、col和cell,用于记录每行、每列和每个3x3的小格子中的数字是否已经被使用过。// 定义三个布尔数组,分别表示行、列和3x3宫格是否已经填过数字 boolean row[][] = new boolean[9][9]; boolean col[][] = new boolean[9][9]; boolean cell[][][] = new boolean[3][3][9]; -
solveSudoku方法是主要的求解方法,它接受一个字符类型的二维数组board作为输入,表示数独的初始状态。再通过两层循环遍历整个数独板,将已经填入的数字对应的行、列和小格子标记为已使用。// 解决数独问题的主函数 public void solveSudoku(char[][] board) { // 遍历整个数独板,将已经填过的数字标记在对应的行、列和3x3宫格中 for (int i = 0; i < 9; i++) { for (int j = 0; j < 9; j++) { if (board[i][j] != '.') { int t = board[i][j] - '1'; row[i][t] = col[j][t] = cell[i / 3][j / 3][t] = true; } } } -
然后调用
dfs方法进行深度优先搜索,从左上角开始填充数独的空格。// 调用深度优先搜索算法进行求解 dfs(board, 0, 0); } -
dfs方法是一个递归函数,它接受当前位置的坐标(x, y)作为参数。// 深度优先搜索算法 public boolean dfs(char[][] board, int x, int y) { …… } -
如果当前位置已经到达了最后一列,则将行坐标加1,并将列坐标重置为0,继续处理下一行。
// 如果当前位置已经到达了数独板的最后一个位置,说明已经找到了一个解,返回true if (y == 9) { x++; y = 0; -
如果当前位置已经到达了最后一行,则返回
true表示数独已经成功解决。// 如果已经遍历完了整个数独板,说明找到了一个解,返回true if (x == 9) return true; -
如果当前位置已经有数字填入,则直接跳过该位置,继续下一个位置的处理。
// 如果当前位置已经有数字,直接跳过 if (board[x][y] != '.') return dfs(board, x, y + 1); -
对于空位置,遍历1到9的数字,检查该数字是否满足数独的规则。如果满足规则,则将该数字填入当前位置,并更新相应的行、列和小格子的标记。
// 尝试填入1-9中的一个数字,如果填入后仍然满足数独的规则,继续递归搜索下一个位置 for (int num = 0; num < 9; num++) { if (!row[x][num] && !col[y][num] && !cell[x / 3][y / 3][num]) { board[x][y] = (char) (num + '1'); row[x][num] = col[y][num] = cell[x / 3][y / 3][num] = true; -
递归调用
dfs方法,继续处理下一个位置。如果递归调用返回true,则说明找到了一个解,直接返回true。if (dfs(board, x, y + 1)) return true; -
如果遍历完所有可能的数字后仍然无法找到解决方案,则将当前位置的数字重置为’.',并取消相应的行、列和小格子的标记。
// 如果填入后仍然不满足数独的规则,回溯到上一个位置,尝试其他数字 board[x][y] = '.'; row[x][num] = col[y][num] = cell[x / 3][y / 3][num] = false; } } -
最后,如果遍历完所有可能的数字后仍然无法找到解决方案,则返回
false表示数独无解。
// 如果所有数字都尝试过了,仍然无法找到解,返回false
return false;
补充说明
什么是回溯算法?
回溯算法是一种选优搜索法,其核心思想是在搜索尝试过程中寻找问题的解。
当发现已不满足求解条件时,就**“回溯”返回,尝试别的路径**。更具体来说,它是一种类似枚举的搜索尝试过程,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回到上一步,重新选择。这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
需要注意的是,尽管回溯法可以解决许多问题,如组合问题、排列问题、切割问题、子集问题和棋盘问题等,但它并不是一种高效的算法。实际上,它更像是一种暴力搜索的方法,最多再剪枝一下。尽管如此,由于其在解决特定类型问题时的独特优势,回溯算法在编程和算法设计中仍然得到了广泛的应用。
参考代码
以下代码使用了回溯算法来填充数独的空格,并检查每个数字是否满足数独的规则。
class Solution {
boolean row[][] = new boolean[9][9];
boolean col[][] = new boolean[9][9];
boolean cell[][][] = new boolean[3][3][9];
public void solveSudoku(char[][] board) {
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] != '.') {
int t = board[i][j] - '1';
row[i][t] = col[j][t] = cell[i / 3][j / 3][t] = true;
}
}
}
dfs(board, 0, 0);
}
public boolean dfs(char[][] board, int x, int y) {
if (y == 9) {
x++;
y = 0;
}
if (x == 9)
return true;
if (board[x][y] != '.')
return dfs(board, x, y + 1);
for (int num = 0; num < 9; num++) {
if (!row[x][num] && !col[y][num] && !cell[x / 3][y / 3][num]) {
board[x][y] = (char) (num + '1');
row[x][num] = col[y][num] = cell[x / 3][y / 3][num] = true;
if (dfs(board, x, y + 1))
return true;
board[x][y] = '.';
row[x][num] = col[y][num] = cell[x / 3][y / 3][num] = false;
}
}
return false;
}
}