-
沟通:沟通渠道数=n(n-1)/2,n代表人数
-
风险
三角分布: 期望=[乐观 (小值) +最可能 (中值) +悲观 (大值) ]/3
贝塔分布:期望=[乐观(小值) +4*最可能(中值) +悲观(大值) ]/6
标准差=[悲观(大值)-乐观(小值) ]/6
方差=[悲观 (大值) -乐观 (小值) ]^2/36
概率计算: 士1标准差 概率 68%; 士2 标准差概率 95%; 士3 标准差概率 99%
-
成本
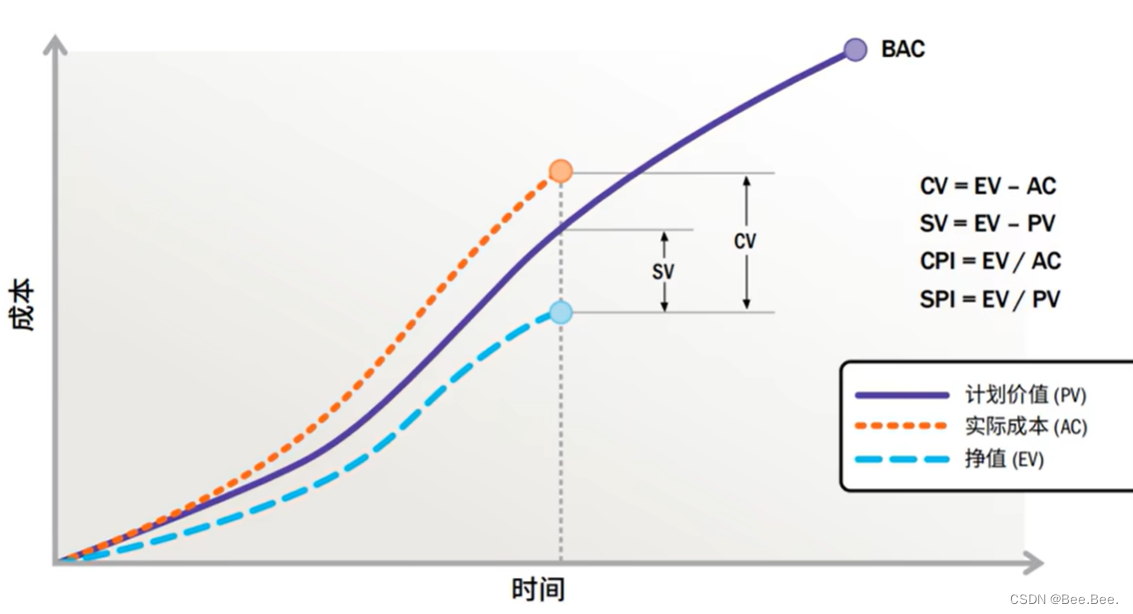
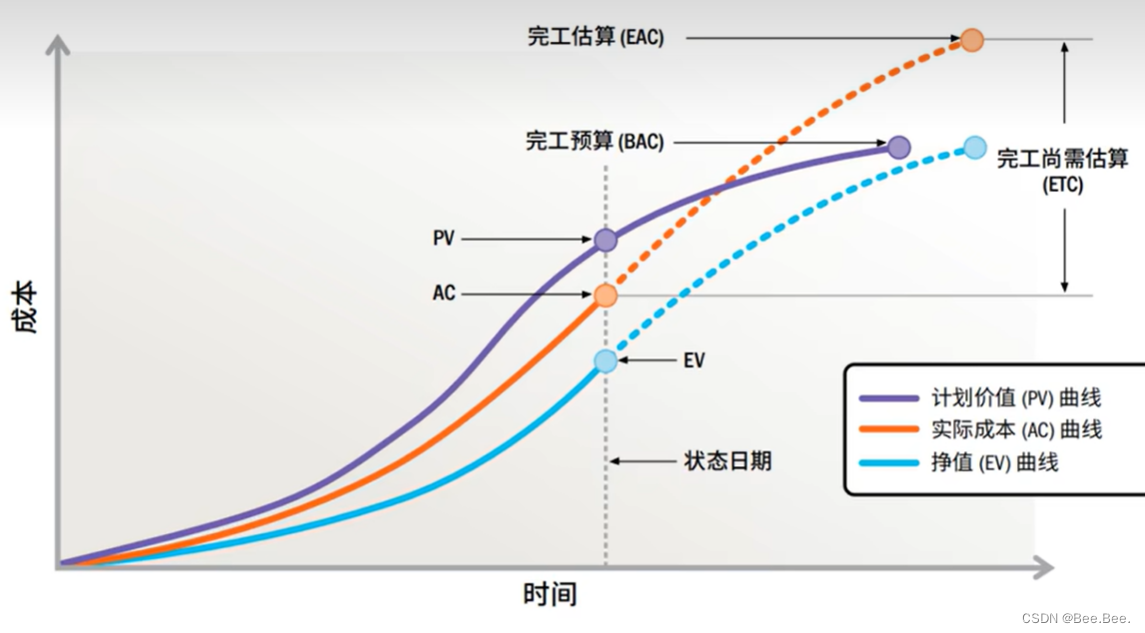
PV(计划价值):根据“监控点”看网络图
EV(挣值):EV=PV*SPI,计算时注意 SPI 是总计划价值还是当前计划价值的完成百分比
AC(实际成本):题目中一般会给出来
绩效情况: 根据 PV、EV、AC 计算进度偏差 SV、成本偏差 CV、进度绩效指数 SPI、成本绩效指数CPI,给出结论
项目总预算=成本基准(活动/工作成本估算 + 应急储备)+管理储备
活动成本估算=活动估算+活动应急储备。例:项目有 10 个活动,各活动的成本估算、应急储备分别是 2W、1W,项目的管理储备、应急储备分别是 5W、5W。(1) BAC=35W;(2) 成本基准=35W;(3) 项目总预算=40W
| 参描述数 | 公式 | 描述 |
|---|---|---|
| 成本偏差 CV | CV=EV-AC | >0,成本节支;<0,成本超支;=0,零偏差 |
| 进度偏差 SV | SV=EV-PV | >0,进度提前;<0,进度滞后;=0,零偏差 |
| 成本绩效指数 CPI | CPI=EV/AC | >1,成本节支;<1,成本超支;=1,零偏差 |
| 进度绩效指数 SPI | SPI=EV/PV | >1,进度提前;<1,进度滞后;=1,零偏差 |
| 完工尚需估算 ETC | 非典型:ETC=BAC-EV;典型: ETC=(BAC-EV)/CPI, | 非典型: 知错就改不再偏差;典型: 死不悔改继续偏差,一般 CPI<1 |
| 完工估算 EAC | EAC=AC+ETC | 非典型: EAC=AC+(BAC-EV);典型: EAC=AC+ (BAC-EV) /CPI=BAC/CPI |
| 完工偏差 VAC | VAC=BAC-EAC | >0,项目节支;<0,项目超支;=0,项目无偏差 |
| 完工预算 BAC | BAC=PV 之和 | 完工预算=成本基准=BAC,不含管理储备 |
| TCPI | 预算内=(BAC-EV)/(BAC-AC);预算失效=(BAC-EV)/(EAC-AC) | >1,很难完成;<1,很容易完成 |
-
-
-
进度
| ES: 最早开始时间 | DU: 工作历时/工期 | EF: 最早完成时间,EF=ES+工期 |
|---|---|---|
| ID (工作代号) | ||
| LS:最迟开始时间 | TF:总浮动时间,TF=LS-ES=LF-EF | LF: 最迟完成时间,LF=LS+工期 |
-
总体原则:正向取大、反向取小
-
时间六标识具体步骤
-
正向取大,计算并标记早参数 (最早开始时间、最早完成时间)
-
反向取小,计算并标记晚参数 (最迟开始时间、最迟完成时间)
-
尾活动的最早完成和最晚完成即为活动总工期
-
计算并标记总时差,总时差= (最晚完成 - 最早完成)本活动
-
粗线或双实线标记连线总时差为 0 的活动,此线路即为关键路径(可能有多条,验证)
-
进度标号法具体步骤(快速计算总工期、关键路径、自由浮动时间、总浮动时间)
-
从首活动正向开始逐个标记每个代号的工作历时
-
正向取大,选择后在小的线路上画波浪线,波浪线处大值-小值标记
-
总工期:最后一个代号的标记值
-
关键路径: 从尾活动逆向不出现波浪线的线路
-
自由时差: 本活动的波浪线 如无则为 0,0 和波浪线之间取小值 0
-
总时差: 本活动自由时差+后续所有线路的最小值
-
工期判断:判断是否为关键活动
若关键活动延误,工期必会影响,关键路径可能变化,需要重新计算
若非关键活动延误,看延误工期是否在可控的总浮动时间以内。若未大于总浮动时间,则不影响工期;若大于总浮动时间,总工期=实际工期+ (延误工期-总浮动时间)
若进度压缩工期 1天,只看关键路径关键活动;若进度压缩工期>=2 天,则必须列出所有路径进行判断