自动驾驶算法（五）：基于遗传算法的路径规划（上）

1 遗传算法介绍

2 遗传算法代码详解--绘制地图与种群初始化代码讲解

1 遗传算法介绍

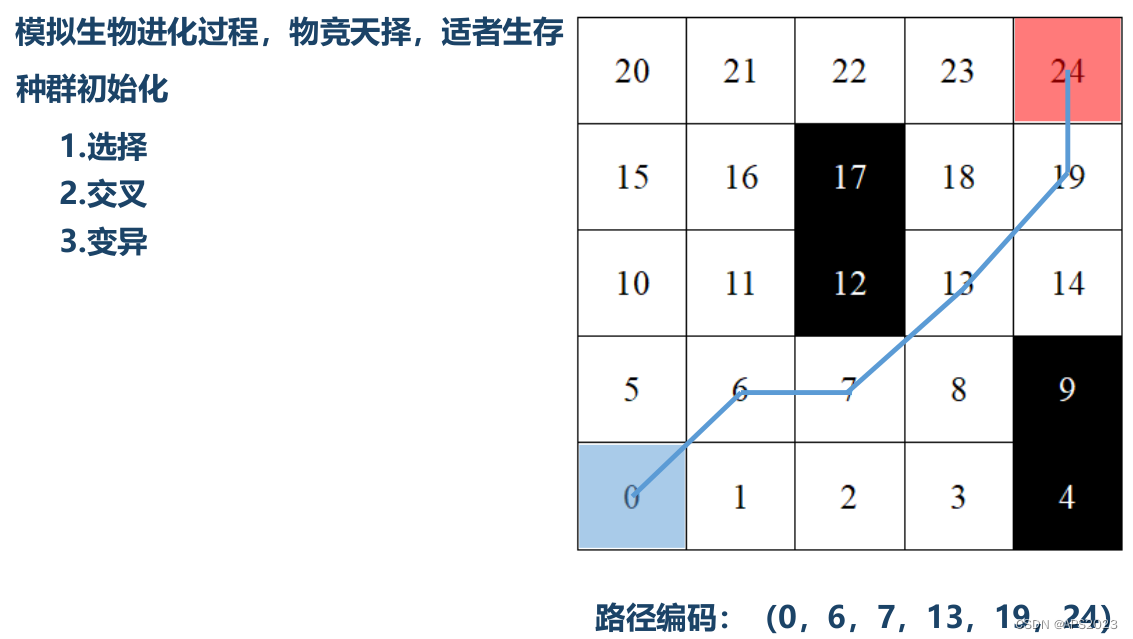
        模拟生物进化过程，物竞天择，适者生存。

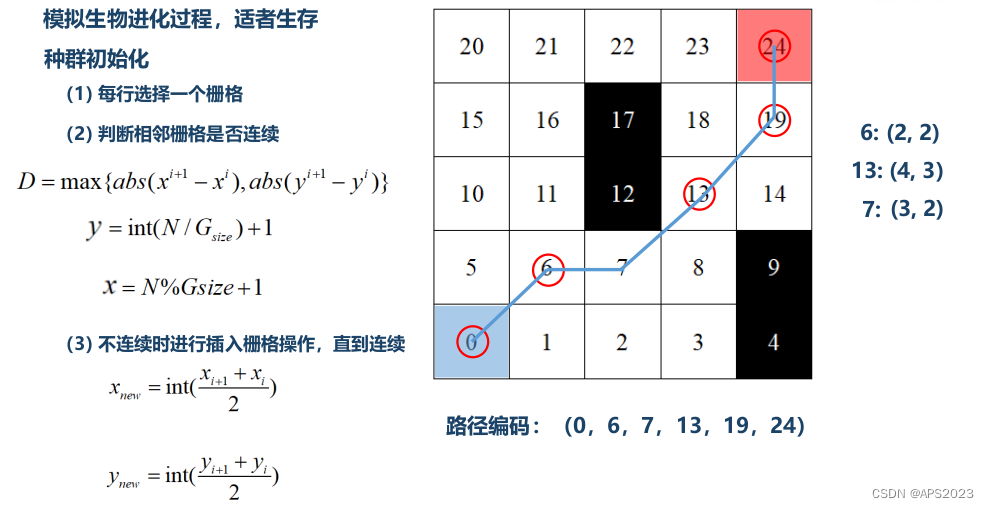
        我们先为栅格地图进行编码：从起点0出发到终点24这个栅格。我们首先有一条路径（0，6，7，13，19，24），我们用这个方法表示一个个体，我们首先要产生很多这样的个体。这就是种群初始化的过程：

        1.我们发现每行至少要选择一个栅格，因此我们要每行选择一个栅格，起点要选择，第二行选择6，第三行选择13，第四行选择19，第五行选择24（终点）。

        2.判断相邻的栅格是否连续（是否可以一步走过去）（为地图建立一个坐标系，为每个栅格分配一个(X,Y)坐标。）如果两个栅格的最大X，Y的坐标差小于等于1是可以走过来的。（表示两个栅格是对角的或者相邻的）

        3.如果发现两个栅格不连续进行插入栅格方式，直到连续（6号与13号不连续），插入7号再判断2。如果有碰撞的话会有更复杂的操作，这个我们会接下来说。

        比如6号栅格的坐标为(2,2)，13号栅格为(4,3)，我们取中间的栅格(3,2)（7号栅格）

        总体流程如下：

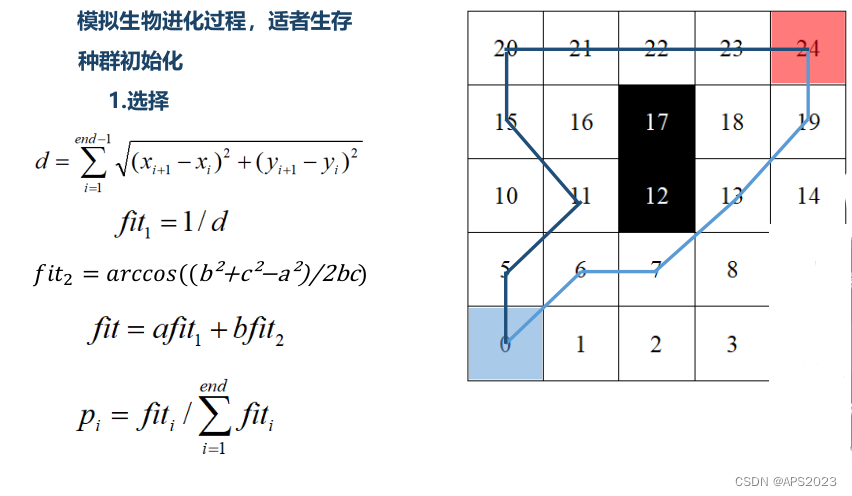
        种群初始化就是产生出很多条这样的路径，在初始化以后，我们就要进入遗传算法的循环了，首先第一步就是选择，如下图：

        我们有两条路径对应两个个体，我们要选择较好的个体，选择标准可以是路径的长度d，我们选择路径的倒数为适应度，越短的路径它的适应度就越大。还有就是路径的顺滑性，以相邻的三个点为例子，会组成一个三角形，我们就希望三个点连起来的角度越大，我们可以通过余弦定理来得到加入适应度函数。我们根据经验计算每个适应度的权重a，b，这个通过经验或者实验获得。我们有了每条路径的适应度的值，我们会对每个个体计算保留的概率pi。

        第二步就是交叉，如下图：

        上图中的两条路经在13号点出现了交叉，我们可以交换交叉点前后的路径生成两条新的路径，这样就丰富了个体。

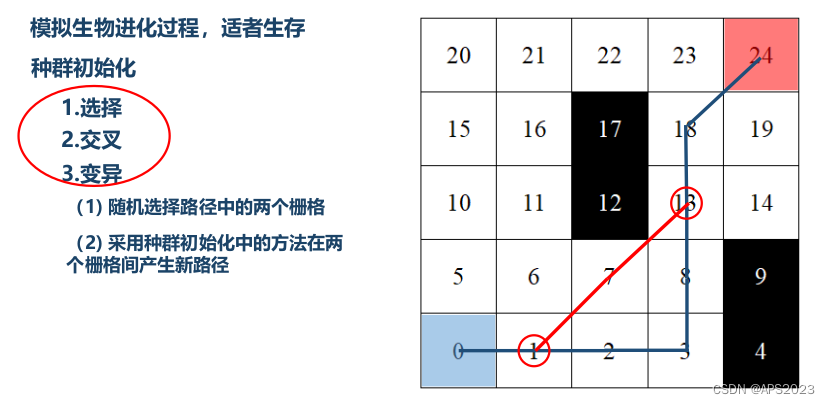
        第三步就是变异，如下图：

        我们先随机的在路径中选择两个栅格（在这里我们选择1、13号栅格），采用种群初始化的方式在两个栅格间产生新的路径（比如1、7、13），我们循环执行这三步。每次选择更好的路径保存下来再通过交叉变异产生新的路径，整个种群都会向着更好的方向发展

2 遗传算法代码详解--绘制地图与种群初始化代码讲解

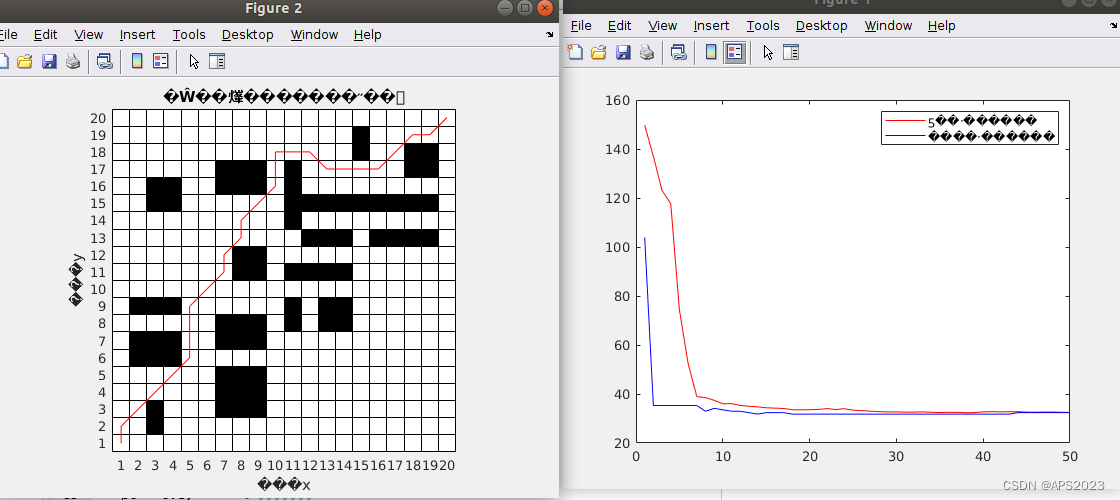
先看一下运行效果：

看下代码，我们首先绘制地图：

clc;
clear;
% Grid Map
G=  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
     0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
     0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
     0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 1 1 1 0 1 0 1 1 0 0 0 0 0 0;
     0 1 1 1 0 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0;
     0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 0 1 1 0 1 1 1 1 0 0 0 0 0 0;
     0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0;
     0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0;
     0 0 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0;
     0 0 1 1 0 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 1 1 1 0 1 0 0 0 0 0 0 1 1 0; 
     0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0;
     0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0;
     0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0];

注意，这是反过来的！！！！我们第一行是图形的最下面。

随后我们初始化了一些变量：

p_start = 0;   % 开始的index
p_end = 399;   % 结束的index
NP = 200;      % 种群大小
max_gen = 50;  % 最大进化次数
pc = 0.8;      % 交叉处理频率
pm = 0.2;      % 变异频率
init_path = [];
z = 1;  
new_pop1 = {}; % 路径
[y, x] = size(G);  % 地图的x和y的数量 x=y=20
% x的起点 p_start对应开始的栅格
% xs = 1  ys = 1
% 举个例子  p_start 的值是 10，x 的值是 3，那么表达式的计算过程如下 mod(10, 3) + 1 = 1+1 = 2
xs = mod(p_start, x) + 1; 
% y的起点 p_start对应开始的栅格
% 如果 p_start 的值是 10，x 的值是 3，那么表达式的计算过程如下 fix(10 / 3) + 1 = fix(3.333333) + 1 = 3+1=4 
ys = fix(p_start / x) + 1;

% x、y的终点栅格坐标 
% mod(399,20) + 1 = 19 + 1 = 20
% fix(399/20) + 1 = 19 + 1 = 20
xe = mod(p_end, x) + 1;
ye = fix(p_end / x) + 1;

% step1 种群初始化
% pass_num 20 - 20 + 1 = 1
pass_num = ye - ys + 1;

% 种群有NP = 200个个体 每个个体的路径个数初始化为起点到终点的y距离(好像是不太够呀) 
pop = zeros(NP, pass_num);

我们在下面这段代码进行种群初始化：

% 种群初始化代码
for i = 1 : NP
    % 无论是哪一条路径 起点肯定是起点 pop(1,:)存储的是第一个种群 pop(1,1)就是第一个种群的读一个节点
    pop(i, 1) = p_start;
    j = 1;
    % yk = 2 : 19  遍历每一个路径的每一行
    % 更新pop(1,1) pop(1,2) ... pop(1,20)
    for yk = ys+1 : ye-1
        j = j + 1;
        % 存储一行的可行点
        can = []; 
        % xk = 1 : 20
        for xk = 1 : x
            % 栅格编号 没有障碍物
            no = (xk - 1) + (yk - 1) * x;
            if G(yk, xk) == 0
                % 将变量 no 添加到数组 can 的末尾。
                can = [can no];
            end
        end
        can_num = length(can);
        % 产生随机整数
        index = randi(can_num);
        % 为每一行添加一个可行点 can存储着一行的可行点  can(index)
        pop(i, j) = can(index);
    end
    pop(i, end) = p_end;
    % pop
    % 将上述必经节点联结成无间断路径
    single_new_pop = generate_continuous_path(pop(i, :), G, x);
    % init_path = [init_path, single_new_pop];
    if ~isempty(single_new_pop)
       new_pop1(z, 1) = {single_new_pop};
        z = z + 1;
    end
end

我们拿第一个种群的生成举例子吧：

pop被我们初始化为zeros(NP, pass_num); 也就是200*20的空矩阵，也就是每一列存储着一个种群的路径。也就是：pop(1,1) pop(2,1).....pop(20,1)存储着第一个种群的信息。那么第一个种群的起始点一定是我们导航的初始坐标pop(1,1) = start，然后我们更新第2-19列的值，先看第一个for循环，我们把每一行的可行点（除去障碍物点的点都加入了can列表中，我们随机生成一个和列表长度相同的索引将这个索引代表的点作为这一行的路径）

但是这些路径未必连通，我们需要将路径连通，我们用generate_continuous_path函数去保证路径连通：

% 传入参数 个体的路径 地图 一行有多少个元素x
% 它告诉 MATLAB 这是一个名为 generate_continuous_path 的函数，它接受三个输入参数 single_pop，G 和 x，并且它会返回一个名为 single_new_pop 的变量。
function [single_new_pop] = generate_continuous_path(single_pop, G, x)
i = 1;
single_new_pop = single_pop;
% 这行代码调用了 size 函数来获取变量 single_new_pop 的大小，并将结果存储在了 single_path_num 变量中。
% 在这里，使用了波浪线 ~ 来表示忽略了 size 函数返回的第一个值（也就是行数），只保留了列数。
% single_new_pop 是一个 1 * 20的向量
% single_path_num
[~, single_path_num] = size(single_new_pop);

% 遍历每一列 1-20
while i ~= single_path_num
    % 点i所在列 (从左到右编号)
    x_now = mod(single_new_pop(1, i), x) + 1; 
    % 点i所在行 (从上到下编号)
    y_now = fix(single_new_pop(1, i) / x) + 1;
    % 点i+1所在行 (从上到下编号)
    x_next = mod(single_new_pop(1, i + 1), x) + 1;
    y_next = fix(single_new_pop(1, i + 1) / x) + 1;
    
    % 初始化最大迭代次数
    max_iteration = 0;
    
    % 如果他们不相连的话
    while max(abs(x_next - x_now), abs(y_next - y_now)) > 1
        x_insert = floor((x_next + x_now) / 2);
        y_insert = floor((y_next + y_now) / 2);
        
        % 取得两者中点值
        if G(y_insert, x_insert) == 0  
            % 栅格值
            num_insert = (x_insert - 1) + (y_insert - 1) * x;
            % single_new_pop 是一个数组，这段代码的目的是将 num_insert 插入到 single_new_pop 的第 i 个位置之后。
            % single_new_pop(1, 1:i) 表示取 single_new_pop 中第1行，从第1列到第i列的元素。
            % single_new_pop(1, i+1:end) 表示取 single_new_pop 中第1行，从第i+1列到最后一列的元素。
            single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];
            
        % 如果是障碍物的话
        else   
            % 它检查该点左面是否有路径 
            % (x_insert - 2) + (y_insert - 1) * x 是否不等于 single_new_pop(1, i)。
            if G(y_insert, x_insert - 1) == 0 && ((x_insert - 2) + (y_insert - 1) * x ~= single_new_pop(1, i)) && ((x_insert - 2) + (y_insert - 1) * x ~= single_new_pop(1, i+1))
                x_insert = x_insert - 1;
                % 索引号
                num_insert = (x_insert - 1) + (y_insert - 1) * x;
                % 插入
                single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];
                               
            elseif G(y_insert, x_insert + 1) == 0 && (x_insert + (y_insert - 1) * x ~= single_new_pop(1, i)) && (x_insert + (y_insert - 1) * x ~= single_new_pop(1, i+1))
                x_insert = x_insert + 1;
                num_insert = (x_insert - 1) + (y_insert - 1) * x;
                single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];
                
            elseif G(y_insert + 1, x_insert) == 0 && ((x_insert - 1) + y_insert * x ~= single_new_pop(1, i)) && ((x_insert - 1) + y_insert * x ~= single_new_pop(1, i+1))
                y_insert = y_insert + 1;
                num_insert = (x_insert - 1) + (y_insert - 1) * x;
                single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];

            elseif  G(y_insert - 1, x_insert) == 0 && ((x_insert - 1) + (y_insert - 2) * x ~= single_new_pop(1, i)) && ((x_insert - 1) + (y_insert-2) * x ~= single_new_pop(1, i+1))
                y_insert = y_insert - 1;
                num_insert = (x_insert - 1) + (y_insert - 1) * x;
                single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];
                
            % 左右上下都是占据的则删去路径
            else
                %break_pop = single_new_pop
                single_new_pop = [];
                break
            end    
        end
        
        x_next = x_insert;
        y_next = y_insert;
        max_iteration = max_iteration + 1;
        if max_iteration > 20000
            single_new_pop = [];
            break
        end
        
    end
    
    if isempty(single_new_pop)
        break
    end
    
    [~, single_path_num] = size(single_new_pop);
    i = i + 1;
end

到此为止，我们已经完成了种群初始化环节，规划出了很多条路径。