本文建立在上一篇文章的基础上:《十种排序算法(1) - 准备工具》
注:本文以升序为例子进行实现和解释
1.选择排序
选择排序是最简单几种排序算法之一
(1) 原理
不断使用查找并选择最小的元素放到数组的首端
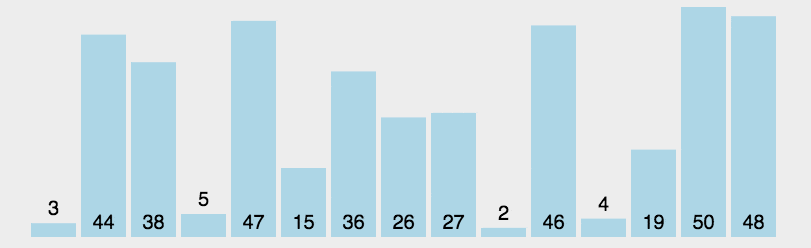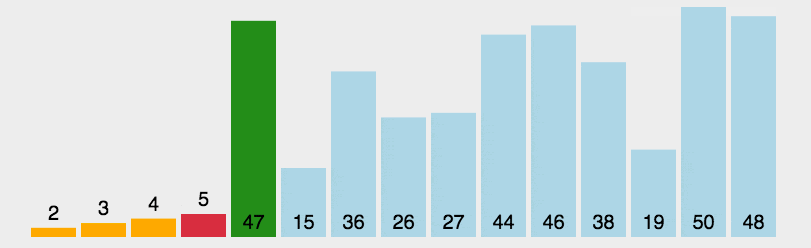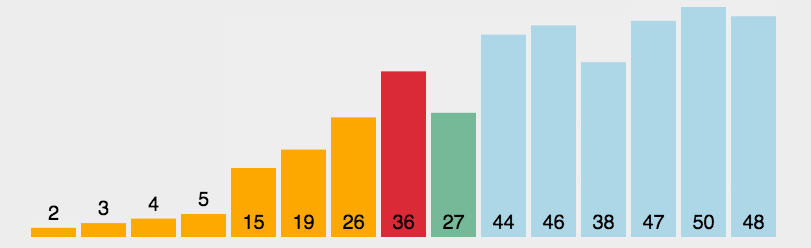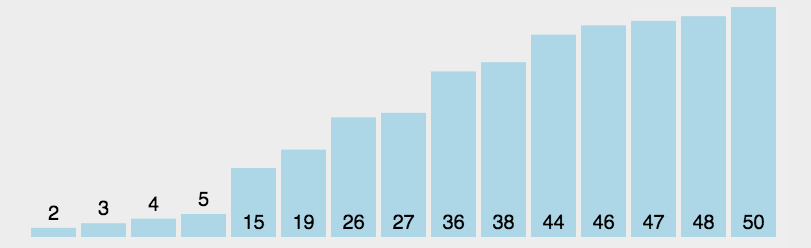
(2) 复杂度分析
- 最好:O(n^2)
- 最坏:O(n^2)
- 平均:O(n^2)
- 空间复杂度:O(1)
- 稳定:否
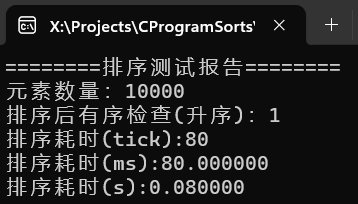
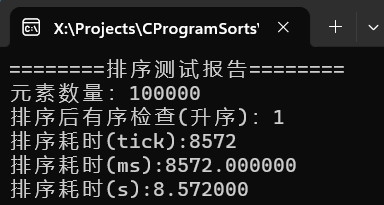
(3) 实现
//选择排序 O(n^2)
inline void selectionSort(int* nums, int numsSize)
{
for (int i = 0; i < numsSize - 1; i++)
{
int minIndex = i;
for (int a = i ; a < numsSize; a++)
{
minIndex = nums[a] < nums[minIndex] ? a : minIndex;
}
if (minIndex != i) swap(&nums[i], &nums[minIndex]);
}
}
2.冒泡排序
冒泡排序是最简单的几种排序算法之一
(1) 原理
重复遍历数组,每次都比较nums[i]和nums[i+1]的大小,如果前者大于后者则交换,如果此次遍历无交换,可以立刻结束排序过程。
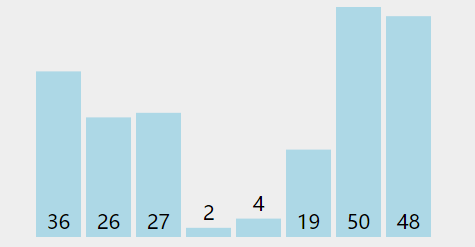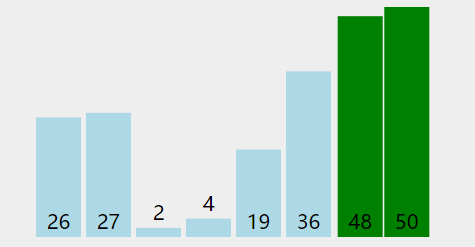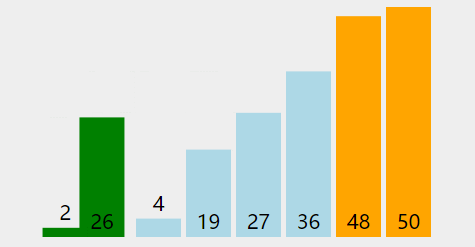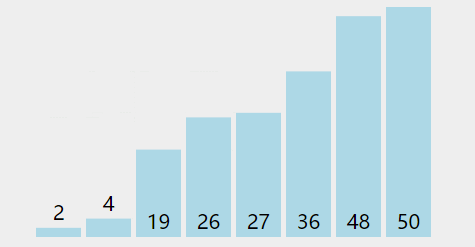
形象的理解可以理解成气泡在水中冒出的过程。
(2) 复杂度分析
- 最好:O(n) - 当数组本身已经是排序好的状态时,冒泡排序只需要进行一轮遍历即可确认数组有序
- 最坏:O(n^2) - 当数组是逆序排列时,冒泡排序需要进行最大数量级的比较和交换。
- 平均:O(n^2)
- 空间复杂度:O(1)
- 稳定:是
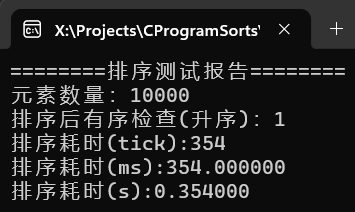
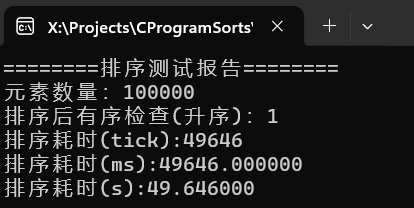
可以看到冒泡排序的时间复杂度与选择排序相同,但是时间差距巨大。主要原因是操作类型的不同,选择排序有更少的交换次数。而比较次数上,二者相差不大,
冒泡排序往往在数据本身就大部分有序的时候有良好的表现,其耗时取决于数据本身的逆序度,而本测试程序取随机值,数据无序度一般相当高。冒泡排序在数据完全有序时仅为O(n),而在数据完全逆序时,退化为O(n2)
(3)实现
inline void bubbleSort(int* nums, int numsSize)
{
//i为有序元素个数
for (int i = 0; i < numsSize - 2; i++)
{
int swapCount = 0;
for (int x = 0; x < numsSize - i - 1; x++)
{
if (nums[x] > nums[x + 1])
{
swap(&nums[x], &nums[x + 1]);

swapCount++;
}
}
if (!swapCount) break;
}
}
3.直接插入排序
(1)原理
遍历数组,在当前元素之前(认为之前已经有序)找到合适的位置进行插入。
(2)复杂度分析
- 最好:O(n) - 当数组本身已经是基本有序时,插入排序只需要进行少量的比较和移动
- 最坏:O(n^2) - 当数组是逆序排列时,插入排序需要进行最大数量级的比较和移动。
- 平均:O(n^2)
- 空间复杂度:O(1)
- 稳定:是
插入排序同样是在部分有序时表现很好
4.希尔排序
(1)原理
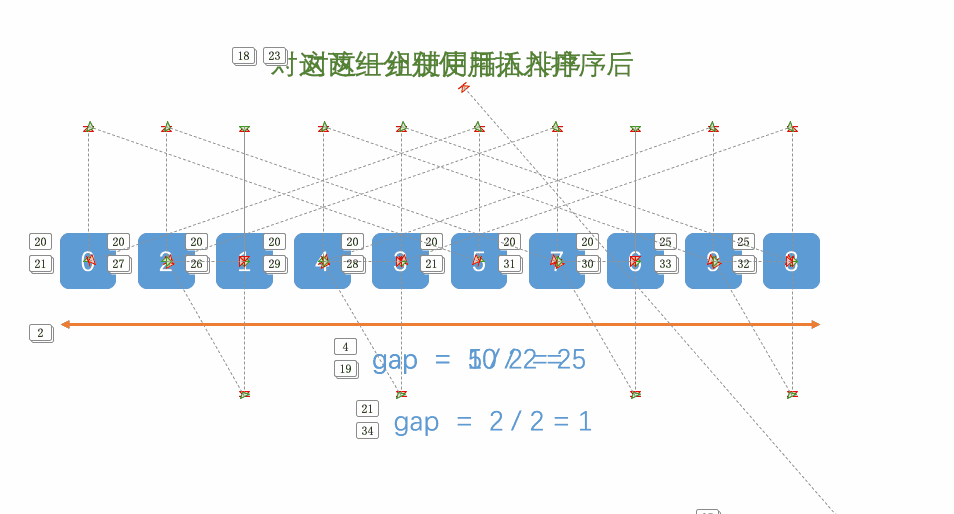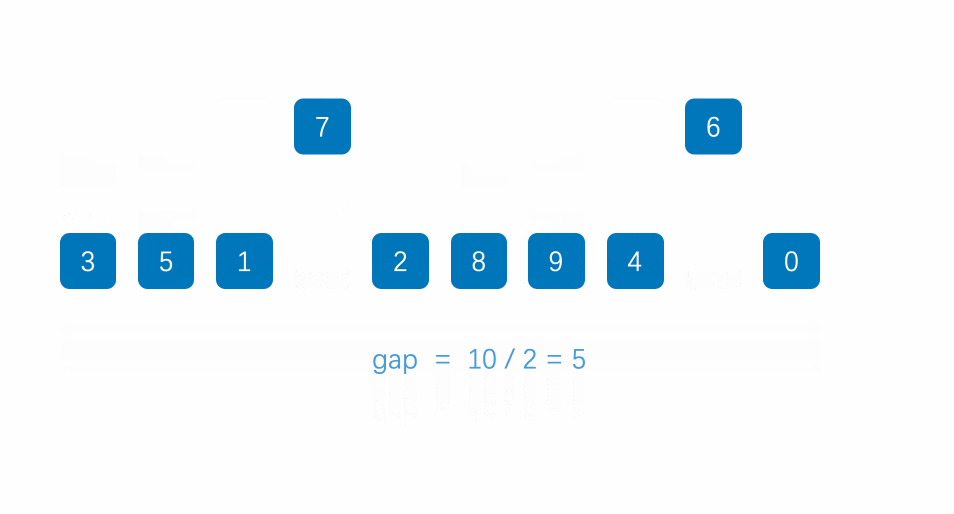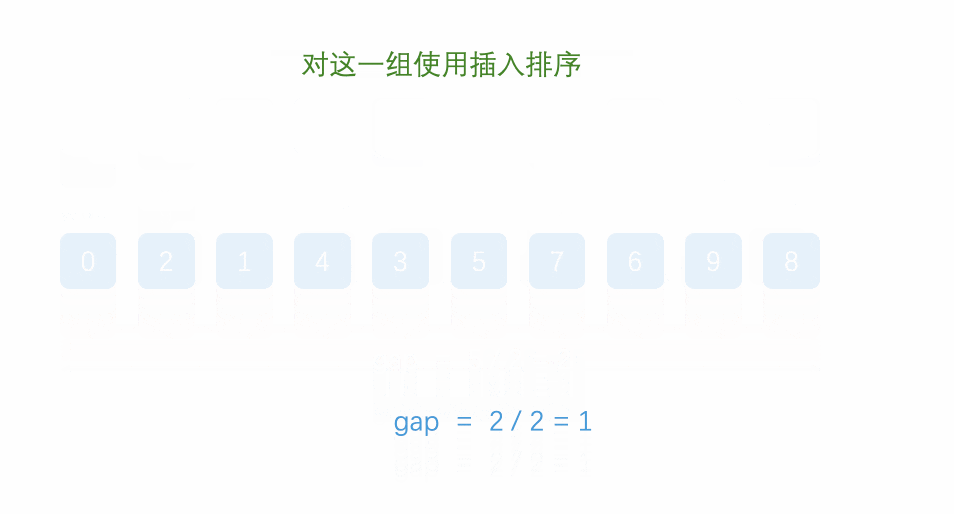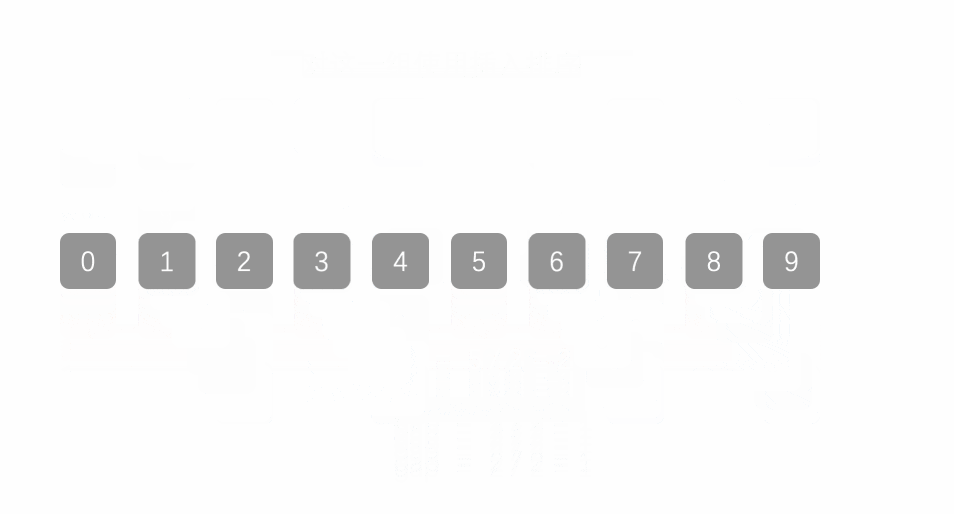
希尔排序是对插入排序的优化,是一个多阶段排序算法,它通过改变增量序列,对数据进行多轮排序,逐渐减少增量,最终完成排序。由于最开始的排序阶段会进行远距离的交换,因此可以更快地消除逆序对,使得后续的插入排序阶段所需的移动次数大大减少。
希尔建议的增量为 numSize / (2n),但是这并非最优解,根据数据规模和规律的不同选取不同的增量会有更佳的效果,可以根据使用情景查阅。
(2)复杂度分析
- 最好:取决于增量序列的选择,通常为 O(n log^2 n) 或更好
- 最坏:O(n^2)
- 平均:取决于增量序列的选择,通常为 O(n log^2 n) 或更好
- 空间复杂度:O(1)
- 稳定:否
(3)实现
//希尔排序
inline void shellSort(int* nums, int numsSize)
{
int gap = 1;
while (gap <= numsSize / 3)
gap = gap * 3 + 1; // 使用 Knuth 增量序列
while (gap > 0)
{
for (int i = gap; i < numsSize; ++i)
{
int temp = nums[i];
int j;
for (j = i; j >= gap && nums[j - gap] > temp; j -= gap)
nums[j] = nums[j - gap];
nums[j] = temp;
}
gap = (gap - 1) / 3; // 逆序列
}
}
5.快速排序
快速排序的特点是非常快!!非常快,尤其是数据规模大的时候。

快速排序是一种分治算法,其基本思想是选择一个基准值(pivot),通过对数组进行分区操作,将数组分成两个子数组,其中左边的子数组中的元素小于等于基准值,右边的子数组中的元素大于基准值,然后递归地对子数组进行排序。这个过程不断重复,直到整个数组有序。
谨记:
- 基准值尽量是中位数,可以随便选
- 左右指针可以放数组两边,逐渐相互靠近
- 交换左右指针所指元素来实现一边大一边小
- 对产生的俩数组再进行快排
(3)复杂度分析
- 最优时间复杂度:O(n log n)
- 最差时间复杂度:O(n^2)
- 平均时间复杂度:O(n log n)
- 空间复杂度:O(log n) 到 O(n) - 取决于递归深度
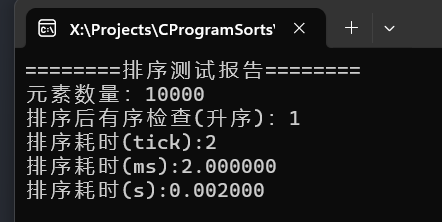
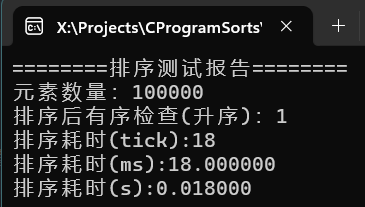
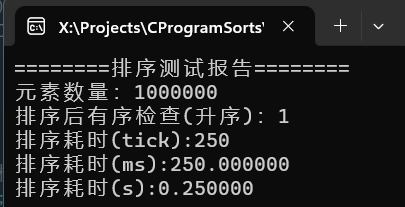
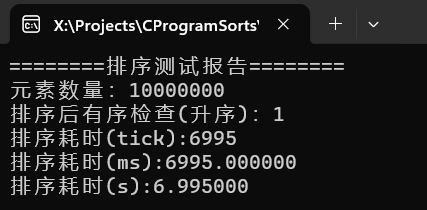
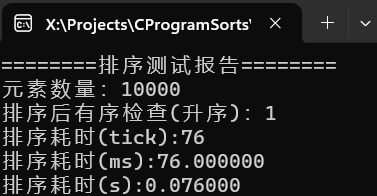
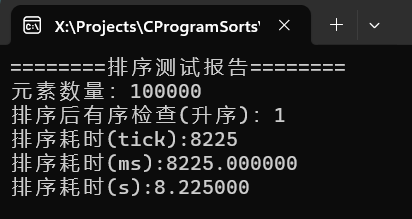
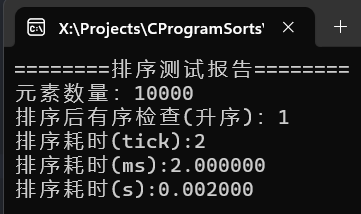
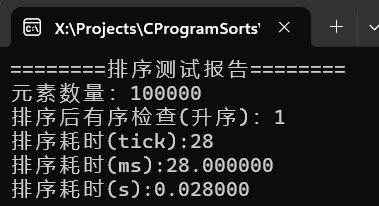
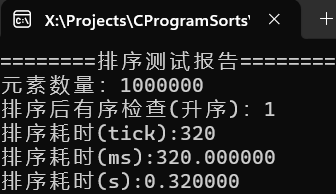
可以看到千万级别的随机数据,耗时7秒,百万级甚至不足一秒
(3)实现
递归实现(数据量过大会爆栈)
inline void quickSort(int* nums, int numsSize)
{
if (numsSize <= 1) return;
//快排基准
int pivot = nums[0];
//左右索引分别位于数组两侧
int left = 0;
int right = numsSize - 1;
//交替移动左右索引
while (left < right)
{
//Right
while (left < right)
{
if (nums[right] <= pivot)
{
swap(&nums[left], &nums[right]);
break;
}
else right--;
}
//Left
while (left < right)
{
if (nums[left] > pivot)
{
swap(&nums[left], &nums[right]);
break;
}
else left++;
}
}
//基准复位
nums[left] = pivot;
//递归
//part1 (index): 0 - left
quickSort(nums, left);
//part2(index) : (left+1) - (numsSize-left-1)
quickSort(&nums[left + 1], numsSize - 1 - left);
}
非递归实现
inline void quickSort(int* nums, int numsSize)
{
if (numsSize <= 1) return;
// 创建一个栈来模拟递归调用
int* stack = (int*)malloc(numsSize * sizeof(int));
if (stack == NULL) {
// 错误处理,内存分配失败
return;
}
int top = -1;
stack[++top] = 0; // 入栈左边界
stack[++top] = numsSize - 1; // 入栈右边界
while (top >= 0) {
// 出栈右边界和左边界
int right = stack[top--];
int left = stack[top--];
// 划分区间
int pivot = nums[left];
int l = left, r = right;
while (l < r) {
while (l < r && nums[r] >= pivot) r--;
if (l < r) nums[l++] = nums[r];
while (l < r && nums[l] <= pivot) l++;
if (l < r) nums[r--] = nums[l];
}
nums[l] = pivot;
// 对左右子数组进行入栈排序
if (left < l - 1) {
stack[++top] = left;
stack[++top] = l - 1;
}
if (right > l + 1) {
stack[++top] = l + 1;
stack[++top] = right;
}
}
free(stack); // 释放动态分配的栈内存
}
今天写到这hh,其他的代码去年也写过了,只是文没写完,写一遍复习这文当就笔记了