算法原理

桶排序

核心思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

计数排序：
计数排序其实是桶排序的一种特殊情况。当要排序的 n 个数据，所处的范围并不大的时候，比如最大值是 k，我们就可以把数据划分成 k 个桶。那我们如何快速计算出，每个值的在有序数组中对应的存储位置呢？

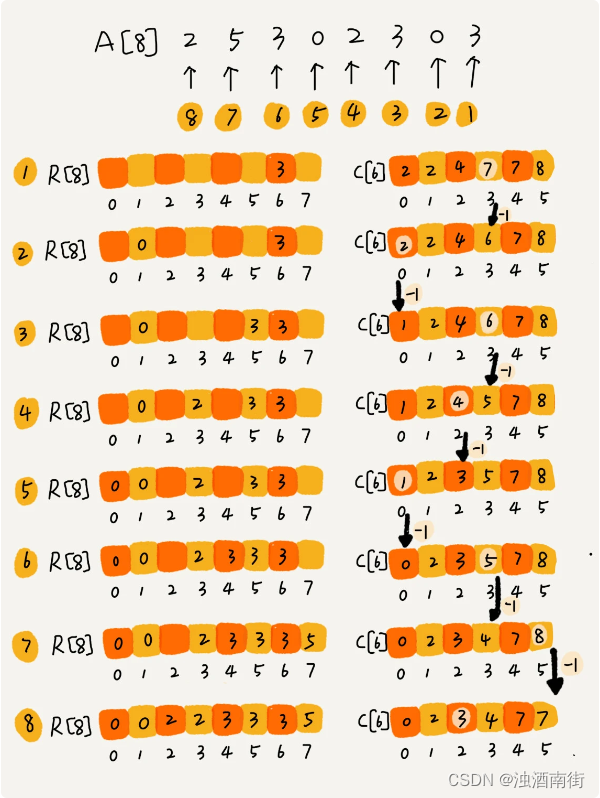
代码实现

桶排序代码实现

package com.athome.sort;

public class BucketSort {
    public static void main(String[] args) {
        int[] arr = new int[]{6, 11, 3,10, 9,7, 8,2,15,19,4,5,20};
        bucketSort(arr,3);

        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i]+ " ");
        }

    }
    public static void bucketSort(int[] arr, int bucketSize) {
        if (arr.length < 2) {
            return;
        }

        // 数组最小值
        int minValue = arr[0];
        // 数组最大值
        int maxValue = arr[1];
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] < minValue) {
                minValue = arr[i];
            } else if (arr[i] > maxValue) {
                maxValue = arr[i];
            }
        }

        // 桶数量
        int bucketCount = (maxValue - minValue) / bucketSize + 1;
        int[][] buckets = new int[bucketCount][bucketSize];
        int[] indexArr = new int[bucketCount];

        // 将数组中值分配到各个桶里
        for (int i = 0; i < arr.length; i++) {
            int bucketIndex = (arr[i] - minValue) / bucketSize;
            if (indexArr[bucketIndex] == buckets[bucketIndex].length) {
                ensureCapacity(buckets, bucketIndex);
            }
            buckets[bucketIndex][indexArr[bucketIndex]++] = arr[i];
        }

        // 对每个桶进行排序，这里使用了快速排序
        int k = 0;
        for (int i = 0; i < buckets.length; i++) {
            if (indexArr[i] == 0) {
                continue;
            }
            quickSortC(buckets[i], 0, indexArr[i] - 1);
            for (int j = 0; j < indexArr[i]; j++) {
                arr[k++] = buckets[i][j];
            }
        }
    }

    /**
     * 数组扩容
     *
     * @param buckets
     * @param bucketIndex
     */
    private static void ensureCapacity(int[][] buckets, int bucketIndex) {
        int[] tempArr = buckets[bucketIndex];
        int[] newArr = new int[tempArr.length * 2];
        for (int j = 0; j < tempArr.length; j++) {
            newArr[j] = tempArr[j];
        }
        buckets[bucketIndex] = newArr;
    }

    /**
     * 快速排序递归函数
     *
     * @param arr
     * @param p
     * @param r
     */
    private static void quickSortC(int[] arr, int p, int r) {
        if (p >= r) {
            return;
        }

        int q = partition(arr, p, r);
        quickSortC(arr, p, q - 1);
        quickSortC(arr, q + 1, r);
    }

    /**
     * 分区函数
     *
     * @param arr
     * @param p
     * @param r
     * @return 分区点位置
     */
    private static int partition(int[] arr, int p, int r) {
        int pivot = arr[r];
        int i = p;
        for (int j = p; j < r; j++) {
            if (arr[j] <= pivot) {
                swap(arr, i, j);
                i++;
            }
        }

        swap(arr, i, r);
        return i;
    }

    /**
     * 交换
     *
     * @param arr
     * @param i
     * @param j
     */
    private static void swap(int[] arr, int i, int j) {
        if (i == j) {
            return;
        }

        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

计数排序代码实现

package com.athome.sort;

public class CountSort {
    public static void main(String[] args) {
        int[] arr = new int[]{6, 11, 3,10, 9,7, 8,2,15,19,4,5,20};
        countingSort(arr,13);

        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i]+ " ");
        }

    }
    // 计数排序，a是数组，n是数组大小。假设数组中存储的都是非负整数。
    public static void countingSort(int[] a, int n) {
        if (n <= 1) return;

        // 查找数组中数据的范围，是为了确定数组c的长度
        int max = a[0];
        for (int i = 1; i < n; ++i) {
            if (max < a[i]) {
                max = a[i];
            }
        }

        // 申请一个计数数组c，下标大小[0,max]
        int[] c = new int[max + 1];

        // 计算每个元素的个数，放入c中
        for (int i = 0; i < n; ++i) {
            c[a[i]]++;
        }

        // 依次累加
        for (int i = 1; i < max + 1; ++i) {
            c[i] = c[i-1] + c[i];
        }

        // 临时数组r，存储排序之后的结果
        int[] r = new int[n];
        // 计算排序的关键步骤了，有点难理解
        for (int i = n - 1; i >= 0; --i) {
            int index = c[a[i]]-1;
            r[index] = a[i];
            c[a[i]]--;
        }

        // 将结果拷贝会a数组
        for (int i = 0; i < n; ++i) {
            a[i] = r[i];
        }
    }
}