from itertools import count
from collections import Counter
from heapq import heapify, heappush, heappop

def huffman_tree(s):
    # 统计每个字符出现的次数
    s = Counter(s)                                      # 计算可迭代序列中元素的数量，返回字典类型数据
    chs, freqs = s.keys(), s.values()
    nums = count()                                      # 创建一个从start=0开始的无限迭代器，每次迭代加上step=1
    # 构造堆
    tree = list(zip(freqs, nums, chs))                  # 创建列表，列表中每项为一个三元组（fregs：出现频率，nums：序号,chs：字符名)
    heapify(tree)                                       # 基于tree列表，构建堆
    # 合并结点，构造哈夫曼树
    while len(tree)>1:
        fa, _, a = heappop(tree)                        # 从堆中弹出并返回最小的元素，保持堆属性
        fb, _, b = heappop(tree)
        heappush(tree, (fa + fb, next(nums), [a,b]))    # 将一个元素压入堆中，保持堆属性
    print('='*30)
    print(tree)
    print('='*30)
      
    return tree[0][2]                                   # tree为列表，tree[0][0]堆顶元素和，tree[0][1]：结点序号，tree[0][2]：字符化的树结构
                                                        # tree = [(36, 20, [[['r', 'e'], [['d', 'f'], ['j', 'w']]], ['a', [[['s', 'g'], 'c'], 'b']]])]
    
def get_table(tree, prefix=''):                         # tree：待编码子树，prefix：编码前已确定的树前哈夫曼编码
    # 遍历哈夫曼树，为每个字符编码
    if isinstance(tree, str):
        yield (tree, prefix)                            # yield：返回生成器
        return
    for bit, child in zip('01', tree):
        for pair in get_table(child, prefix+bit):
            yield pair
            
def main(s):
    print(s)
    tree = huffman_tree(s)
    print('='*50)
    gener_test = get_table(tree)
    for item in gener_test:
        print(item)
    print('='*50)
    table = dict(get_table(tree))                       # 单个get_table返回的的是一个生成器。每个生成器的内容为（'字符名称','字符对应的哈夫曼编码')
    print(table)
    # 根据哈夫曼编码表对字符串进行编码
    code = ''.join(map(lambda ch: table[ch],s))         # s字符串的更换为哈夫曼编码后，以空格分割
    print(code)
    # 根据哈夫曼编码表进行解码
    code = '0101101101001'                              # 此处可以输入待解码的哈夫曼编码
    ss = ''
    while len(code) > 0:
        for ch, c in table.items():
            if code.startswith(c):
                ss = ss + ch
                code = code[len(c):]                    # code右移，移出已匹配的编码
    print()
    print(ss)
    
main('baaabbcbbbcdcdfsraejajgfweraawaearaa')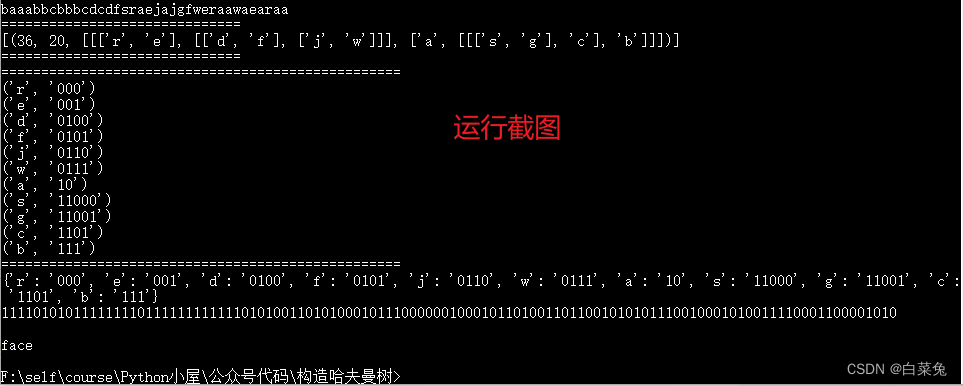

引用位置（不带注释）：Python实现哈夫曼编码与解码