吴恩达《机器学习》——线性回归代码实现

线性回归

- 1. 单变量线性回归
- - 单变量线性回归公式
  - 损失函数
  - 优化算法——批梯度下降（BGD）
- 2. 多变量线性回归
- - 特征缩放（标准化）
  - 参数的逆缩放
- 3. 线性回归算法代码实现
- - 向量实现
  - Python代码
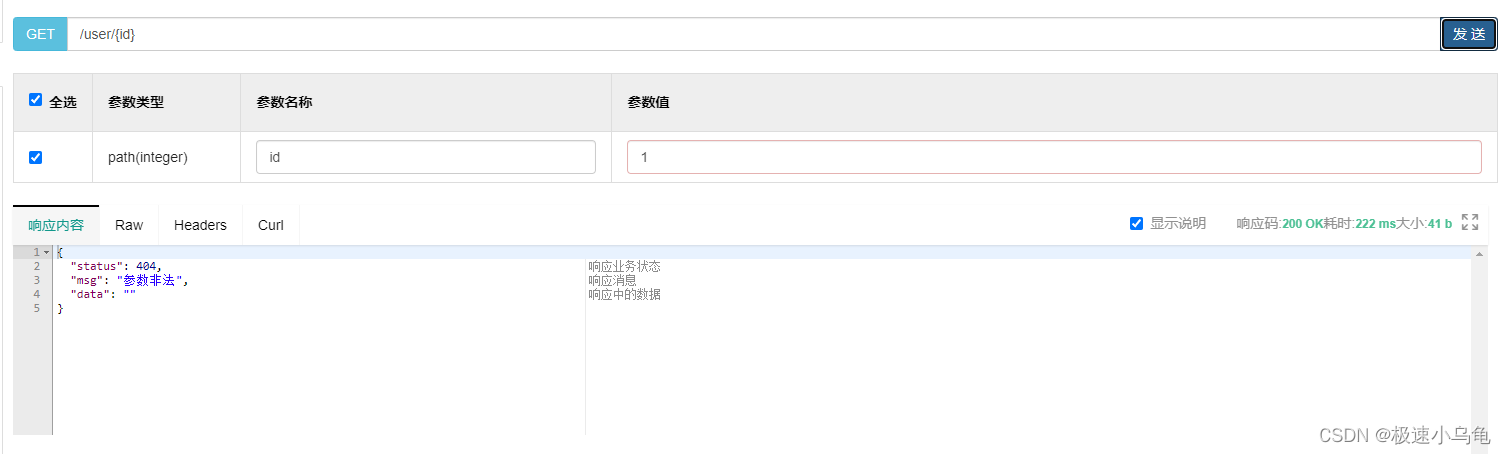
- 4. 实验结果
- - 单变量回归
  - 多变量回归
  - 实验总结

数据集、源文件可以在Github项目中获得

地址：https://github.com/Raymond-Yang-2001/AndrewNg-Machine-Learing-Homework

1. 单变量线性回归

单变量线性回归找到一维方程，拟合一条直线。

单变量线性回归公式

$h_{w,b}(x)=b+wx$
$w$ 和 $b$ 是参数，为了方便运算，可以给 $x$ 加上一个 $x_0=1$
$h_{w,b}(x)=bx_{0}+wx_{1}$

损失函数

$J(w,b)=\frac{1}{2m}\sum_{i=1}^{m}(h_{w,b}(x^{(i)})-y^{(i)})^{2}$
为了避免不恰当的数据范围带来损失过大或过小，（例如若数据数值过大，损失可能会在 $10^5$ 或者 $10^6$ 这个数量级，不适合直观分析）在评估损失的时候，可以对 $h_{w,b}(x^{(i)})$ 和 $y^{(i)}$ 先进行标准化，使得损失数值在可评估的范围内。但在进行梯度下降时，不进行此操作

优化算法——批梯度下降（BGD）

$w_j=w_{j}-\alpha\frac{\partial}{\partial{w_j}}{J(w,b)}=w_{j}-\alpha \frac{1}{m}\sum_{i=1}^{m}{(h_{w,b}(x^{(i)})-y^{(i)})x^{(i)}}$
$b_j=b_{j}-\alpha\frac{\partial}{\partial{b_j}}{J(w,b)}=w_{j}-\alpha \frac{1}{m}\sum_{i=1}^{m}{(h_{w,b}(x^{(i)})-y^{(i)})}$
这里，我们可以使用 $\theta$ 统一标识参数，包括 $w$ 和 $b$ 。

即，第 $j$ 个参数 $\theta_j$ 的更新可以写为：
$\theta_{j}=\theta_{j}-\alpha\frac{\partial}{\partial{w_j}}{J(\theta;\mathbf{x})}=w_{j}-\alpha \frac{1}{m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}}$
其中 $\alpha$ 是学习率。

2. 多变量线性回归

多变量线性回归试图找出多个变量和预测值之间的关系。例如，房子大小、房子卧室数量和房价之间的关系。

特征缩放（标准化）

在样本的不同特征数值差异过大的时候，基于梯度的优化方法会出现一些问题。例如存在如下回归方程：
$h_{\theta}(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}$
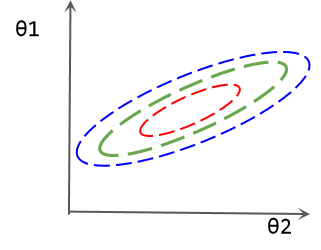
假设 $x_{2}$ 的范围是 $0\sim1$ ， $x_1$ 的范围是 $10^3\sim10^4$ 。我们根据梯度同时优化 $\theta_0\sim\theta_2$ ，使得其均改变了相同的大小，那么显然在输入样本相同的情况下， $\theta_1$ 的变动会比 $\theta_2$ 导致更大的输出的变化。这也可以理解为模型对 $\theta_1$ 更敏感。如下损失等线图所示， $\theta_1$ 的微小变动会带来损失的剧烈变化。这种情况下，参数的优化会更加困难。
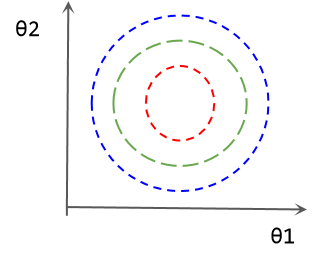
在这里插入图片描述
解决这个问题的方法之一就是特征缩放，将两个特征缩放到相同的范围内。例如，可以进行z-score标准化工作：
$x_{new} = \frac{x-\mu}{\sigma}$
其中， $\mu$ 是数据集的均值， $\sigma$ 是标准差，新数据的分布是均值为0，标准差为1的分布。
数据标准化后的参数等损失图如下所示：
在这里插入图片描述

参数的逆缩放

由于对数据进行了缩放，所以最后得到的参数也会出现相应的缩放。其具体关系如下：
$\theta_{0}+\theta_{1\sim d+1}\frac{x_{1\sim d+1}-\mu_{x}}{\sigma_{x}}=\frac{y-\mu_{y}}{\sigma_{y}}$
这里我们对 $y$ 也进行了标准化，事实上也可以不这么做，对性能没有任何影响。但是对y的标准化使得参数变得更小，对于初始化为0的参数能更快达到收敛。

在标准化 $y$ 这种情况下，参数的逆缩放公式为：
$\theta_{1\sim d+1}^{new}=\frac{\theta_{1\sim d+1}}{\sigma_{x}}\sigma_{y}$
得到：
$\theta_{0}\sigma_{y}+\theta_{1\sim d+1}^{new}(x_{1\sim d+1}-\mu_{x})=y-\mu_{y}$

$\theta_{0}^{new}=\theta_{0}\sigma_{y}+\mu_{y}-\theta_{1\sim d+1}^{new}\mu_{x}$
其中，在向量化运算时， $\theta_{1\sim d+1}^{new}$ 和 $\mu_{x}$ 均为(1,d)的向量，乘法应该采用向量内积。

3. 线性回归算法代码实现

向量实现

设数据 $\boldsymbol{x}$ 的维度是 $(n, d)$ ，其中n是样本数量，d是样本特征的维度。为了计算方便，我们在样本上添加一个额外数值全为1的特征维度，使其维度变为 $(n, d + 1)$

预测
令参数 $\boldsymbol{\theta}$ 的维度为(1, d+1)，则 $\boldsymbol{x\theta^{\top}}$ 或 $\boldsymbol{(\theta x^{\top})^{\top}}$ 可以得到维度为 $(n, 1)$ 的预测结果 $h_{\boldsymbol{\theta}}(\boldsymbol{x})$ 。
梯度下降
第j个参数的梯度下降公式为：
$\theta_{j}=\theta_{j}-\alpha\frac{\partial}{\partial{w_j}}{J(\theta;\mathbf{x})}=w_{j}-\alpha \frac{1}{m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}}$
事实上，这里我们把 $\theta_{0}$ 作为偏置，其梯度应该为：
$\frac{\partial}{\partial{w_0}}{J(\theta;\mathbf{x})}=w_{0}-\alpha \frac{1}{m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})}$ ，由于我们在数据中补充了全为1的特征维度 $x_0$ ，所以其可以和其他参数一样使用上面的公式计算。
设 $error$ 矩阵 $\boldsymbol{\beta}$ 为 $h_{\boldsymbol{\theta}}(\boldsymbol{x})-\boldsymbol{x}$ ，维度为 $(n, 1)$ ，则 $\boldsymbol{x^{\top}\beta} /n$ 是维度为 $(d + 1, 1)$ 的梯度矩阵。
$\boldsymbol{x^{\top}\beta}= \left[ \begin{matrix} x^{(1)}& x^{(2)} &\cdots \end{matrix} \right] \times \left[ \begin{matrix} h(x^{(1)})-y^{(1)}\\ h(x^{(2)})-y^{(2)}\\ \vdots \end{matrix} \right] =\left[ \begin{matrix} \sum_{i=1}^{n}{(h(x^{(i)})-y^{(i)})x_{0}^{(1)}}\\ \sum_{i=1}^{n}{(h(x^{(i)})-y^{(i)})x_{1}^{(1)}}\\ \vdots \end{matrix} \right]$
$\boldsymbol{x^{\top}\beta} /n$ 中的每个元素就是对应参数的梯度。

Python代码

import numpy as np


def square_loss(pred, target):
    """
    计算平方误差
    :param pred: 预测
    :param target: ground truth
    :return: 损失序列
    """
    return np.sum(np.power((pred - target), 2))


def compute_loss(pred, target):
    """
    计算归一化平均损失
    :param pred: 预测
    :param target: ground truth
    :return: 损失
    """
    pred = (pred - pred.mean(axis=0)) / pred.std(axis=0)
    target = (pred - target.mean(axis=0)) / target.std(axis=0)
    loss = square_loss(pred, target)
    return np.sum(loss) / (2 * pred.shape[0])


class LinearRegression:
    """
    线性回归类
    """

    def __init__(self, x, y, val_x, val_y, epoch=100, lr=0.1):
        """
        初始化
        :param x: 样本, (sample_number, dimension)
        :param y: 标签, (sample_numer, 1)
        :param epoch: 训练迭代次数
        :param lr: 学习率
        """
        self.theta = None
        self.loss = []
        self.val_loss = []
        self.n = x.shape[0]
        self.d = x.shape[1]

        self.epoch = epoch
        self.lr = lr

        t = np.ones(shape=(self.n, 1))

        self.x_std = x.std(axis=0)
        self.x_mean = x.mean(axis=0)
        self.y_mean = y.mean(axis=0)
        self.y_std = y.std(axis=0)

        x_norm = (x - self.x_mean) / self.x_std
        y_norm = (y - self.y_mean) / self.y_std

        self.y = y_norm
        self.x = np.concatenate((t, x_norm), axis=1)

        self.val_x = val_x
        self.val_y = val_y

    def init_theta(self):
        """
        初始化参数
        :return: theta (1, d+1)
        """
        self.theta = np.zeros(shape=(1, self.d + 1))

    def validation(self, x, y):
        x = (x - x.mean(axis=0)) / x.std(axis=0)
        y = (y - y.mean(axis=0)) / y.std(axis=0)
        outputs = self.predict(x)
        curr_loss = square_loss(outputs, y) / (2 * y.shape[0])
        return curr_loss

    def gradient_decent(self, pred):
        """
        实现梯度下降求解
        """
        # error (n,1)
        error = pred - self.y
        # gradient (d+1, 1)
        gradient = np.matmul(self.x.T, error)
        # gradient (1,d+1)
        gradient = gradient.T / pred.shape[0]
        # update parameters
        self.theta = self.theta - (self.lr / self.n) * gradient

    def train(self):
        """
        训练线性回归
        :return: 参数矩阵theta (1,d+1); 损失序列 loss
        """
        self.init_theta()

        for i in range(self.epoch):
            # pred (1,n); theta (1,d+1); self.x.T (d+1, n)
            pred = np.matmul(self.theta, self.x.T)
            # pred (n,1)
            pred = pred.T
            curr_loss = square_loss(pred, self.y) / (2 * self.n)
            val_loss = self.validation(self.val_x, self.val_y)
            self.gradient_decent(pred)
            
            self.val_loss.append(val_loss)
            self.loss.append(curr_loss)
            print("Epoch: {}/{}\tTrain Loss: {:.4f}\tVal loss: {:.4f}".format(i + 1, self.epoch, curr_loss, val_loss))

        # un_scaling parameters
        self.theta[0, 1:] = self.theta[0, 1:] / self.x_std.T * self.y_std[0]
        self.theta[0, 0] = self.theta[0, 0] * self.y_std[0] + self.y_mean[0] - np.dot(self.theta[0, 1:], self.x_mean)
        return self.theta, self.loss, self.val_loss

    def predict(self, x):
        """
        回归预测
        :param x: 输入样本 (n,d)
        :return: 预测结果 (n,1)
        """
        # (d,1)
        t = np.ones(shape=(x.shape[0], 1))
        x = np.concatenate((t, x), axis=1)
        pred = np.matmul(self.theta, x.T)
        return pred.T

4. 实验结果

单变量回归

数据集可视化
在这里插入图片描述
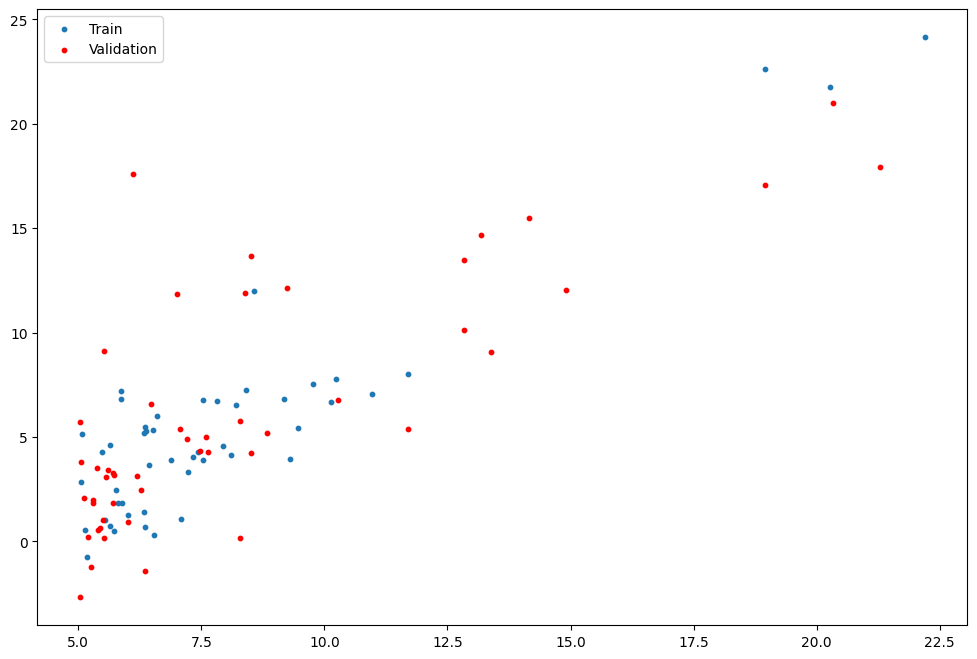
训练集与测试集划分
blog.csdnimg.cn/c92b41d0e88f4afab794315c992525a0.png)

from LinearRegression import LinearRegression

epochs = 200
alpha = 1
linear_reg = LinearRegression(x=train_x_ex,y=train_y_ex,val_x=val_x_ex, val_y=val_y_ex, lr=alpha,epoch=epochs)
start_time = time.time()
theta,loss, val_loss = linear_reg.train()
end_time = time.time()

Train Time: 0.0309s
Val Loss: 6.7951

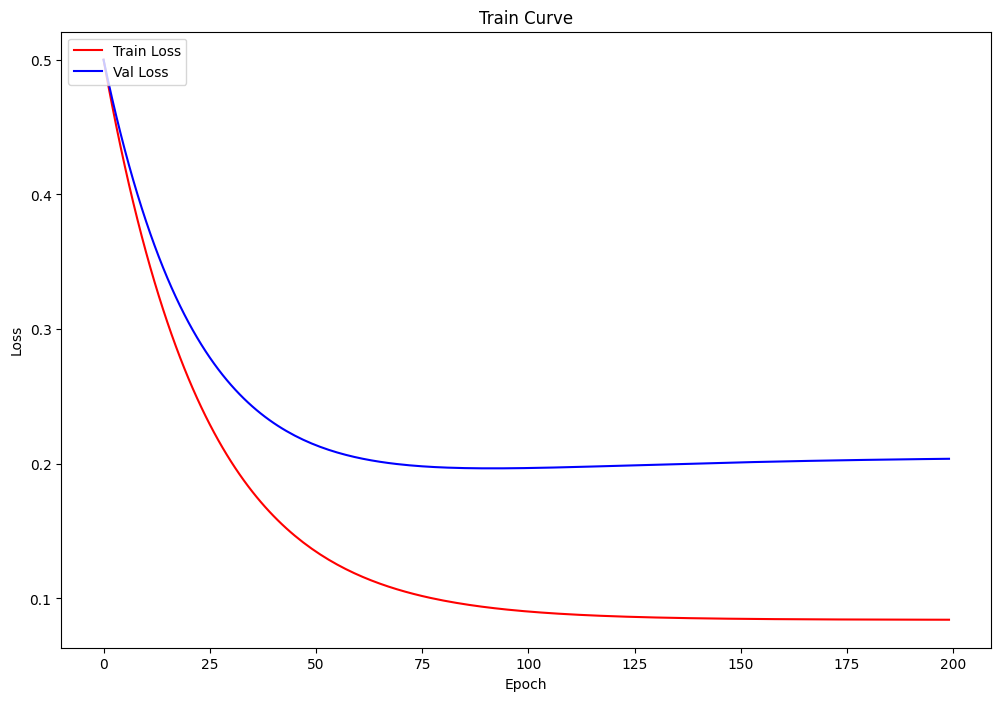
训练过程可视化
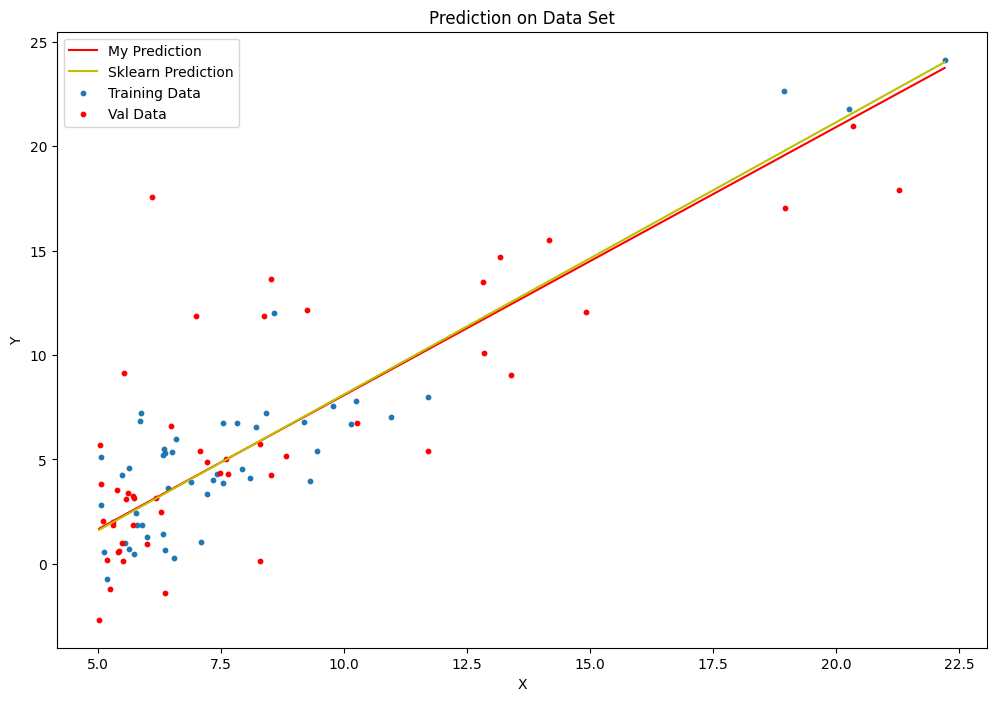
在这里插入图片描述
与sk-learn比较预测曲线

多变量回归

数据可视化与训练集、验证集
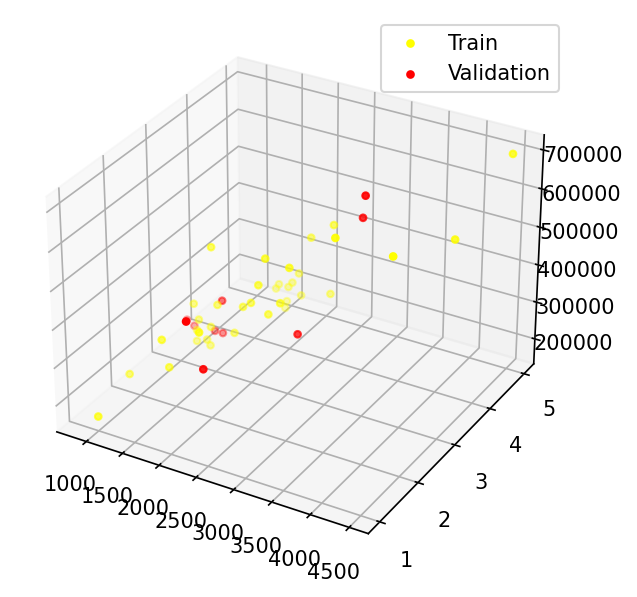
在这里插入图片描述

from LinearRegression import LinearRegression

alpha = 0.1
epochs = 1000
multi_lr = LinearRegression(train_x,train_y_ex,val_x=val_x,val_y=val_y_ex, epoch=epochs,lr=alpha)
start_time = time.time()
theta, loss, val_loss = multi_lr.train()
end_time = time.time()

Train Time: 0.1209s
Val Loss: 4.187（采用归一化后数据计算损失）

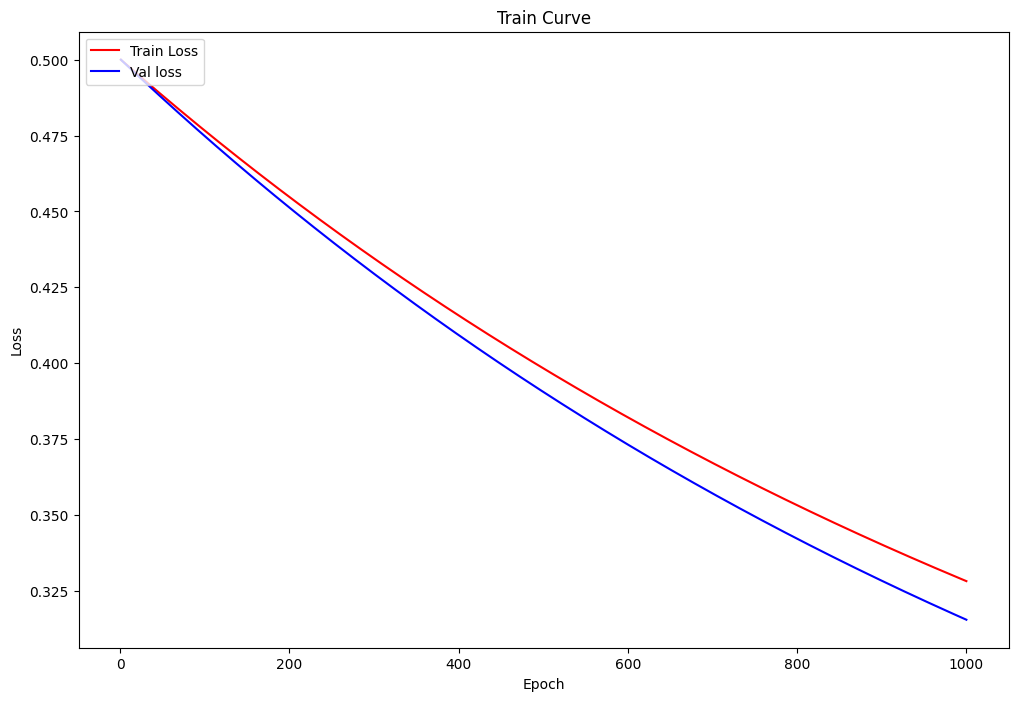
训练过程可视化
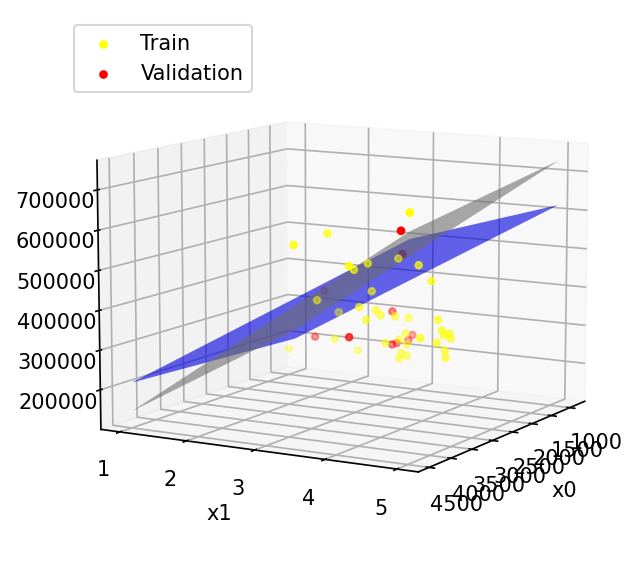
在这里插入图片描述

预测平面（与sk-learn对比）
其中蓝色为本算法的预测平面，灰色为sk-learn的预测平面
在这里插入图片描述

实验总结

对于线性回归算法的实现打到了较好的性能，可以尝试调节学习率或者迭代次数来获得更好的性能。由于采用了矩阵运算代替了循环，所以训练时间大大缩短，但仍未到达sk-learn库函数的水平。