之前的文章 信号去噪 中列出了7种常用的信号去噪算法，对于后两种算法——深度学习和奇异值分解(SVD)，我现在也不太理解，就先不写了。

很多朋友留言又提了一些算法，今天一起来聊聊椭圆滤波器。

椭圆滤波器（Elliptic Filter），也称为Cauer滤波器，是一种数字滤波器，用于信号处理和滤波应用。椭圆滤波器之所以得名，是因为其在频率响应图上的特征呈现出椭圆形的形状。

椭圆滤波器有以下特点和优点：

1. 极窄的过渡带宽：椭圆滤波器的过渡带宽（即通频带到阻频带的过渡区域）非常窄，这意味着它可以在频域内实现非常陡峭的滤波特性。

2. 通带和阻带均衡：椭圆滤波器通常可以在通带和阻带内实现更好的幅度响应均衡。这意味着它可以在通带内最小化幅度失真，并在阻带内最大化信号抑制。

3. 允许通带和阻带的波动：与其他滤波器设计相比，椭圆滤波器允许通带和阻带内的振荡，但在给定的通带和阻带容限下，可以实现更小的阶数（更低的复杂度）。

4. 高阶滤波特性：椭圆滤波器通常以较高的阶数实现，这使其适用于需要极高滤波性能的应用，如无线通信和雷达系统。

椭圆滤波器的设计需要确定以下参数：

• 通带边界频率（通带上下限的频率）。
• 阻带边界频率（阻带上下限的频率）。
• 通带最大允许波纹（通带内振荡的幅度波纹）。
• 阻带最小抑制（阻带内信号抑制的最小要求）。

椭圆滤波器设计通常涉及到数学优化问题，以找到最佳参数配置来满足上述要求。

椭圆滤波器的设计

滤波器的目标

任何滤波器的目标都是根据特定的频率响应特性来修改输入信号的频谱。在椭圆滤波器中，通常有以下几个重要的频率响应特性目标：

• 通带（Passband）：这是允许信号通过的频率范围，通常是我们希望保留的信号频率范围。
• 阻带（Stopband）：这是我们希望完全抑制的频率范围，通常包括噪声或干扰信号。
• 过渡带（Transition Band）：这是从通带到阻带之间的频率范围，通常需要在此范围内实现平滑的过渡。

频率响应特性

椭圆滤波器的主要特点是它在通带和阻带内具有波纹，这意味着幅度响应在这些频率范围内会波动。设计椭圆滤波器时，需要指定以下几个关键参数：

• 通带上限和下限频率。
• 阻带上限和下限频率。
• 通带内的最大允许波纹（通带内振荡的幅度波纹）。
• 阻带内的最小抑制要求（阻带内信号抑制的最小要求）。

设计优化

设计椭圆滤波器通常是一个优化问题，其中的目标是找到一组滤波器系数，以满足上述频率响应特性和参数要求。这个问题通常涉及到复杂的数学和优化算法。

阶数

椭圆滤波器的性能和复杂度与其阶数有关。阶数是滤波器的系数数量，通常以n表示。增加阶数可以提高滤波器的性能，但也会增加计算复杂度。

通带和阻带特性

椭圆滤波器的主要特点是通带和阻带内的波纹，这些波纹是通过合适的设计参数来控制的。通带波纹是通带内的最大振荡幅度，而阻带波纹是阻带内允许的最小信号抑制。

通带和阻带边界

设计椭圆滤波器时，需要指定通带和阻带的频率边界。这些边界决定了滤波器在哪些频率范围内工作以及哪些频率范围内抑制信号。

滤波器的实现

一旦设计出椭圆滤波器的系数，它可以被实现为数字滤波器。在数字信号处理中，可以使用差分方程或频域方法来应用这些系数。

性能权衡

椭圆滤波器的设计涉及性能和复杂度之间的权衡。增加阶数和降低通带和阻带波纹可以提高性能，但会增加计算复杂度。设计者需要根据具体应用的需求来选择合适的权衡。

应用

椭圆滤波器在各种领域都有广泛的应用，包括通信、图像处理、生物医学工程和音频处理等。下面是椭圆滤波器在音频处理中的应用实例之一——音频均衡器。

应用实例：音频均衡器

音频均衡器是音频处理中常见的设备，用于调整不同频率范围内的音频信号的增益，以满足特定的声音质量和音频效果要求。通常，音频均衡器分为多个频带，每个频带可以独立地调整增益，以实现音频的均衡。

在音频均衡器中，椭圆滤波器用于实现不同频带的均衡。每个频带都有一个椭圆滤波器，它可以调整该频带内的音频信号的增益，同时保持其他频带不受影响。以下是一个音频均衡器的应用示例：

信号描述： 假设我们有一个音频均衡器，它分为低音、中音和高音三个频带。我们希望用户能够通过调整这三个频带的增益来实现音频的均衡，即增强或减弱不同频率范围内的声音。

解决方案： 对于每个频带，我们可以使用椭圆滤波器来实现频率范围内的增益控制。椭圆滤波器的通带可以定位在相应频带内，而阻带则可以防止信号泄漏到其他频带。用户可以通过旋钮或界面上的控制来调整每个频带的增益。

性能： 椭圆滤波器可以设计为非常陡峭的滤波器，具有出色的频率选择和抑制特性。这使得它们非常适合用于音频均衡器，因为它们可以准确地控制每个频带的音频信号，而不会对其他频带产生不希望的影响。

实际应用： 音频均衡器广泛用于音响系统、录音室设备、电视和广播设备等领域。用户可以根据音频播放环境和个人喜好来调整音频的均衡，以获得更好的音质和听觉体验。

这个示例说明了椭圆滤波器在音频均衡器中的应用，帮助实现不同频带的音频均衡和定制。这对于音频处理和音响应用中的声音调整非常重要。

python示例

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import ellip, lfilter
from scipy.fft import fft

# 生成一个示例音频信号
fs = 44100  # 采样率
t = np.arange(0, 0.1, 1/fs)  # 时间向量
frequencies = [100, 500, 1000, 5000]  # 音频信号的频率成分
signal = np.sum([np.sin(2 * np.pi * f * t) for f in frequencies], axis=0)

# 设计椭圆滤波器
# 假设我们有3个频带，每个频带的通带和阻带频率范围由用户定义
band1 = (50, 200)  # 低音频带
band2 = (400, 800)  # 中音频带
band3 = (800, 5000)  # 高音频带

# 设计低音频带的椭圆滤波器
low_band = ellip(4, 0.05, 40, [2 * f / fs for f in band1], 'bandpass', analog=False)

# 设计中音频带的椭圆滤波器
mid_band = ellip(4, 0.5, 40, [2 * f / fs for f in band2], 'bandpass', analog=False)

# 设计高音频带的椭圆滤波器
high_band = ellip(4, 0.5, 40, [2 * f / fs for f in band3], 'bandpass', analog=False)

# 使用滤波器处理信号
filtered_signal1 = lfilter(*low_band, signal)
filtered_signal2 = lfilter(*mid_band, signal)
filtered_signal3 = lfilter(*high_band, signal)

# 计算频谱
def calculate_spectrum(x, fs):
    N = len(x)
    spectrum = np.abs(fft(x))[:N // 2]
    frequency = np.fft.fftfreq(N, 1 / fs)[:N // 2]
    return frequency, spectrum

# 计算原始信号的频谱
freq_original, spec_original = calculate_spectrum(signal, fs)

# 计算处理后的信号频谱
freq_filtered1, spec_filtered1 = calculate_spectrum(filtered_signal1, fs)
freq_filtered2, spec_filtered2 = calculate_spectrum(filtered_signal2, fs)
freq_filtered3, spec_filtered3 = calculate_spectrum(filtered_signal3, fs)

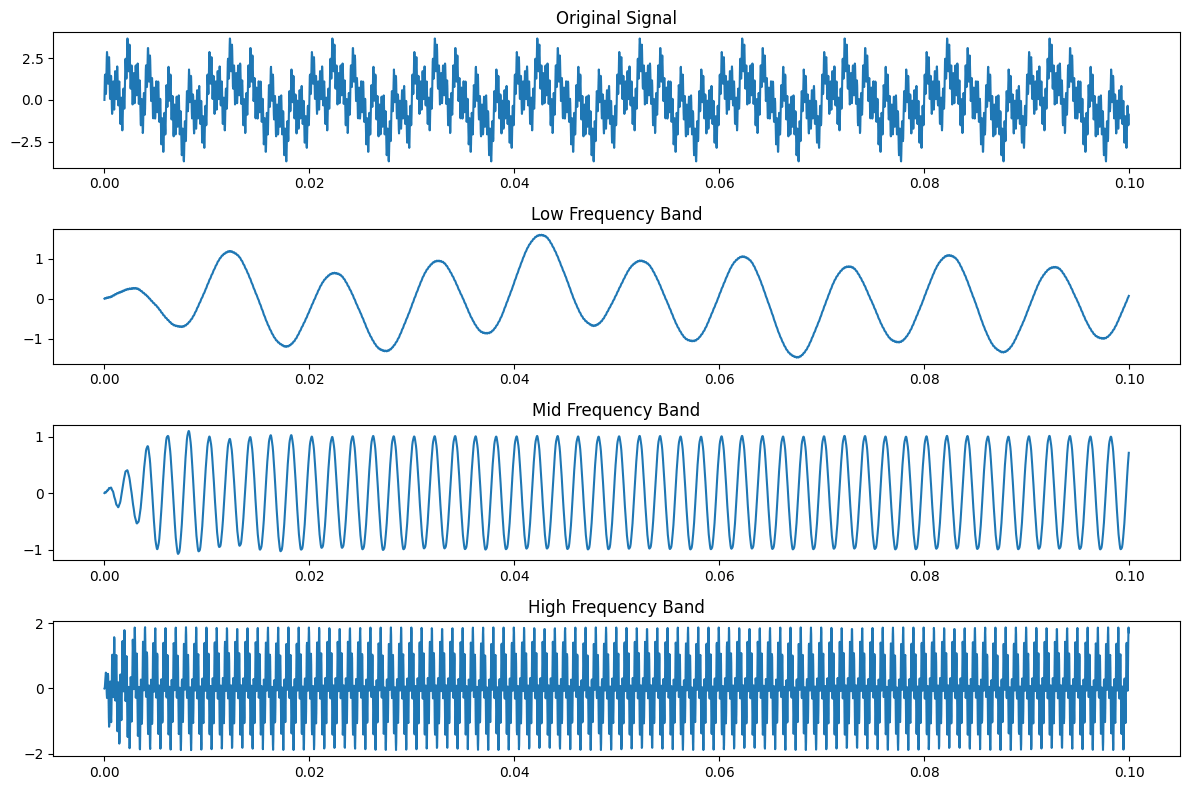
# 绘制原始信号和处理后的信号
plt.figure(figsize=(12, 8))

plt.subplot(4, 1, 1)
plt.title('Original Signal')
plt.plot(t, signal)

plt.subplot(4, 1, 2)
plt.title('Low Frequency Band')
plt.plot(t, filtered_signal1)

plt.subplot(4, 1, 3)
plt.title('Mid Frequency Band')
plt.plot(t, filtered_signal2)

plt.subplot(4, 1, 4)
plt.title('High Frequency Band')
plt.plot(t, filtered_signal3)

plt.tight_layout()

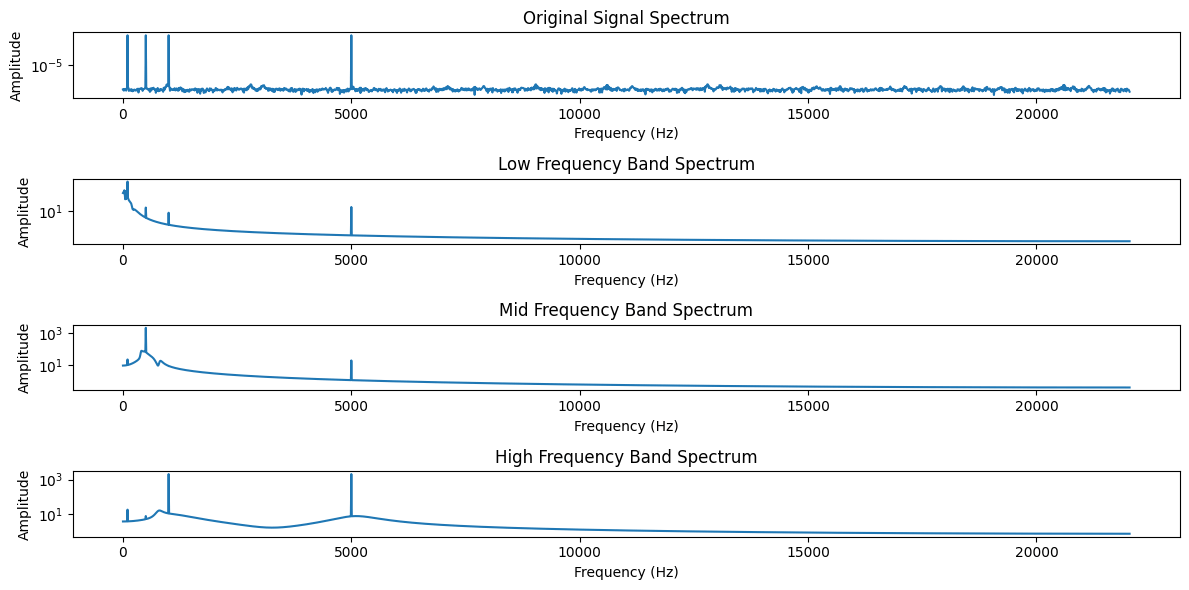
# 绘制频谱图
plt.figure(figsize=(12, 6))

plt.subplot(4, 1, 1)
plt.title('Original Signal Spectrum')
plt.semilogy(freq_original, spec_original)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')

plt.subplot(4, 1, 2)
plt.title('Low Frequency Band Spectrum')
plt.semilogy(freq_filtered1, spec_filtered1)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')

plt.subplot(4, 1, 3)
plt.title('Mid Frequency Band Spectrum')
plt.semilogy(freq_filtered2, spec_filtered2)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')

plt.subplot(4, 1, 4)
plt.title('High Frequency Band Spectrum')
plt.semilogy(freq_filtered3, spec_filtered3)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')

plt.tight_layout()
plt.show()

输出：

公众号 | FunIO
微信搜一搜 “funio”，发现更多精彩内容。
个人博客 | blog.boringhex.top