目录
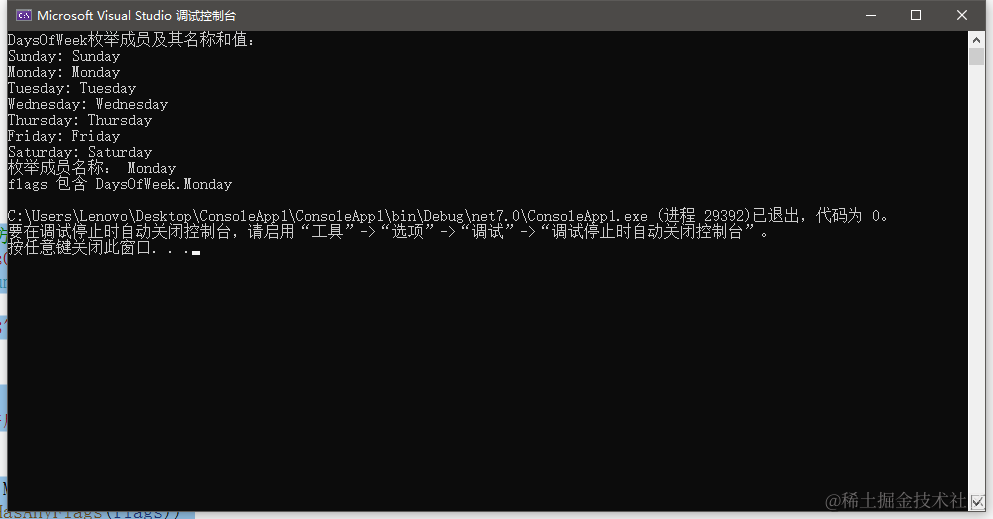
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
5.算法完整程序工程
1.算法运行效果图预览
2.算法运行软件版本
MATLAB2022a
3.部分核心程序
................................................................
%调制识别
len1 = func_fsk_psk_check(p1);
len2 = func_fsk_psk_check(p2);
len3 = func_fsk_psk_check(p3);
len4 = func_fsk_psk_check(p4);
%根据参数获得FSK和PSK区分参数
Level= (mean([len1,len2]) - mean([len3,len4]))/2;
%分别提取FSK和PSK的不同调制方式的特征参数
char1 = real(func_para_check(y_2FSKn,N0));
char2 = real(func_para_check(y_4FSKn,N0));
char3 = real(func_para_check(y_2PSKn,N0));
char4 = real(func_para_check(y_4PSKn,N0));
%通过GRNN神经网络进行训练
char = [char1;char2]';
T = [1;2]';
net_fsk = newgrnn(char,T,1.2);
char = [char3;char4]';
T = [1;2]';
net_psk = newgrnn(char,T,1.2);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%加载信号进行测试
%通过大量的循环测试,计算正确率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
zql = 0;
%运行的时候,尽量将下面的两个参数指标设置大点,这样结果才精确
MTKL = 50;
SNRS = [-10:1:20];
Bers = zeros(length(SNRS),1);
for jj = 1:length(SNRS)
for i = 1:MTKL
[SNRS(jj),i]
rng(i);
%长度
N = N0;
%SNR
SNR = SNRS(jj);
%2FSK
y_2FSK = func_2FSK(N);
%4FSK
y_4FSK = func_4FSK(N);
%BPSK
y_2PSK = func_2PSK(N);
%QPSK
y_4PSK = func_4PSK(N);
%设置单独的一种调制信号
tmps = [2,2,2,2];%4PSK
if tmps(1) == 1
datas = y_2FSK;
end
if tmps(1) == 2
datas = y_4FSK;
end
if tmps(1) == 3
datas = y_2PSK;
end
if tmps(1) == 4
datas = y_4PSK;
end
datas = func_multipath(datas);
data = func_add_noise(datas,SNR);
[p,f] = func_power(data,Ns);
len = func_fsk_psk_check(p);
flag = 0;
%首先进行FSK和PSK两种模式的区分
if len >= Level%为FSK模式
%根据识别参数进行调制类型的辨识
char = real(func_para_check(data,length(data)));
T = round(sim(net_fsk,char'));
if T == 1
flag = 1;
end
if T == 2
flag = 2;
end
else%为PSK模式
%根据识别参数进行调制类型的辨识
char = real(func_para_check(data,length(data)));
T = round(sim(net_psk,char'));
if T == 1
flag = 3;
end
if T == 2
flag = 4;
end
end
if flag == tmps(1)
zql = zql + 1;
end
end
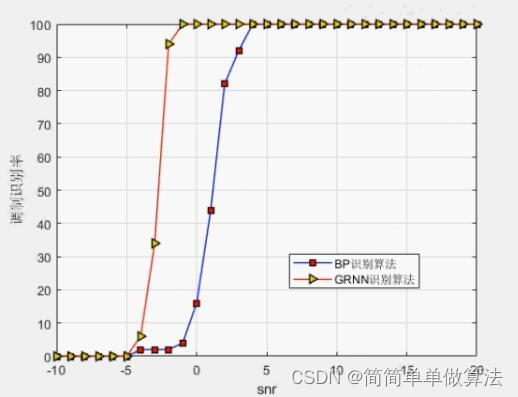
%识别正确率
Bers(jj) = zql/MTKL;
zql = 0;
end
R = 100*mean(Bers,2);
figure;
plot(SNRS,R,'b-o','linewidth',2);
grid on
xlabel('snr');
ylabel('调制识别率');
axis([min(SNRS)-1,max(SNRS)+1,0,110]);
save r1.mat SNRS R
01_131m4.算法理论概述
本课题,我们主要对MPSK和MFSK调制类型进行识别。在进行信号调制方式区分之前,首先需要对PSK和FSK进行区分,提出了一种基于信号功率谱的PSK和FSK调制方式的识别方法。信号的功率谱计算过程,是一个计算随机过程的统计特性的过程,其中平稳随机过程的功率谱计算过程是一个确定的函数,计算信号的功率谱的过程即功率谱估计。是通过给定的信号样本去估计平稳随机信号的功率谱密度,通过计算信号的功率谱估计可以分析信号的能量随着频率分布的变化情况。
信号的功率谱计算方法可以分为经典谱估计方法和现代谱估计方法目前应用较为广泛的是经典谱估计算法。经典谱估计方法主要分为直接法和间接法两大类别,本文将通过直接法对调制信号的功率谱进行估计,直接法的主要流程是先计算调制信号的快速傅里叶变换,将调制信号从时域变换到频域,然后将频域结果与其共轭结果相乘,从而得到信号的功率谱估计。
该算法的整体流程图如下所示

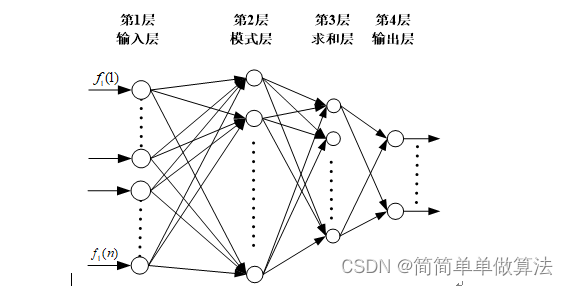
GRNN,即General Regression Neural Network,中文全称为广义回归神经网络,是由The Lockheed Palo Alto研究实验室在1991年提出的。GRNN是一种新型的基于非线性回归理论的神经网络模型[43,44]。GRNN是建立在非参数核回归基础之上的,该神经网络是以测试样本为后验条件,并从观测样本中计算得到自变量和因变量之间的概率密度函数,然后在计算出因变量关于自变量的回归值。由于GRNN不需要规定模型的类型,只需要设置神经网络的光滑因子参数,GRNN神经网络的光滑因子参数的取值对神经网络的输出影响较大,当光滑因子参数较大的时候,其对应的神经元所覆盖的输入区域就越大;当光滑因子参数较小的时候,神经网络对应的径向基函数曲线较陡,因此神经网络输出结果更接近期望值,但此时光滑度越差。
GRNN结构如图所示,整个网络包括输入层、模式层、求和层与输出层。
5.算法完整程序工程
OOOOO
OOO
O