拓扑排序（Java实现）

news2024/11/28 0:29:51

一、基本思想

拓扑排序是一种对有向无环图（DAG）进行排序的算法，它将所有顶点排成一个线性序列，使得对于任意一条有向边（u, v），u在序列中都出现在v之前。拓扑排序的思想非常直观，就像是按照任务的先后顺序制定一个任务列表，每个任务都依赖于前面的任务完成后才能开始。

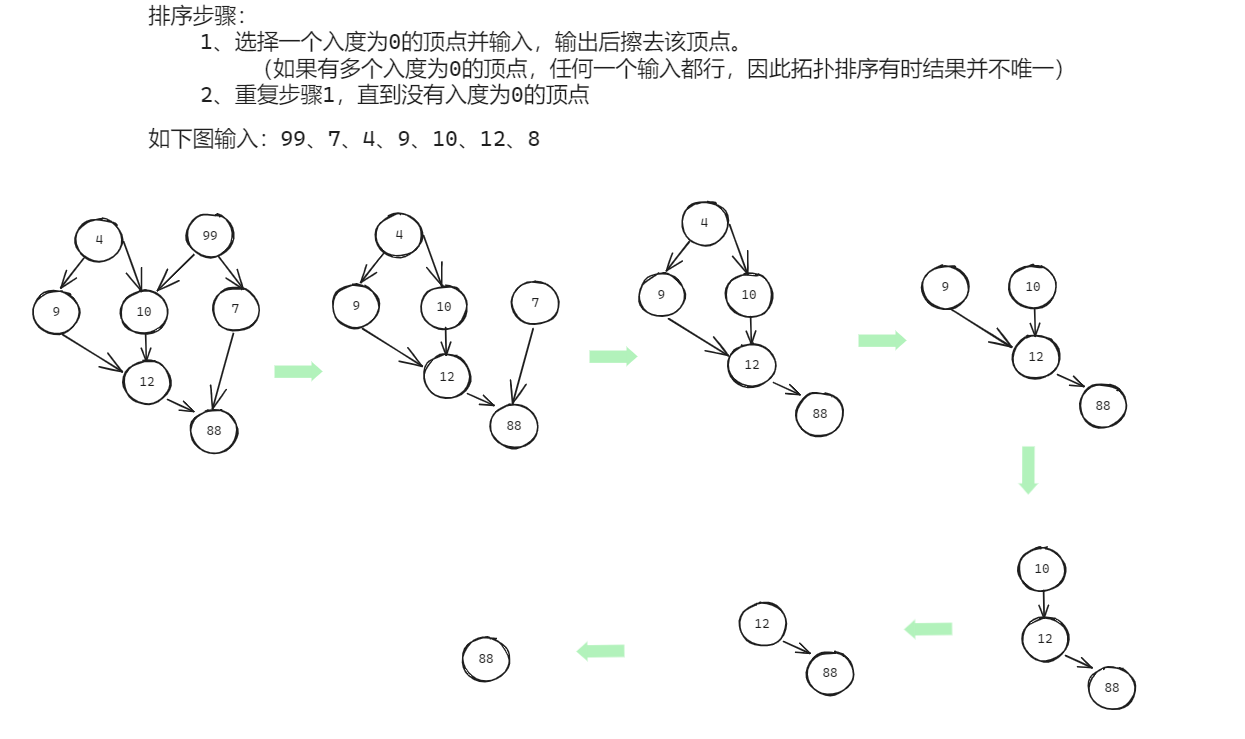
拓扑排序的算法实现主要包括两个步骤：

构造有向图：首先需要按照一定的顺序构造有向图，记录每个节点的入度(节点A指向B则称A为B的入度）。这一步可以通过遍历整个图来实现。
进行拓扑排序：从图中选择一个入度为0的顶点，输出该顶点，并从图中删除该顶点和所有以它为起点的有向边。重复这一步骤直到所有顶点均已输出，或者当前图中不存在入度为0的顶点为止。如果此时图中仍存在入度为0的顶点，则说明有向图中必然存在环，因此不可能进行拓扑排序。

拓扑排序的结果不唯一，只要满足任意一对顶点之间的先后关系即可。因此，在实际应用中，可以根据具体问题的要求选择不同的拓扑排序算法。

拓扑排序的应用范围非常广泛，在Java中拓扑排序通常用于具有依赖关系的任务调度，例如在确定任务执行的顺序、制定课程表、解决比赛日程安排等问题中都可以应用。通过拓扑排序，我们可以将复杂的问题分解为小问题，并按照一定的顺序进行解决，从而提高解决问题的效率。

什么是有向无环图？

有向无环图（Directed Acyclic Graph，DAG）是一种特殊的图，它由顶点（Vertex）和边（Edge）组成。每条边都有一个方向，从一条边的起点到终点。在有向图中，如果存在一条路径可以回到起点，那么这个图就是一个环。而有向无环图的定义就是不存在这样的环。换句话说，有向无环图是一种有向图，它无法从某个顶点出发经过若干条边回到该点。

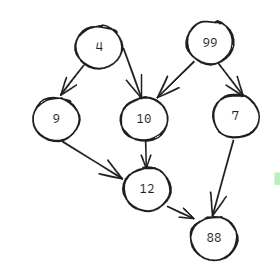
如下图就是一个有向无环图

对上面这个图进行拓扑排序？

二、Java实现案例

案例：课程学习顺序

描述：现在你总共有 numCourses 门课需要选（课程序号从0开始，即表示0到numCourses - 1的课）。给你一个数组 prerequisites ，其中 prerequisites[i] = [a, b] ，表示在选修课程 a 前必须先选修 b。返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回任意一种就可以了。如果不可能完成所有课程，返回一个空数组。

代码实现：

public int[] findOrder(int numCourses, int[][] prerequisites) {
    if (numCourses <= 0) return new int[0];
    // 1. 构造有向图。（邻接表）存放每个节点的后继节点
    HashSet<Integer>[] adjacency = new HashSet[numCourses];
    for (int i = 0; i < numCourses; i++) {
        adjacency[i] = new HashSet<>();
    }
    // 2. 记录每个节点的入度值
    int[] inDegree = new int[numCourses];
    for (int[] p : prerequisites) {
        adjacency[p[1]].add(p[0]);
        inDegree[p[0]]++;
    }
    // 3. 将入度为0的课程加入队列
    Queue<Integer> queue = new LinkedList<>();
    for (int i = 0; i < numCourses; i++) {
        if (inDegree[i] == 0) queue.offer(i);
    }
    // 4. 拓扑排序，每次将入度为0的课程取出来放入结果集中，并将该课程的后继节点入度值-1
    int[] result = new int[numCourses];
    int index = 0; //记录当前已安排的课程数
    while (!queue.isEmpty()) {
        int course = queue.poll();
        result[index++] = course;
        for (Integer adjacentCourse : adjacency[course]) {
            inDegree[adjacentCourse]--;
            if (inDegree[adjacentCourse] == 0) {
                queue.offer(adjacentCourse);
            }
        }
    }
    // 5. 如果结果列表中的课程数不等于总课程数，说明无法完成所有课程，返回空数组
    if (index != numCourses) return new int[0];

    return result;
}