贝叶斯网络简介
贝叶斯网络(Bayesian network)也叫贝氏网路、信念网络(belief network)或是有向无环图(DAG)模型,是一种概率图模型。它利用DAG的结构,得到一组随机变量{X1,X2,...,Xn}的条件概率分布(conditional probability distributions, or CPDs)。它的作用简单来说就是:通过分析因果关系来理解数据。
一般而言,DAG中节点表示随机变量,包括可观测变量,或潜在变量、未知参数。连接两个节点的箭头代表这两个随机变量是具有因果关系或非条件独立的;若没有箭头连接二者的情况就称随机变量彼此间条件独立。单箭头的起点是“因”,终点是“果”;两节点之间产生一个条件概率值。
贝叶斯网络的应用包括:疾病和相关症状间的概率关系(已知症状,计算各疾病的发生概率);生物信息学中基因调控网络、蛋白质结构分析、基因表达分析等;各个领域的决策支持系统;电力故障分析,如利用因果分析技术帮助电力、能源等公司找到电力系统中的风险所在等。
贝叶斯网络是一种强有力的基于概率的不确定性推理方法。它可以模拟某个变量改变会产生什么样的结果,比如天气的改变会如何影响能源供给和购物的状况。贝叶斯网络和神经网络的最大区别和优势是,前者的运作过程有透明性,不是黑盒子。
贝叶斯网络的计算方法
贝叶斯网络的计算方法分为精确推导法和随机推导法。前者包括列举推理法、变量消除推理法(variable elimination)。后者包括直接取样推导法、拒绝取样推导法、概率加权推导法、马尔可夫链蒙特卡罗推导法。本文介绍精确推导法中的两个方法。
列举推理法
假如有两个服务器S1和S2,会发送数据包到用户端(用U表示)。而S2的发送成功率与S1的成功与否有关。其DAG结构图表示如下。对每个数据包传输,只有两个可能值:T(成功)或 F(失败)。那么就有如下的联合概率公式:
现在思考一个问题:假设用户U已经收到数据包,那么S1发送数据成功的概率是多大?
即我们要求!
而已知{S1}的真值表、{S1,S2}的真值表、{S1,S2,U}的真值表,这个问题是可以直接手动推导的!
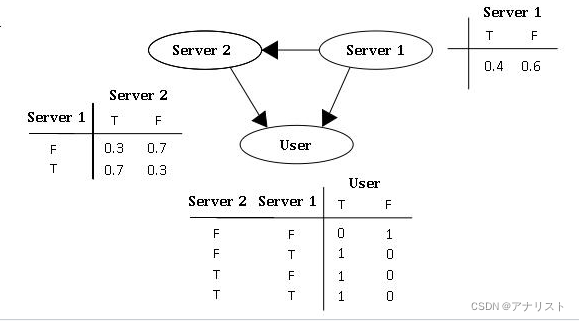
推导如下:

变量消除推理法
在BN(贝叶斯网络)中,我们把叫做边际概率(Marginal Probability),把
叫做条件概率,其中E可以是单个或联合证据(conjunctive evidence)。这里的X叫做查询变量(query variable),E叫做证据变量(evidence variable),所有其他变量都叫隐变量(hidden variable)。注意:边际概率的意思是,我们没有得到任何证据。我们通常对后验概率感兴趣,也就是某件事已经发生,想计算这件事发生的原因是由某个因素引起的概率。
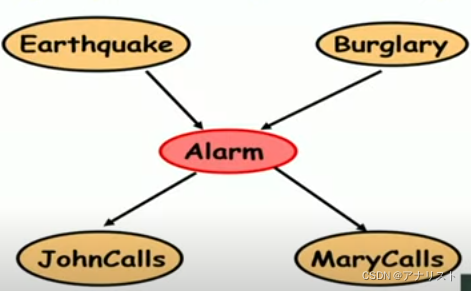
现在考虑一个案例,名字叫“如果John和Mary都打电话(Call)给你,那么发生入室盗窃(Burglary)的概率是多少?”。
故事的背景如下:假如你正在参加一个聚会,突然John打电话给你,你离开聚会并接听,他说家里有警报(Alarm),但是他说的话不一定是事实(只是具有某个概率),因为他经常喝醉。然后没多久Mary也打电话给你,说回家吧,家里有警报(Alarm),同样她的话可信度也对应一个概率。现在你需要弄清楚这是由入室盗窃(Burglary)引起的警报,还是由地震(Earthquake)引起的警报,或者他俩都说的谎话(喝醉产生幻觉或故意开玩笑)。
你要求的是
第一步:,其中j,m都是小写,分别表示J,M的具体值,这里是J=True, M=True
(注:大写字母表示随机变量,需要处理它的所有可能值。因此P(B| j, m)就表示当John和Mary都打电话来时,家里发生入室盗窃(Burglary)的概率是多大,未发生的概率是多大)
第二步:显然上式分母是个常数,不重要。当J为真,M为真,分母对于入室盗窃的真假,是个恒定的值。而分子P(B,j, m)将随B的取值(True或False)变化而变化。
因此我们可以简单说:P(B| j, m)与P(B,j, m)成正比。比例性的另一个说法是,乘以某个alpha,于是我们有
第三步:注意这个例子一共有5个变量,在完全联合分布中有2^5=32个可能的组合。现在目标公式考虑了BJM三个变量,就有2^2=4个情况可以表示:(地震为真,警报为真)、(地震为真,警报为假)、(地震为假,警报为真)、(地震为假,警报为假)。我们可以写为对隐变量求和的完整联合分布。于是得到:
第四步:根据该问题的贝叶斯网络的DAG结构,我们进一步得到
重点:贝叶斯网络的完整联合分布始终可以通过拓扑顺序乘以所有条件概率来表示。
第五步:进一步做代数整理,把拆解成
和
的分步求和,也就是所谓的逐步变量消除。为此,先对A求和,再对E求和,就得到:
第六步:为进一步理解上述公式,我们画一个计算图。考虑B为真(True)的场景,即要计算这个概率值,根据公式应该是
假设入室盗窃发生的概率(即P(b))为0.001,地震发生的概率(即P(e))为0.002,那么地震未发生的概率(即P(¬e))为0.998;假设入室盗窃和地震都发生时,警报响的概率(即P(a|b,e))为0.95,那么此时警报不响的概率(即P(¬a|b,e))为0.05;假设入室盗窃发生而地震未发生时,警报响的概率(即P(a|b,¬e))为0.94,那么此时警报不响的概率(即P(¬a|b,¬e))为0.06;假设警报响而John打来电话的概率(即P(j|a))为0.90;假设警报响而Mary打来电话的概率(即P(m|a))为0.70;假设警报不响而John打来电话的概率(即P(j|¬a))为0.05;假设警报不响而Mary打来电话的概率(即P(m|¬a))为0.01。那么,就得到如下的贝叶斯网络概率图,其中含“+”的圈圈表示求和节点(即∑),而不含“+”的圈圈表示乘法节点。
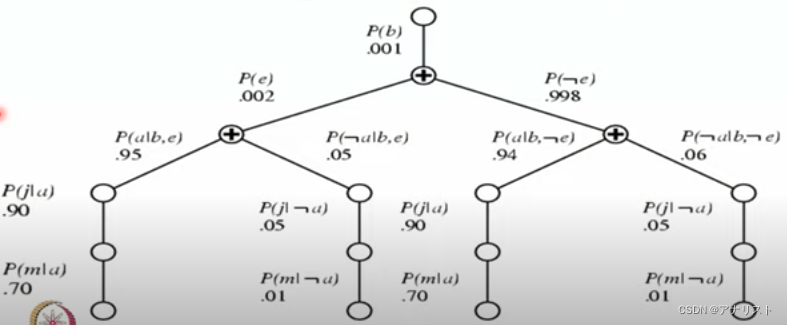
需要指出,上图底部两侧计算是重复的、冗余的,可用动态规划(DP)计算。本文不作过多讨论。
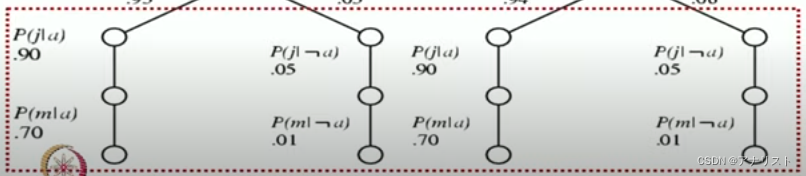
重点:在贝叶斯网络中进行计算推理的动态编程算法,就叫做变量消除(Variable Elimination)。
变量消除(VE)使用名称因子(factor),因子是一个函数,VE通过按顺序消除所有变量,直到因子只剩下查询变量(Query Variable )。为了消除一个变量,必须联合包含该变量的所有因子;输出该变量对新的因子的影响之和;输出乘积形式的联合分布(Joint distribution)。
变量消除(VE)的例子
还是上面的例子,现在我们求P(J)
上式中消去了E变量,是A和B的函数!
因此,原式可改写为
上式中消去了B变量,是A的函数!
因此,原式可改写为
上式中消去了M变量,是A的函数!
因此,原式可改写为
上式又消去了A变量,是J的函数!
因此,原式可改写为
以上展示了变量消除(VE)推理法是如何工作的。它线性化创建这些计算的序列,并且不断返回。
变量消除(VE)的特定数值计算
我们回到第五步的公式
其中是A的函数,我们分别列出
和
的真值表,如下

表中数据和DAG中一致。
现在计算的真值表,如下

我们可以把上式命名为f1,它的取值为0.63和0.005,即

我们的公式变成了
接下来对给定(E,B)的A条件概率乘以A的f1求和,即考虑
由于是一个必要的假设前提,我们直接给出真值表,如下:

解释如下:地震发生、盗窃发生,警报响的概率是0.95,警报不响的概率是0.05;地震发生、盗窃未发生,警报响的概率是0.29,警报不响的概率是0.71;地震未发生、盗窃发生,警报响的概率是0.94,警报不响的概率是0.06;地震未发生、盗窃未发生,警报响的概率是0.001,警报不响的概率是0.999。
注意是对A求和,消去A变量,因此是E、B的函数,得到:

我们把上式叫做,就有:

我们的公式变成了,显然E被求和、消去,所以它是B的函数!(当然,B只有True和False两个可能值)
现在考虑除去的部分,即
又已知B和E的真值表,如下

表中数据和DAG中一致。
我们得到的真值表如下

我们不妨把叫做
,计算后就有
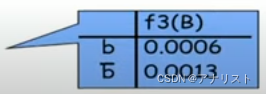
而我们的原公式变成了
现在思考如何把与概率分布
更好对应起来,即
![]()
可以发现真值表的总和不为1,我们要对它进行归一化。

归一化常数为0.0019,每个概率值要除以它。我们得到:

这就是我们最终要求的概率。
意思是,如果John和Mary都打电话(Call)给你,那么发生入室盗窃(Burglary)的概率是0.32!
这就是使用变量消除在贝叶斯网络中进行推理的方法。
变量消除(VE)推理法的总结
一. 每个操作只是各个因子的简单乘法,并进行累加
二. 复杂度取决于最大的因子,比如在本文的例子中是3个变量,而不是5个(因为j,m都已知);复杂度正比于变量数;和最大因子的消除顺序成指数相关;最优消除顺序的求解是N-hard问题;可以用启发式的方法求解,以及用特殊数据结构(如polytree)
三. 没有魔法
polytree的相关资料:
https://en.wikipedia.org/wiki/Polytree







![[BUUCTF NewStar 2023] week5 Crypto/pwn](https://img-blog.csdnimg.cn/b72e3abe449d476b85135804cb1a0304.png)