快速傅里叶变换FFT其实是一种对离散傅里叶变换DFT的快速算法
为了便于公式推导和理解，本文从DFT的公式出发进行解释，在帕萨瓦尔定律的条件下，探究如何保证FFT/IFFT前后信号功率保持一致。

---

模型假设

我们假设有一长度为1024的序列$x(n)$，作N=1024点的FFT后得到$X(K)$
$$X(k)=DFT[x(n)]=\sum _{n=0}^{N-1}x(n)e^{-j\frac{2\pi }{N}nk}(0\le k\le N-1)$$
$$x(n)=IDFT[X(k)]=\frac{1}{N}\sum _{k=0}^{N-1}X(k)e^{j\frac{2\pi }{N}kn}(0\le n\le N-1)$$
可以简单记作$x(n)\leftrightarrow X(k)$
根据有限长序列的帕萨瓦尔定律（具体推导可见该博客）
$$\sum _{n=0}^{N-1}|x(n){|}^2=\frac{1}{N}\sum _{k=0}^{N-1}|X(k){|}^2$$
可以得知，对于有限长序列，在一个频域带限内，频域上的功率谱之和与时域上信号的功率有一个N倍的关系。

简单来说，FFT之后的信号的功率比原始信号的功率大了N倍。

FFT前后功率保持一致

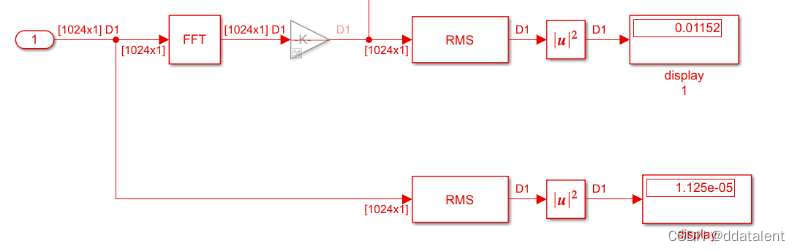
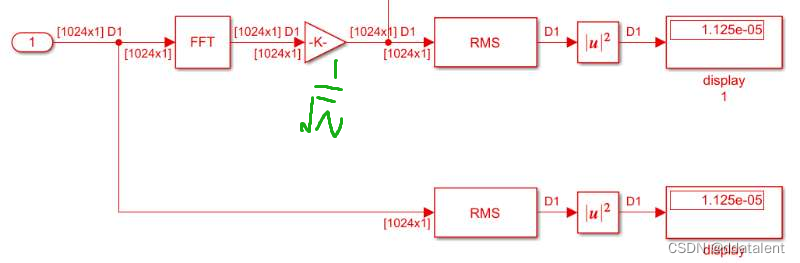
仿真结果如上图所示，0.01152/0.00001125=1024，FFT后的信号功率大了1024倍。为了使得FFT前后信号功率保持一致，需要对FFT后的数据乘以系数$\frac{1}{\sqrt{N}}$。对一个复数乘以$\frac{1}{\sqrt{N}}$的增益，则其功率变为原来的$\frac{1}{N}$，保证了FFT前后信号功率一致。

IFFT前后功率保持一致

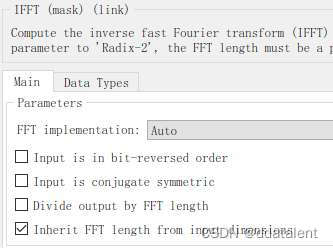
simulink的IFFT模块中，默认是不勾选“除以N”这个选项的。
也就是说IFFT的公式
$$x(n)=IDFT[X(k)]=\frac{1}{N}\sum _{k=0}^{N-1}X(k)e^{j\frac{2\pi }{N}kn}(0\le n\le N-1)$$
在simulink中默认是
$$IDFT[X(k)]=\sum _{k=0}^{N-1}X(k)e^{j\frac{2\pi }{N}kn}(0\le n\le N-1)$$

我们是习惯于不改变模块默认值的，以便模型具有通用性。因此，我们通常在IFFT模块后面添加一个$\frac{1}{N}$的增益模块

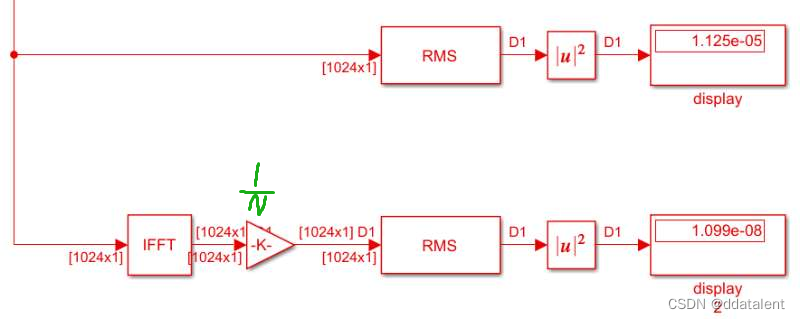
这样我们就得到了标准的$x(n)\leftrightarrow X(k)$。
而之前我们说过，对于标准的离散傅里叶变换对，其频域功率是时域功率的N倍。因此我们需要在标准的IFFT之后，对于时域信号再添加一个$\sqrt{N}$的增益模块。
$\frac{1}{N}$的增益模块和$\sqrt{N}$的增益模块可以合并为$\frac{1}{\sqrt{N}}$的增益模块。因此，我们在默认的IFFT模块后面也只需要添加一个$\frac{1}{\sqrt{N}}$的增益模块即可使得IFFT前后的信号功率保持一致。

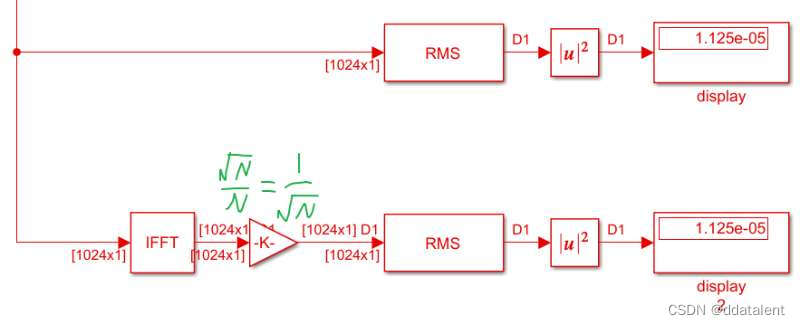
总结

不论是IFFT还是FFT，都需要在默认的IFFT/FFT模块后面添加一个$\frac{1}{\sqrt{N}}$的增益模块，即可使得时域信号和频域信号的功率保持一致。