---

优先级队列（堆）的概念+模拟堆的实现

---

一、概念

1.优先级队列

优先级队列 Priority Queue

• 队列中操作的数据带有优先级，出队的时候，优先级高的先出
• 可以返回最高优先级对象，可以添加新的对象
• 在Java1.8中，priorityQueue的底层使用了堆，堆的相当于对完全二叉树进行了调整

2.堆

• 将一个关键码的集合中所以元素，按照完全二叉树的顺序，存进一个一维数组当中

1.堆的性质

1.堆中结点的值，总是不大于/不小于它父亲结点的值

2.堆总是一棵完全二叉树

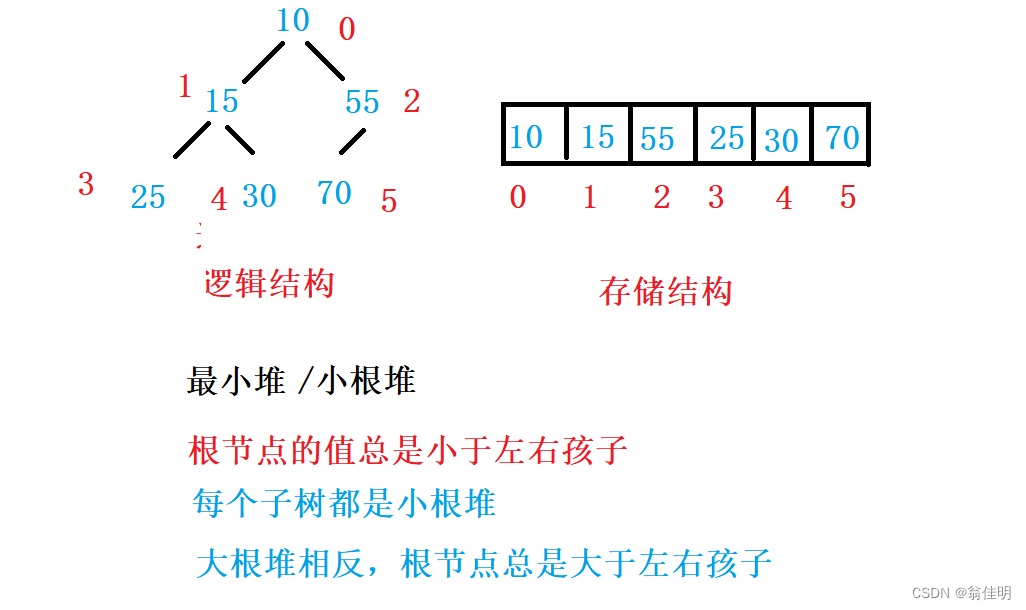
2.堆的存储

• 堆是一棵完全二叉树，层序的规则可以用顺序的方法来存储

• 完全二叉树从上到下，从左往右依次排列，存进数组中没有空的位置

• 结点在数组下标为i,其双亲结点为（ i - 1 ）/ 2

• 左孩子：2 * i +1 ; 右孩子：2 * i + 2

3.堆的创建

3.1 向下调整

每棵树都向下调整，维护大根堆

• 向下调整的时间复杂度：== 树的高度

• 向下调整建堆的时间复杂度：O(n)

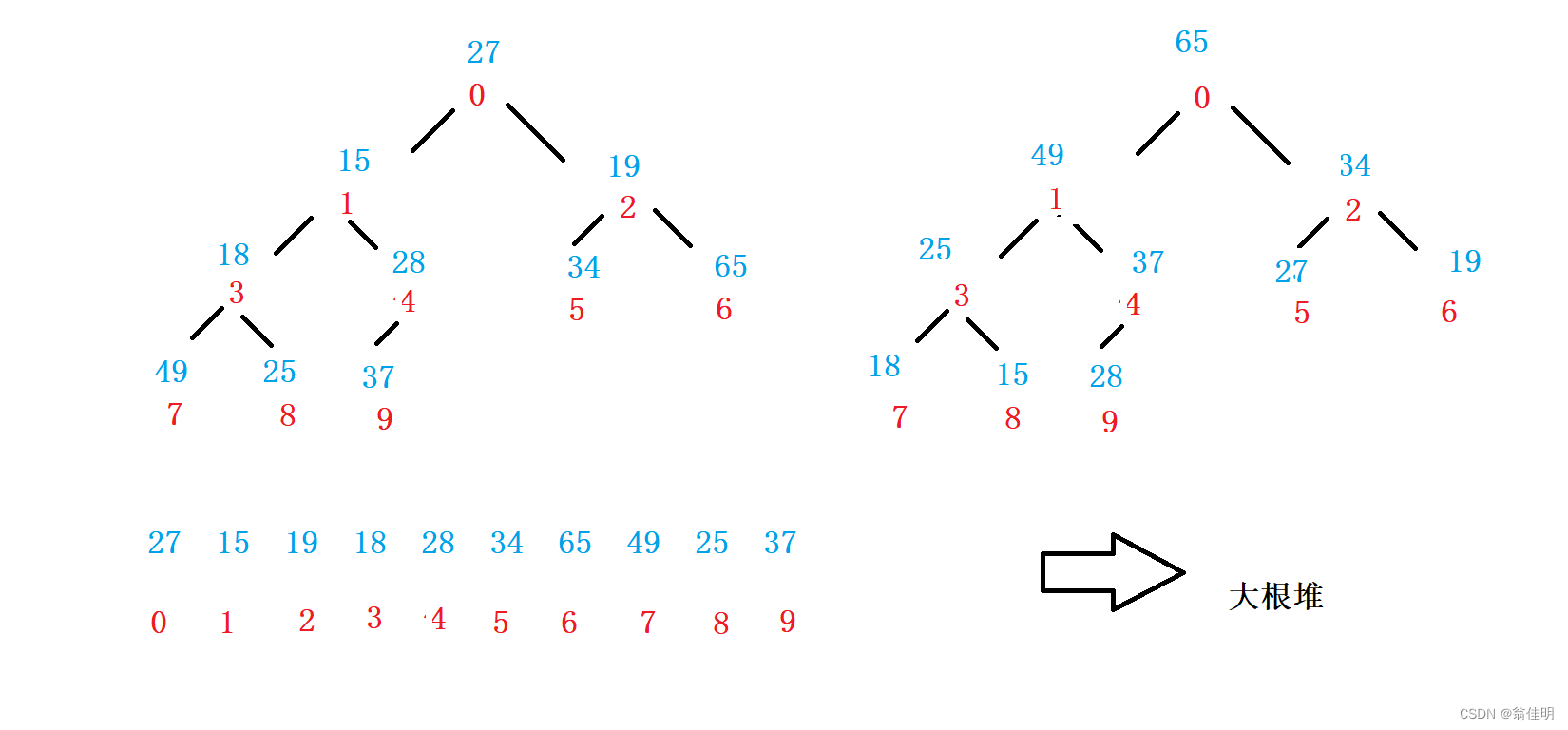
• 每棵树从父结点向下走，要找到每棵树的父结点

• 从最后一棵子树来进行调整，找到最后一个结点和它的双亲结点，遍历得到父结点的下标

• 找到最大的子节点，比较后进行交换

public class TestHeap {
    public int[] elem;//底层是一个一维数组
    public int usedSize;//记录当前堆中有多少条数据

    public TestHeap() {
        this.elem = new int[10];
    }

    public void initElem(int[] array) {//初始化
        for (int i = 0; i < array.length; i++) {
            elem[i] = array[i];
            usedSize++;
        }
    }
}

1.进行初始化

    public void createHeap() {//堆的创建
        //最后一个结点的下标= usedSize-1,它的双亲结点的下标= (usedSize-1-1)/2
        for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {//求出parent
            shiftDown(parent, usedSize);//结束下标传usedSize
            //结束的结点下标的值不会超过usedSize
        }
    }

    /**
     * 父亲下标
     * 每棵树的结束下标
     *
     * @param parent
     * @param len
     */
    private void shiftDown(int parent, int len) {//向下调整，每棵树从父结点向下走
        int child = 2 * parent + 1;
        // child < len最起码要有一个左孩子
        while (child < len) {
            //child + 1保证一定有右孩子的情况下，和右孩子比较
            if (child + 1 < len && elem[child] < elem[child + 1]) {//右孩子大
                child++;
            }
            //保证child的下标是左右孩子最大值的下标
            if (elem[child] > elem[parent]) {//如果子节点的值比父结点的大，交换
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;

                parent = child;//交换完成后，让parent结点等于等于当前child结点,
                child = 2 * parent + 1;//重新求子节点的位置，再次进入循环交换

            } else {
                break;//比父结点小，结束循环
            }
        }
    }

堆的创建

1.遍历得到每个双亲结点，根据双亲结点找到子节点，保证child的下标是左右孩子最大值的下标

2.子节点和父结点比较并交换

3.2建堆的时间复杂度 O(N)

向下调整的方式建立大根堆、小根堆，时间复杂度约等于O(n)

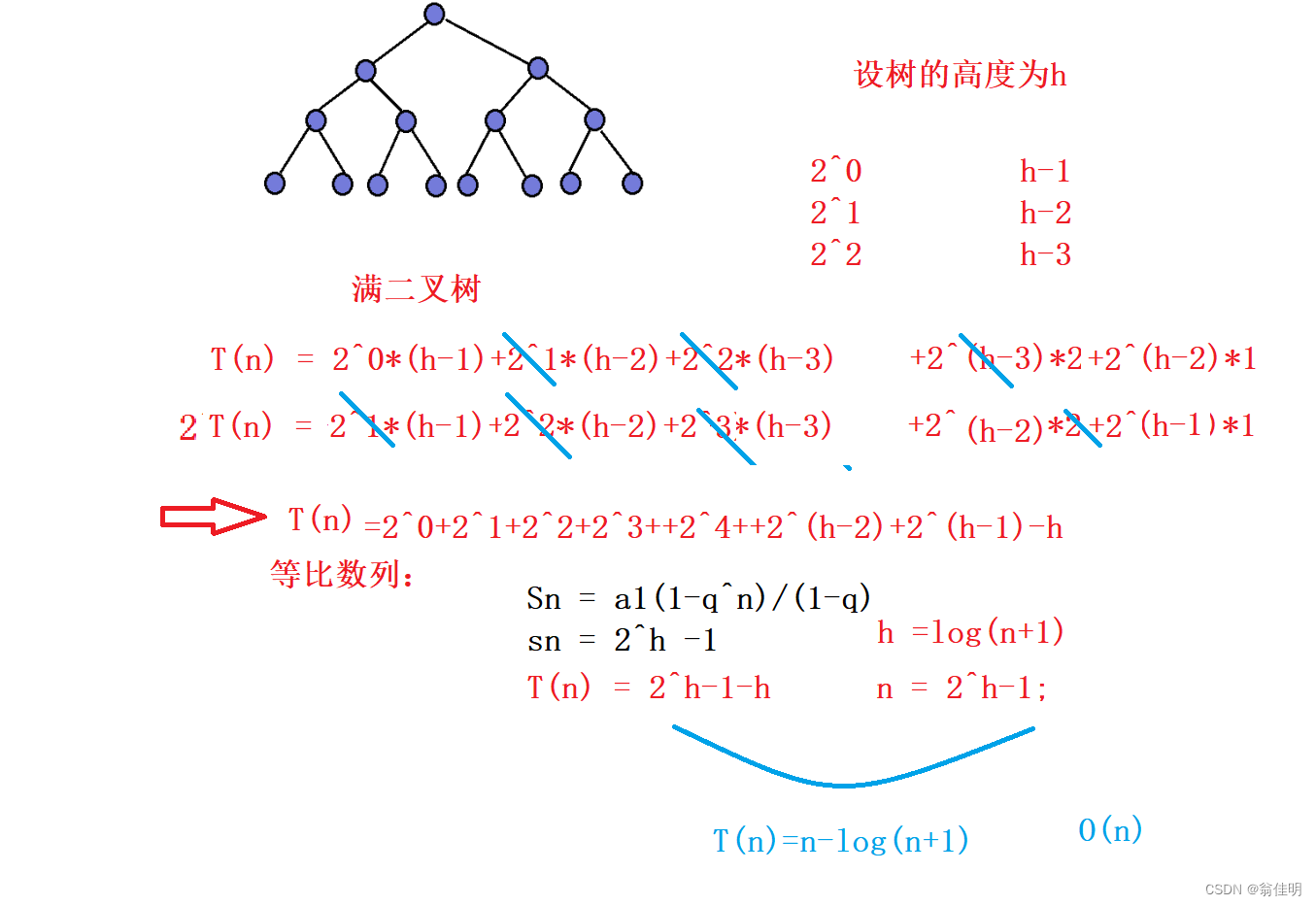
用满二叉树来分析

4.堆的插入

    public void offer(int val) {
        if (isFull()) {//如果满了就扩容
            elem = Arrays.copyOf(elem, 2 * elem.length);
        }
        elem[usedSize++] = val;//存到最后
        //进行向上调整
        shiftUp(usedSize - 1);//传进孩子结点的下标

    }

    public boolean isFull() {
        return usedSize == elem.length;
    }

    private void shiftUp(int child) {//向上调整，已知孩子结点的下标求父亲结点的下标
        int parent = (child - 1) / 2;
        while (child > 0) {//循环结束的条件就是child =0
            if (elem[child] > elem[parent]) {//比较、交换
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                child = parent;
                parent = (child - 1) / 2;
            } else {
                break;
            }
        }
    }

4.1向上调整

• 插入到有效数据的最后,空间不够要扩容，成为新的子节点，已知孩子结点，求父亲结点
• 向上调整，调整的过程中，直接和父结点比较，如果比父结点的值大就交换
• 不用比较左右孩子的最大值，因为根节点的子树本身就是大根堆，不用进行维护

4.2向上调整建堆的时间复杂度：O(N * log N)

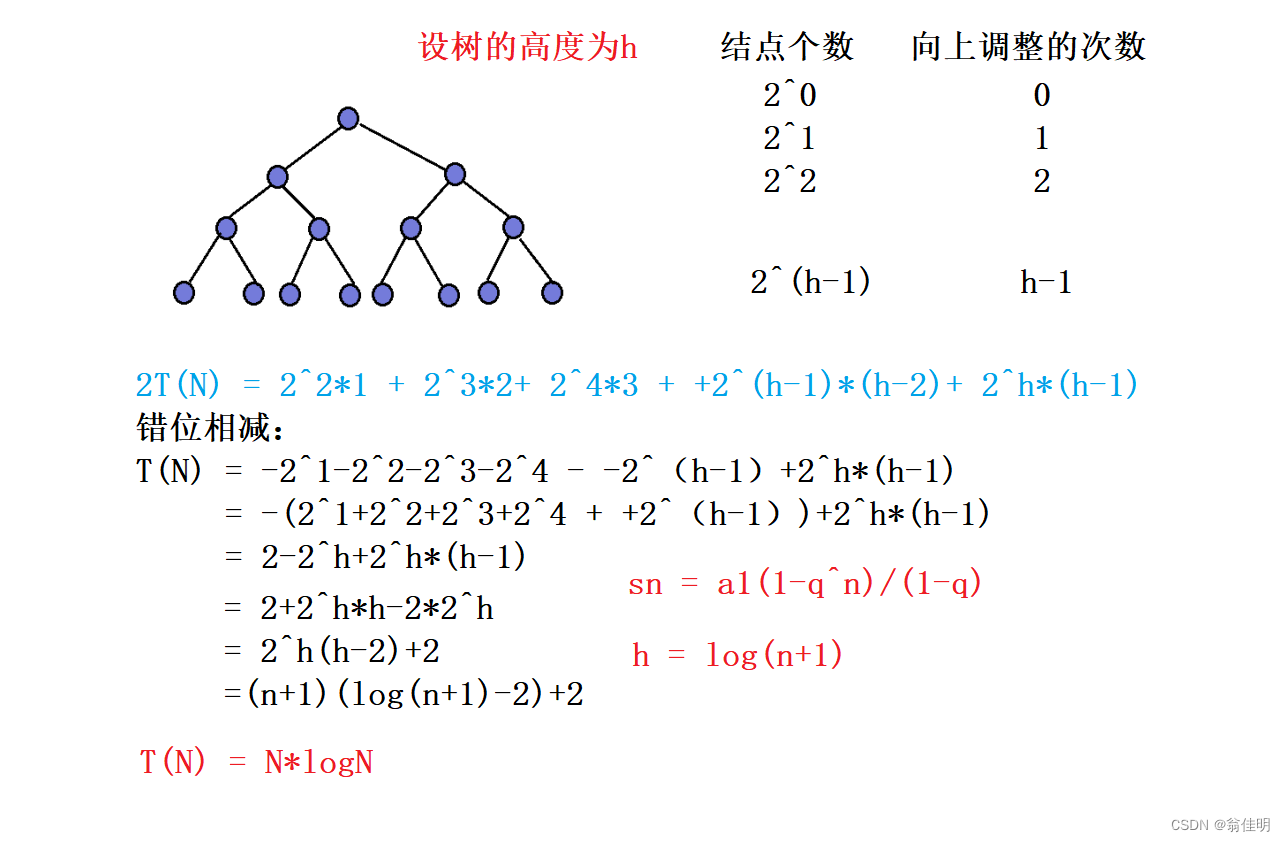
5.堆的删除

• 1.堆的删除，删除的是堆顶元素
• 2.将0下标和最后一个元素的下标进行交换，将堆中有效数据个数减少一个
• 3.对堆顶元素进行向下调整,只需要调整0下标的数

    /**
     * 删除堆顶
     */
    public void pop() {
        if (isEmpty()) {
            return;
        }
        swap(elem, 0, usedSize - 1);//堆顶和最后一个元素交换
        usedSize--;//删除一个元素
        shiftDown(0, usedSize);//向下调整
    }

    public boolean isEmpty() {
        return usedSize == 0;
    }

    private void swap(int[] array, int i, int j) {
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }

    public int peek() {
        if (isEmpty()) {
            return -1;
        }
        return elem[0];
    }

点击移步博客主页，欢迎光临~