1. 描述最大字段和的分治算法
题目

思路
判断最大子段和,可以用分治的思想,每次将序列一分为二,选择两个序列的最大子段和。
但是这里还有一种可能,就是子段可以横跨两个子序列,所以我们的最大子段和就是:
MAX(左边序列最大字段和,横跨两序列的最大子段和,右边序列的最大子段和)。
对于左右两边的最大子段和,可以用分治递归的方法来做,临界条件就是序列中只剩一个数了,这时候最大子段和就是这个数,而递归函数就是对左右两边分别求最大子段和(调用自身),而且还得求跨序列的最大子段和,取三者的最大值来返回。
那么怎么求跨序列的最大子段和呢?其实很简单,首先要对原来的大序列添加几个指针,开头的是指针l,最右边的是指针r,因为要分治,所以再设置一个中间的指针mid,此时序列就可以分为两个部分,分别是(l,mid)和(mid+1,r),这时候的跨序列子段,必须包含mid和mid+1这两个地方,当然也可以向左或向右延申,所以,我们只需要求出从mid开始向左延申的最大字段和,还有从mid+1开始向右延申的最大子段和,将两者相加,就能得到跨序列的最大子段和了。
思路很好理解,照着上面的描述画出图来就一目了然了。下面来看看代码实现吧。
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5;
int n, a[N];
int maxSum (int left, int right) {
if (left == right)
return a[left];
int mid = left + right >> 1;
int lmax = maxSum (left, mid);
int rmax = maxSum (mid + 1, right);
int sum = a[mid];
int clmax = a[mid];
for (int i = mid - 1; i >= left; i--) {
sum += a[i];
if (sum > clmax)
clmax = sum;
}
sum = a[mid + 1];
int crmax = a[mid + 1];
for (int i = mid + 2; i <= right; i++) {
sum += a[i];
if (sum > crmax)
crmax = sum;
}
int cmax = clmax + crmax;
int maxsum = max (cmax, max (lmax, rmax));
if (maxsum < 0)
maxsum = 0;
return maxsum;
}
int main () {
cin >> n;
for (int i = 0; i < n; i++)
cin >> a[i];
cout << maxSum (0, n - 1);
return 0;
}
2. 分析该算法的时间复杂度
分解子问题:O(1)
求解子问题:2T(n/2)
合并子问题:O(n)
故时间复杂度为T(n)=2T(n/2)+O(n)=nlogn
3. 对分治法的体会和思考
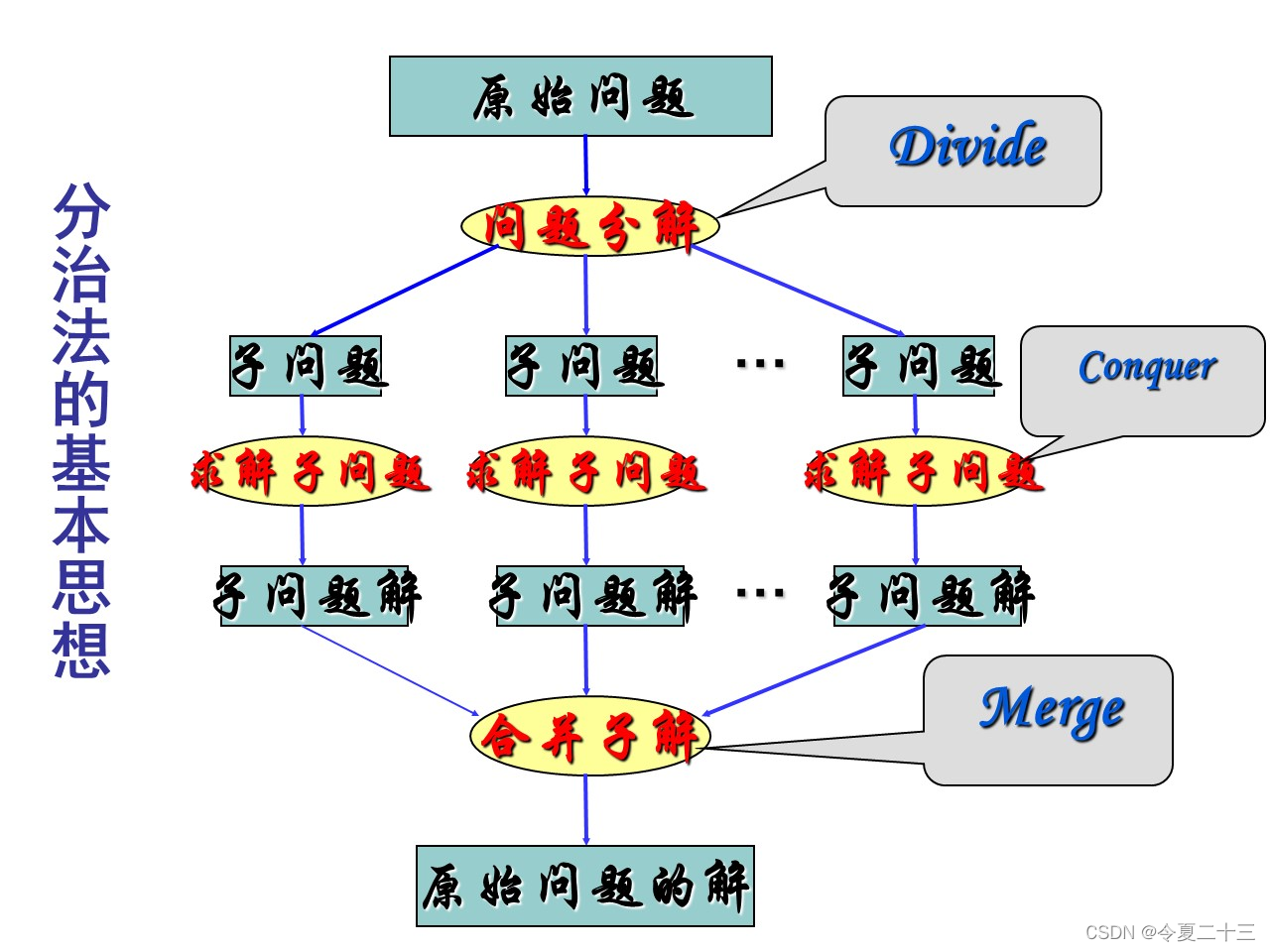
分治法的设计思想是,将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
其中的划分再击破,和递归的分解再解决异曲同工,其实同样用到了递归的思想,只不过分治法先分再治,最后还得合并。