文章目录
- 6.1 (1+1) 进化策略
- 6.2 1/5规则:推导
- 走廊问题
- 6.3 μ+1进化策略
- 6.4 μ+λ和(μ,λ)进化策略
- 6.5 自身自适应进化策略
- 协方差阵自适应CMA
6.1 (1+1) 进化策略
假设f(x)是随机向量x的函数,我们想要最大化适应度f(x).进化策略最早的算法初始化单个候选解并评价它的适应度,然后让候选解变异并评价变异后的个体的适应度.这两个候选解(父代和子代)中最好的那一个成为下一代的起点. 进化策略最初是为离散问题设计的,在离散搜索空间中采用小的变异很容易陷入局部最优值,所以后来把它改为在连续搜索空间中采用连续的变异,如算法6.1所示.
算法6.1被称为(1+1)-ES((1+1)进化策略),因为每代由1个父代和1个子代组成,并从父代和子代中选出最好的作为下一代的个体.(1+1)-ES也被称为二元进化策略,它与爬山策略非常相似,与种群规模为1的进化规划相同.下面的定理保证(1+1)-ES 最终能找到f(x)的全局最大值.

这个定理告诉我们,如果有足够时间,采用随机变异探索搜索空间最终能访问到整个搜索空间(在计算机的精度之内)并找到全局最优值。

在(1+1)-ES 算法6.1中的方差σ2是可调参数的值是一个折中.
- σ应该足够大以使变异能够在合理的时间内到达搜索空间的每一个区域.
- σ应该足够小以便找到在用户所需分辨率之内的最优解.
在进化策略向前推进时减小σ也许是适当的.在进化策略刚开始时,较大的σ值会允许进化策略进行粗粒度的搜索以靠近最优解.
在进化策略快要结束时,较小的σ值会让进化策略微调它的候选解并以更小的分辨率收敛到最优解.
算法6.1中的变异称为各向同性,因为x0的每个元素的变异方差相同,实际上,可以实施下面的非各向同性变异:

20%的变异能改进适应度函数f(x),如果变异成功率高于20%,则变异过小,带来的改进也小,收敛时间变长;如果变异成功率低于20%,则变异过大,带来的改进虽大但并不会经常发生,这样也会让收敛时间变长。
在(1+1)-ES 中,如果成功的变异与总变异的比值小于1/5,则应该减小标准差σ.如果这个比值大于1/5,则应该增大标准差.
让σ减小或增大的因子:
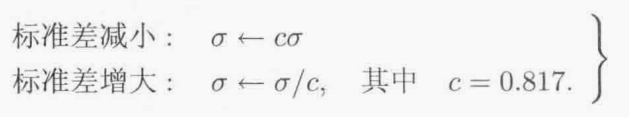
自适应(1+1)-ES需要定义移动窗口长度G.我们想让G足够大以便得到更准确的变异成功率,但G又不要大到令σ的自适应反应迟缓,建议如下:
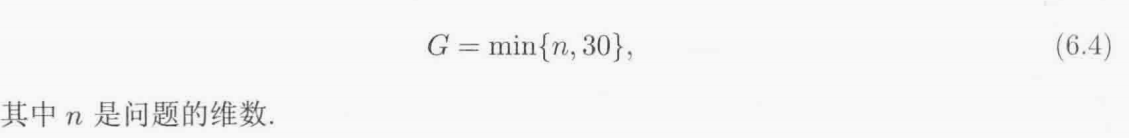


6.2 1/5规则:推导
走廊问题
假设一个n维最小化问题,其费用函数为f(x),其中x =[x1, x2,… ,xn] .本节聚焦在走廊问题上,它的域为
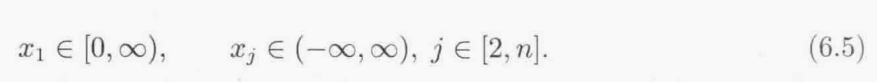
走廊问题的费用函数为:

进化策略中个体x0根据x1<–x0+r变异,这里r是n元随机向量,对于j属于[1,n],我们用x0j表示向量x0的第j个元素,x1j表示向量x1的第j个元素。
x0的每个元素的变异量从均值为零方差为σ2的高斯分布中选择,因此x1j的概率密度函数可以写成:
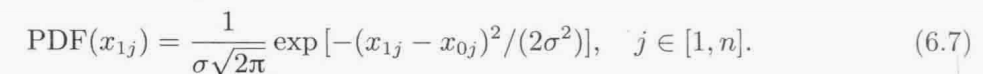
6.3 μ+1进化策略
最早对(1+1)-ES的一般化是(u+1)-ES.在(μ+1)-ES 中,每代用μ个父代,这里是由用户定义的参数.每个父代由相应的σ向量控制其变异的大小.父代组合形成单个子代,然后让子代变异.在μ个父代和这个子代中选出最好的μ个个体成为下一代的μ个父代.算法6.3是对它的总结.由于(μ+1)-ES 保留了每一代最好的个体,它奉行精英主义;也就是说,从一代到下一代,最好的个体绝不会变差.(μ+1)-ES也被称为稳态进化策略。由于在每一代的最后,从整个种群中只去掉一个个体,所以可以称这个策略为最差灭绝,它是适者生存的另一面。

重组的方式有很多:
-
离散性交
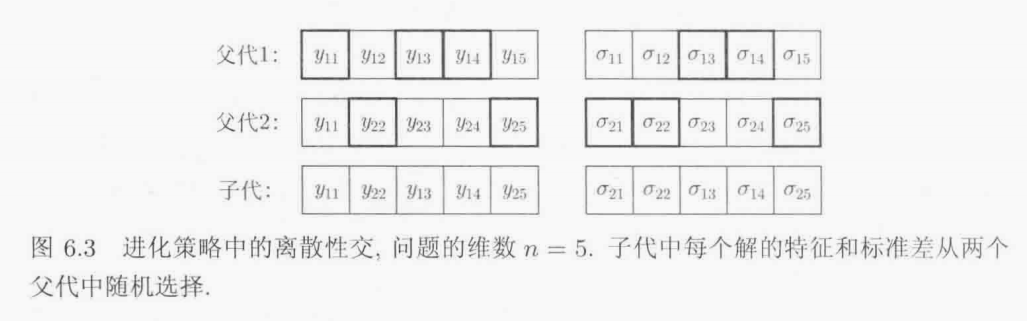
-
中间性交

-
全局交叉
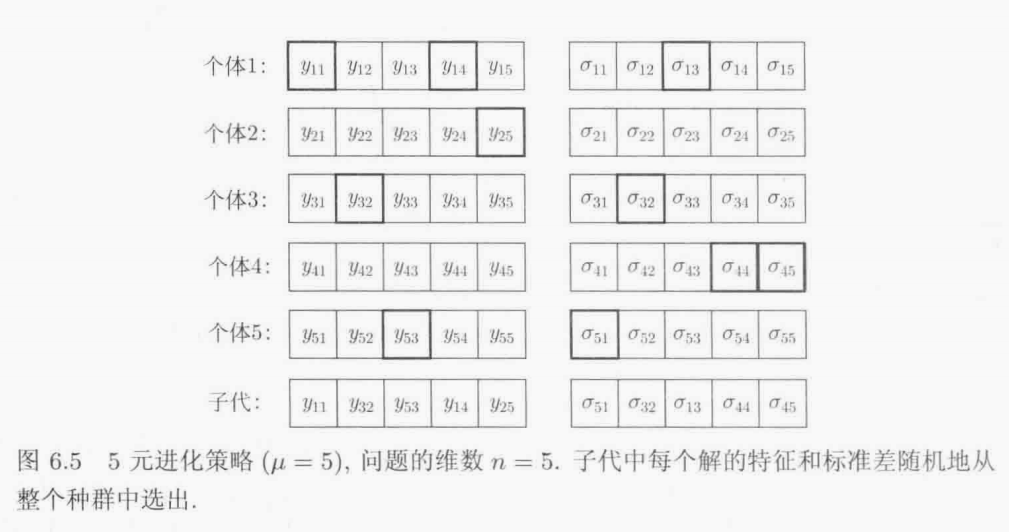
-
中间全局交叉
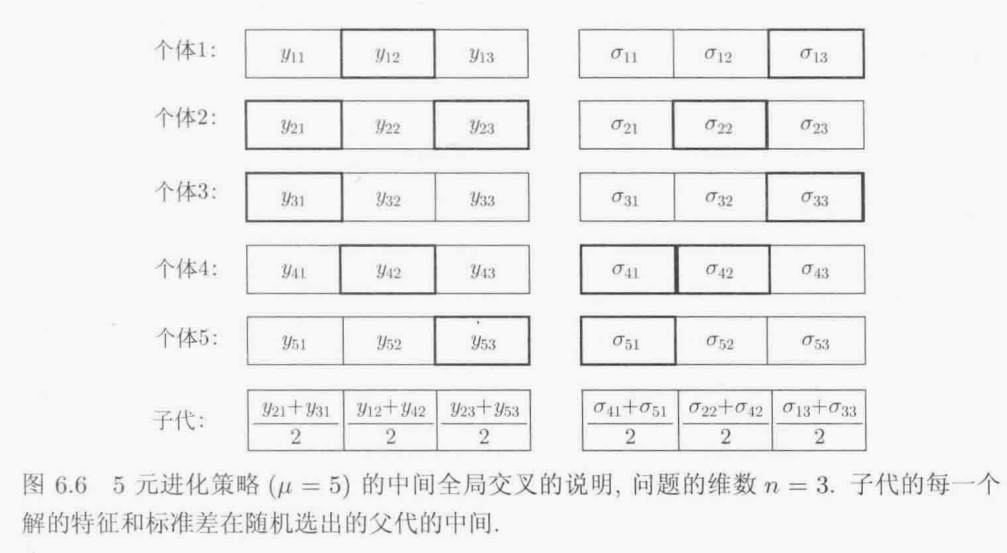
6.4 μ+λ和(μ,λ)进化策略
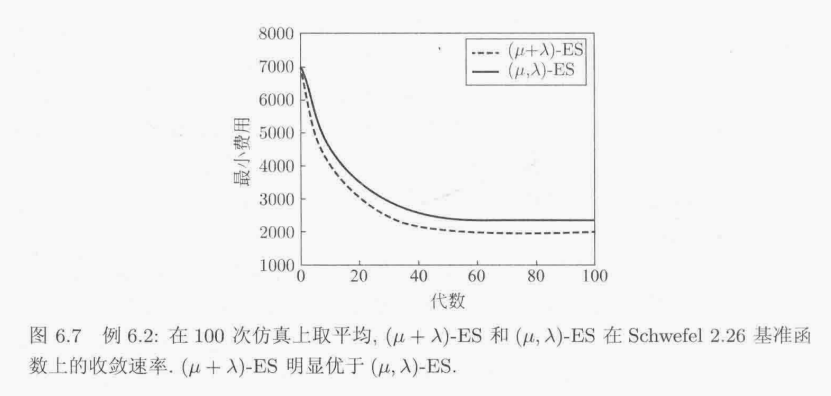
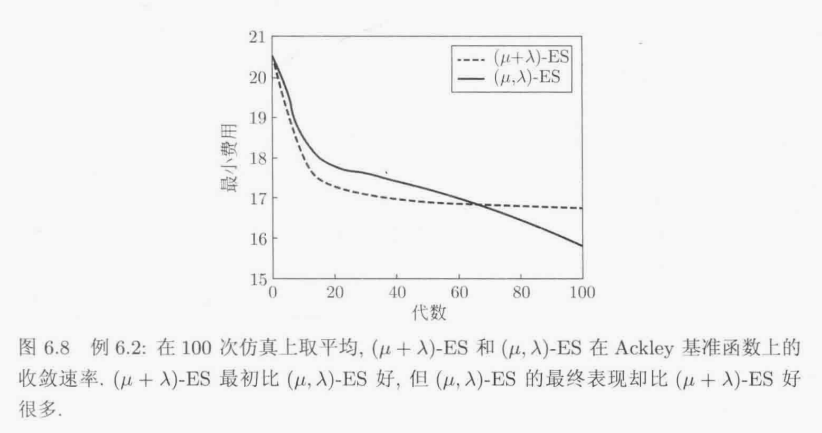
接下来对进化策略的一般化是(μ+λ)-ES.在(μ+λ)-ES 中,种群规模为u,每一代生成λ个子代.在生成子代之后,父代和子代总共有(μ+λ)个个体.在这些个体中选出最好的μ个作为下一代的父代.
另一个常用的进化策略是(μ,λ)-ES.在(μ,λ)-ES 中,从入个子代中选出最好μ个个体作为下一代的父代.换言之,μ个父代中无一生存到下一代;而是从λ个子代选出μ个个体的子集作为下一代的父代.在(μ,λ)-ES 中,我们需要保证所选的λ≥ μ.前一代的父代决不能生存到下一代,每一个个体的生命限定为一代.

6.5 自身自适应进化策略



协方差阵自适应CMA
CMA-ES的目标是尽可能好地用进化策略变异的分布与目标函数轮廓匹配。由此得到的匹配只有当目标函数为二次函数时会很完美,不过很多目标函数在它们的最优值附近都可以用二次函数近似。
CMA-ES的缺点在于复杂的自适应性策略以及复杂的可调参数设置。因此介绍CMA-ES的一个简化版本,它被称为协方差阵自身自适应进化策略CMSA-ES:在进化过程中学习搜索空间的形状,并调整变异方差。
学习参数:
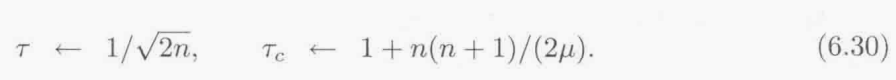


进化策略与遗传算法类似,但遗传算法最初是通过将候选解编码成位串来进化,而进化策略则总是在连续参数上操作.尽管遗传算法经常被用来处理连续参数,这两个算法还是存在哲学上的差别:进化策略的操作往往是在与问题陈述接近的表述形式上,而遗传算法的操作却往往在与问题最初陈述很不同的表示形式上.两个算法之间的另一个差别在于遗传算法强调重组,而进化策略强调变异.对于具体的优化问题,我们可以根据这些差别选择合适的算法.如果对于一个特别的问题,探索比开发更重要,我们可能得用进化策略.而如果开发更重要,就可能要用遗传算法.