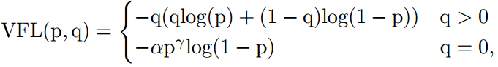两个有些难度的dp

中文题面，题意略

F 时间超限 II

一开始的思路想复杂了，想成了多重集的组合数学，二进制枚举肯定不行，dp也想的很复杂还错估时间复杂度。

补题的时候被题解的方法折磨好久，太抽象了。
这是官方题解

曾一度质疑是不是有问题 （官方的题解肯定没问题，是自己太笨看不懂），dp方程定义看起来是方案数又涉及时间，前面的时间乘上后，后面转移又用的加法，认为没有考虑到后面方案数也要乘上。但是用一份过了代码跑了一下后发现题解的dp算出来根本没错，但还是理解不了，果然还是自己太菜了（悲）。

这里介绍一种我自己的比较好理解的思路。

思路

我们考虑将方案数和时间分开考虑，枚举评测机 $i$ 和该评测机上测评了 $j$ 份代码，并且小M的代码也在其中，这样时间就确定了是 $t_{ij}$，只需要求出现这一情况的方案数即可。

如何求方案数？考虑到前 $1\sim i-1$ 个评测机上有不同情况，后 $i+1\sim n$ 个评测机上也有不同情况，两者相乘才是总的方案数，于是我们就对前后缀分别求一次dp，dp方程定义是：

后缀 $g[i][j]$：从后开始到 $i$ 为止的评测机共测评了 $j$ 份代码，并且小M的代码不在其中的方案数。

g[n + 1][0] = 1;
for(int i = n; i >= 1; i --){
    int suf = min(m, pre[n] - pre[i - 1]); // 最大评测题数
    for(int j = 0; j <= suf; j ++){ // 枚举题数
		for(int p = 0; p <= min(k[i], j); p ++){ // 枚举这个评测机上的题数
			g[i][j] = (g[i][j] + g[i + 1][j - p]) % mod;
		}
    }
}

前缀 $f[i][j]$：前 $i$ 个评测机共评测了 $j$ 份代码，并且小M的代码在其中的总方案数。
在求前缀的代码中就可以边求方案数，边把答案算进总答案了，转移和后缀其实一模一样，直接看总代码就好了。

代码

#include <bits/stdc++.h>
using namespace std;

#define ll long long
const int N = 2e3 + 10, M = 1e4 + 10, mod = 1e9 + 7;

vector<int> v[N];
int n, m;
int k[N], pre[N];


ll f[N][M]; // 前i台评测机，总共评测了j个题目，指定代码评测了的方案数
ll g[N][M]; // 从后往前直到第i台评测机，总共评测了j个题目，指定代码没有评测的方案数
ll sum[M][2]; 
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);

    cin >> n;
    for(int i = 1; i <= n; i ++){
        cin >> k[i];
        pre[i] = pre[i - 1] + k[i];
        for(int j = 1, t; j <= k[i]; j ++){
            cin >> t;
            v[i].push_back(t);
        }
    }

    cin >> m;
	g[n + 1][0] = 1;
    for(int i = n; i >= 1; i --){
        int suf = min(m, pre[n] - pre[i - 1]); // 后缀最大评测题数
        for(int j = 0; j <= suf; j ++){ // 枚举题数
			for(int p = 0; p <= min(k[i], j); p ++){ // 枚举这个评测机上的题数
				g[i][j] = (g[i][j] + g[i + 1][j - p]) % mod;
			}
        }
    }

    ll ans = 0;
    f[0][0] = 1;
    for(int i = 1; i <= n; i ++){
        int p = min(m, pre[i]); // 前缀最大评测数
        for(int j = 0; j <= p; j ++){ // 枚举题数
        	for(int q = 0; q <= min(k[i], j); q ++){ // 枚举这个评测机评测的代码
                f[i][j] = (f[i][j] + f[i - 1][j - q]) % mod;
				// 总时间 = 前缀方案数 * 后缀方案数 * 时间
                if(q) ans = (ans + f[i - 1][j - q] * g[i + 1][m - j] % mod * v[i][q - 1] % mod) % mod;   
            }
        }
    }  
    
    cout << ans << "\n";
    
    return 0;
}

待补

H 玻璃球

思路

代码