1.小熊买糖果
【问题描述】
小熊去到商店,选择了一种它非常喜欢的糖果,其单价为 k 元,假定商店里有无穷多的这种糖果。
它的父亲允许它花费任意多的10元硬币和一个 r 元硬币去购买,但不能找零,请帮助小熊确定它能购买的最少数量的糖果是多少?
【输入形式】
输入为一行两个整数 k 和 r (1≤ k ≤1000,1≤ r ≤9),分别表示糖果的价格以及小熊手里的单独硬币的币值。
【输出形式】
输出为一个数,表示小熊在不找零的情况下所能购买糖果的最小数量。
【样例输入1】
117 3
【样例输出1】
9
【样例输入2】
10 3
【样例输出2】
1
//小熊买糖果
//小熊去到商店,选择了一种它非常喜欢的糖果,其单价为 k 元,假定商店里有无穷多的这种糖果。
//
// 它的父亲允许它花费任意多的10元硬币和一个 r 元硬币去购买,但不能找零,请帮助小熊确定它能购买的最少数量的糖果是多少?
#include <iostream>
using namespace std;
int getCandy(int, int);
int main()
{
int k, r;
cin>>k>>r;
int result=getCandy(k,r);
cout<<result<<endl;
return 0;
}
int getCandy(int k,int r){
int res=1;
int s=k;
while(s%10!=0 && (s-r)%10!=0){ //要么没用零钱全是10,要么用了零钱
s+=k;
res+=1;
}
return res;
} 2.最大公约数和最小公倍数
【问题描述】
从键盘输入两个正整数,求他们的最大公约数和最小公倍数。
【输入形式】
输入为一行,两个正整数
【输出形式】
输入为一行,表示这两个正整数的最大公约数和最小公倍数
【样例输入】
15 125
【样例输出】
5 375
//最大公约数和最小公倍数
//从键盘输入两个正整数,求他们的最大公约数和最小公倍数。
#include <iostream>
using namespace std;
int gcd(int,int);
int lcm(int,int);
int main()
{
int x,y;
cin>>x>>y;
cout<<gcd(x, y)<<" "<<lcm(x,y)<<endl;
return 0;
}
int gcd(int u, int v)
{
if(u<v){
int tem=u;
u=v;
v=tem; //大的除以小的
}
int m=u%v;
while(m!=0){
u=v;
v=m; //辗转相除法
m=u%v;
}
return v;
}
int lcm(int u,int v)
{
//最小公倍数等于两数乘积除以最大公约数
return u*v/gcd(u,v);
}3.我爱数学,我爱编程,我更爱多文件编程
【问题描述】
从键盘输入任意多个正整数,判断其中有多少个素数和回文数?
【输入形式】
输入任意多个正整数,输入使用ctrl^Z结束。
【输出形式】
输出为两个整数,分别表示输入的若干个数中,素数、回文数的个数。
【样例输入】
11 121 7
【样例输出】
2 3
#include"judge.h"
//从键盘输入任意多个正整数,判断其中有多少个素数和回文数?
bool prime(int a){
if(a<2){
return false;
}else if(a==2){
return true;
}
for(int i=2;i<=a/2+1;i++){
if(a%i==0){
return false;//是不是素数
}
}
return true;
}
bool plalindrome(int a){
int res=0;
int t=a;
while(a>0){
int y=a%10; //是不是回文数
a/=10;
res*=10;
res+=y; //直接反转数字
}
if(res==t){
return true;
}else{
return false;
}
}
4.杨辉三角
【问题描述】
输入层数 n,打印 n 层杨辉三角
【输入形式】
输入为一行一个整数 n
【输出形式】
输出 n 层杨辉三角
【样例输入】
5
【样例输出】
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
提示:杨辉三角的每一行对应为二项式系数,且有公式
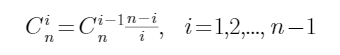
#include"yang.h"
#include<iostream>
//输入层数 n,打印 n 层杨辉三角
using namespace std;
void PrintBlank(int num){
for(int i=1;i<=num;i++){
cout<<" "; //打印空格,第一个数前面的
}
}
void PrintCombine(int n){
n-=1;
int *arr=new int[n+1];
arr[0]=1;
cout<<arr[0]<<" ";
for(int i=1;i<=n;++i){
arr[i]=arr[i-1]*(n-i+1)/i; //利用杨辉三角的每一行对应为二项式系数,且有公式
cout<<arr[i]<<" ";
}
}