在二维矩阵/数组中查找元素 Leetcode74, Leetcode240

news2024/11/27 9:52:43

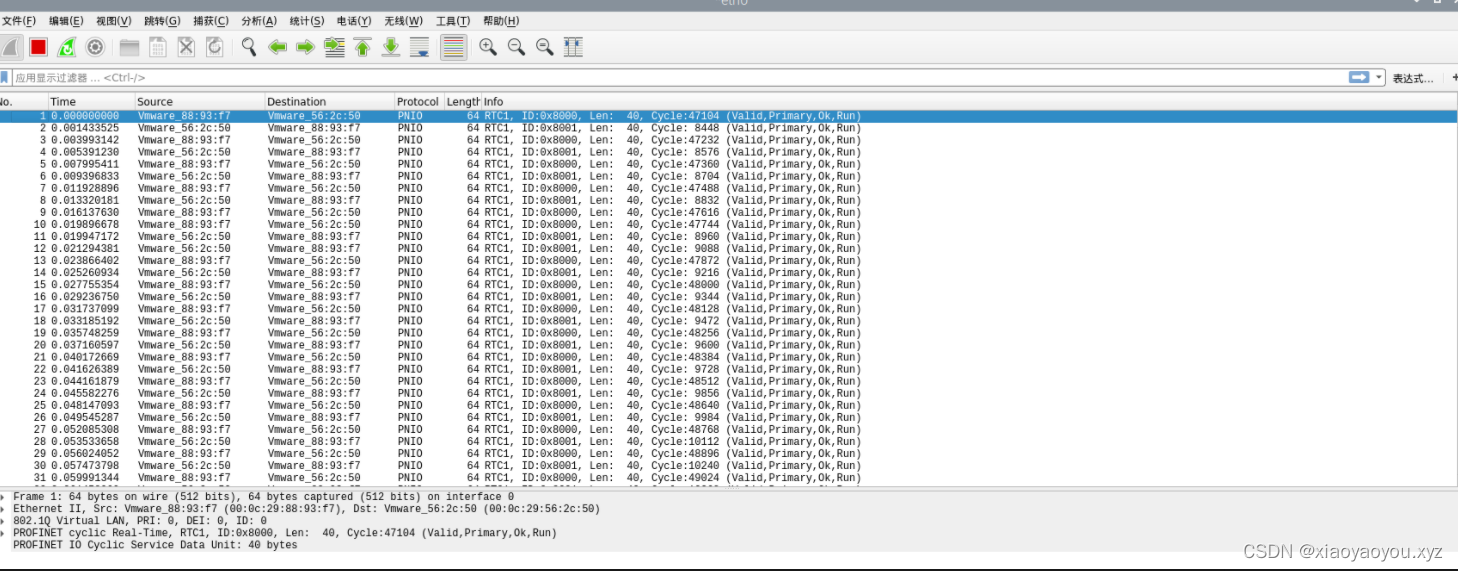
这一类题型中二维数组的元素取值有序变化，因此可以用二分查找法。我们一起来看一下。

一、Leetcode 74

Leetcode 74. 搜索二维矩阵这道题要在一个二维矩阵中查找元素。该二维矩阵有如下特点：

每行元素从左到右按非递减顺序排列。
每行的第一个元素 > 前一行的最后一个元素。

也就是说，这种二维数组的元素逐行、逐列递增变化，如下图所示，沿箭头方向元素值递增：

在这里插入图片描述

方法一：做两次二分查找。

先在第一列中查找值为 target 的元素所在行。
再在这一行中查找值为 target 的元素所在列。

在这两步中，难点在于第一步确定 target 所在行。以图中的示例矩阵为例，要寻找 3，如何定位到 3 所在行呢？在第一列的元素中，3 所在行的第一列元素 1 是小于 3 的元素中最接近 3 的元素，这就是第一步的思路：在第一列元素中查找小于等于 target、且最接近 target 的元素。这里可以用 Leetcode 69 所使用的方法（欢迎阅读文章：二分查找法搜寻元素 Leetcode35, Leetcode69，其中详细介绍了这类问题的两种解决方法，本文采用了其中一种方法。）

相应的 Python 代码和注释为：

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        # 第一步：查找元素所在行
        low, high = 0, len(matrix) - 1
        while low <= high:
            mid = low + (high - low) // 2
            # 注意：这里是在第 1 列查找，
            # mid元素索引为 matrix[mid][0]。
            if matrix[mid][0] == target:
                return True
            elif matrix[mid][0] > target:
                high = mid - 1
            else:
                low = mid + 1
        # 确定元素所在行(row)
        row = high

        # 第二步：查找元素所在列
        low, high = 0, len(matrix[0]) - 1
        while low <= high:
            mid = low + (high - low) // 2
            # 注意：这里是在第 row 行查找，
            # mid元素索引为 matrix[row][mid]。
            if matrix[row][mid] == target:
                return True
            elif matrix[row][mid] > target:
                high = mid - 1
            else:
                low = mid + 1

        return False

方法二：把二维矩阵看作一个一维数组处理。

因为矩阵的元素是按升序排列，我们在处理时可以把它想象成连续的一维序列，就像上图示例矩阵中的元素，在脑子里把它“拼接”成一个连续的一维数组，[1,3,5,7,10,11,16,20,23,30,34,60]，在这个升序数组里查找元素很容易。

但是，这个一维数组索引只是我们为了解决问题做的设想，实际中矩阵元素是以二维数组形式存储的，因此每次索引元素值时还需要一个操作：把（设想的）一维数组索引换算回（实际的）二维数组索引。

相应的 Python 代码和注释为：

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        # 求 mxn 矩阵的维度大小
        m = len(matrix)
        n = len(matrix[0])
        
        # 按“一维”有序数组处理
        length = m*n
        low, high = 0, length - 1
        while low <= high:
            mid = low + (high - low) // 2
            
            # 关键：索引时要把（设想的）一维数组索引换算回（实际的）二维数组索引。
            mid_row = mid // n
            mid_col = mid % n
            mid_val = matrix[mid_row][mid_col] 
            
            if mid_val == target:
                return True
            elif mid_val > target:
                high = mid - 1
            else:
                low = mid + 1
        return False

方法二实现起来比方法一更简洁，但是我在 Leetcode 运行代码时发现方法二比方法一的耗时大。

二、Leetcode 240

Leetcode 240. 搜索二维矩阵 II 这道题也是在二维矩阵中查找元素。不同的是，这里的二维矩阵有如下特点：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

下图所示为一个示例矩阵：

在这里插入图片描述

这道题的巧妙之处在于中点 mid 的选择。

根据给定矩阵的升序排列特点，一个元素位于第 i 行、第 j 列，则该元素所在行第 0 ~ ( j - 1 ) 列的元素都比它小；该元素所在列第 ( i + 1 ) ~ ( m - 1 ) 行的元素都比它大。具体来说，以上图的示例矩阵为例，如绿色箭头标识所示，以圆圈中的元素 8 为中点，[ 2, 5, 8, 9, 14, 23 ] 这些元素就构成了一个升序排列的数组。也就是说，以第 i 行、第 j 列的元素为直角，其所在行和列元素构成的倒 “L” 形状序列是一个有序数组，而在直角的这个元素就是数组的中点。在这个数组中可以用二分查找：比较中点的元素与目标值 target 的大小决定下一步的寻找范围。如果该元素大于 target，就往左移一列：j - 1。如果该元素小于 target，就往下移一行：i + 1。

应该从哪里开始呢？选择右上角的元素（第 0 行，(n-1) 列）做为起始 mid 元素，逐步推进到左下角元素。时间复杂度是 O(m+n)。这一点您可以试一下，如果要找的元素位于左下角，正好要走 m+ n 步。

相应的 Python 代码为：

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])
        i, j = 0, n - 1
        while i < m and j >= 0:
            if matrix[i][j] == target:
                return True
            elif matrix[i][j] > target:
                j -= 1
            else:
                i += 1
        return False