标题：Compensation of Long-Term Memory Effects on GaN HEMT-Based Power Amplifiers

来源：IEEE TRANSACTIONS ON MICROWAVE THEORY AND TECHNIQUES

• DPD：数字预失真（Digital Pre-Distortion）
• RF PA：射频功率放大器（Radio Frequency Power Amplifier）

  本文分为三个主要部分。首先，在第二部分，论文将开发和支持用于非线性失真补偿的 DPD 模型结构。在第三部分，论文将开发辅助模型结构，用于开发的 DPD。最后，第四部分展示了如何使用开发的模型来补偿几种先进的 RF PA，并将获得的结果与使用先进 DPD 模型获得的结果进行比较。

DPD模型结构

  在开发 DPD 模型结构时，可以首先假设 RF PA 没有长期记忆行为。在这种情况下，可以使用任何典型的 DPD 模型来实现所需的线性度。从经验来看，GMP 模型通常能够很好地胜任这一角色，因此将以其为例进行说明
$$\begin{array}{rl}\tilde{\mathrm{y}}(n)& =\sum _{p=0}^P\sum _{m=0}^M{\tilde{h}}_p(m,0)\tilde{x}(n-m)|\tilde{x}(n-m){|}^p\\ & +\sum _{p=1}^K\sum _{m=0}^M\sum _{l=1}^L{\tilde{h}}_p(m,l)\tilde{x}(n-m)|\tilde{x}(n-m-l){|}^k\\ & +\sum _{p=1}^K\sum _{m=0}^M\sum _{l=1}^L{\tilde{h}}_p(m,-l)\tilde{x}(n-m)|\tilde{x}(n-m+l){|}^k.\end{array}(1)$$
  在 (1) 中，波浪号用于识别复数变量。$\tilde{x}\left(n\right)$是模型输入端的复包络，$\tilde{y}\left(n\right)$ 是模型输出端的复包络，$\tilde{h}$是模型参数，三元组 (K, M, L) 定义了模型结构，n 是采样时间。
  由于本文的重点是补偿长期记忆行为，文中假设 (1) 中的 GMP 模型确实可以在没有这些影响的情况下使 RF PA 线性化。
  当长期记忆行为被激发时，RF PA 的特性会随着时间的推移缓慢变化，长期记忆行为可以通过一组随时间变化的状态变量$\vec{\alpha }\left(n\right)$来表征。对于该状态向量的每个值，RF PA 都会发生细微的变化。事实上，只要 PA 的常见时间常数和与长期记忆效应相关的时间常数相差很大，文中假设对于长期状态向量的每个状态，我们都有一个稍有不同的 PA，可以使用 (1) 中的 GMP 模型来校正，只需略微改变其系数值。因此，文中假设能够访问这个隐藏的状态向量，文中可以使用以下方法来描述一个预失真器：
$$\begin{array}{rl}& \tilde{\mathrm{y}}(n)\\ & =\sum _{p=0}^P\sum _{m=0}^M{\tilde{h}}_p(m,0,\vec{\alpha }(n))\tilde{x}(n-m)|\tilde{x}(n-m){|}^p\\ & +\sum _{p=1}^K\sum _{m=0}^M\sum _{l=1}^L{\tilde{h}}_p(m,l,\vec{\alpha }(n))\tilde{x}(n-m)|\tilde{x}(n-m-l){|}^k\\ & +\sum _{p=1}^K\sum _{m=0}^M\sum _{l=1}^L{\tilde{h}}_p(m,-l,\vec{\alpha }(n))\tilde{x}(n-m)|\tilde{x}(n-m+l){|}^k.\end{array}(2)$$
  在 (2) 中，利用长期记忆行为的先验知识来避免修改底层的补偿模型。在使用 (2) 式的表达时，需要回答两个问题：第一，原始模型的系数随着新变量的变化而如何变化？第二，如何访问隐藏的长期状态向量？
  可以采用多种非线性展开来解决第一个问题。必须注意确保系数的数量不会过多增加。作为初步近似，可以将系数展开为状态向量的线性函数，如 (3) 式所示。这种展开将使系数的数量增加 KN 个，其中 K 是长期状态变量的数量，N 是系数的数量。
$${\tilde{h}}_p(m,l,\vec{\alpha }(n))\cong ({\tilde{h}}_p(m,l)+\frac{\Delta {\tilde{h}}_p(m,l)}{\Delta \vec{\alpha }(n)}\vec{\alpha }(n)).(3)$$
  在论文的方法中，将长期状态变量的数量限制为两个：一个描述由于热效应引起的的变化，α_Th(n)；另一个描述由于电子俘获效应引起的的变化，α_Trap(n)。为了访问这些状态变量，我们研究了这些效应在器件层面的行为，并将其表示为依赖于输入包络的数字模型。
  使用所描述的方法，DPD 模型结构如图 1 所示，其中 GMP 系数线性依赖于控制信号。请注意，控制信号不必跟踪温度和俘获电荷的绝对值。事实上，由于模型会定期更新，因此只需跟踪与平均值的偏差。观察 (3)，可以看出平均值可以包含在 ${\tilde{h}}_p(m,l)$ 项中。此外，控制信号的任何缩放都是无关紧要的，因为相应的系数也在回归过程中被提取。

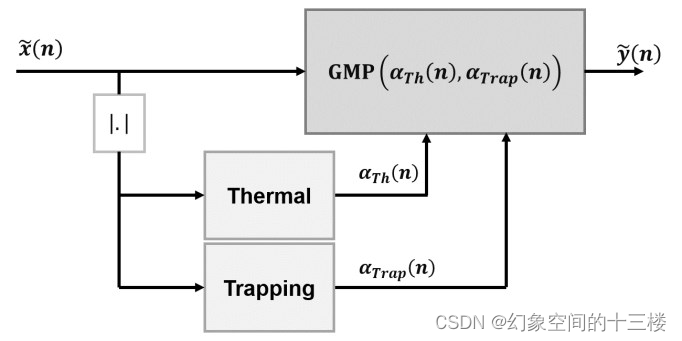
系数提取

  假设控制信号 α_Th(n) 和 α_Trap(n) 是已知的，则模型在参数上保持线性。因此，可以将典型的最小二乘法提取方法应用于新的回归矩阵，如 (4) 式所示，其中 X_GMP 是原始的 GMP 回归矩阵，A_th 是以向量形式表示的热控制信号，A_Trap 是以向量形式表示的捕获控制信号，⊗ 是克罗内克积。
$$X=[X_{\mathrm{GMP}}{A}_{\mathrm{th}}\otimes X_{\mathrm{GMP}}{A}_{\mathrm{Trap}}\otimes X_{\mathrm{GMP}}].(4)$$

基于物理的辅助模型

热模型

  器件的温度取决于晶体管上耗散的功率。这种热机制可以解释为一个热流源，它将通过结面、封装和散热片消散到环境中，如图 2 所示。每个温度界面都会给热系统施加一个时间常数。然而，RF PA 的封装和散热片具有很高的时常数，并且在 RF PA 运行时会趋于稳定在一个恒定的温度；因此，只有器件的结面需要考虑。结面处的温度取决于晶体管材料的热容和导热率。

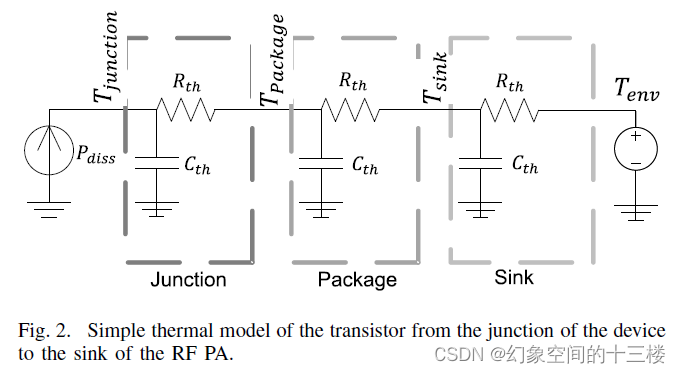
  对于 GaN HEMT，热效应的影响已被证明在器件建模和 RF PA 设计中具有重要意义，不仅是静态温度，还有相关的动态特性。
  结面温度模型可以写成 (5) 式所示的连续时间形式。由于假设封装温度稳定在某一恒定值，因此 T_package 项对论文的目的无关紧要。
$$T_{\mathrm{junction}}+R_{\mathrm{th}}{C}_{\mathrm{th}}\frac{d{T}_{\mathrm{junction}}}{dt}=R_{\mathrm{th}}{P}_{\mathrm{diss}}+T_{\mathrm{package}}.(5)$$
  在 (5) 式中，变量与图 2 相关：T_junction 是结面温度，T_package 是封装温度，R_th 是热阻，C_th 是热容。

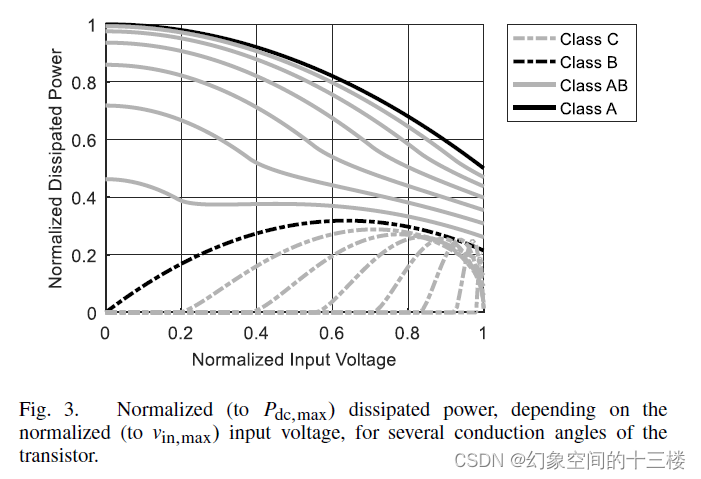
  耗散功率可以近似为输入包络的函数，通常不是其平方值，这取决于工作类型。方程 (6) 显示了用于最佳功率负载的归一化输入包络的耗散功率公式，该公式取决于导通角 θ。图 3 显示了耗散功率曲线，该曲线取决于输入幅度和不同的导通角。
$$\begin{array}{rl}\frac{P_{\mathrm{DC}}}{P_{\mathrm{DC}},\max }& =\frac{1}{\pi }\left(\frac{{\nu }_{\mathrm{in}}}{{\nu }_{\mathrm{in},\max }}\sin \left(\frac{\xi }{2}\right)-\cos \left(\frac{\theta }{2}\right)\frac{\xi }{2}\right)\\ \frac{P_L}{P_{\mathrm{DC},\max }}& =\frac{r_L}{2{\pi }^2}(\frac{{\nu }_{\mathrm{in}}}{2{\nu }_{\mathrm{in},\max }}(\xi +\sin (\xi ))-2\cos \left(\frac{\theta }{2}\right)\sin \left(\frac{\xi }{2}\right){)}^2\\ \frac{P_{\mathrm{diss}}}{P_{\mathrm{DC},\max }}& =\frac{P_{\mathrm{dc}}}{P_{\mathrm{DC},\max }}-\frac{P_L}{P_{\mathrm{DC},\max }}\\ r_L& =\frac{2\pi }{\theta -\sin \left(\theta \right)},\text{ normalized to 1 }\Omega \\ \xi & =\{\begin{array}{l}2{\cos }^{-1}\left(\frac{1}{\frac{V_{\mathrm{in}}}{V_{\mathrm{in},\max }}}\cos \left(\frac{\theta }{2}\right)\right)\frac{V_{\mathrm{in}}}{V_{\mathrm{in},\max }}\ge |\cos \left(\frac{\theta }{2}\right)\\ \pi \left(1+\mathrm{sign}(\theta -\pi )\right)\frac{V_{\mathrm{in}}}{V_{\mathrm{in},\max }}<\left|\cos \left(\frac{\theta }{2}\right)\right|.\end{array}\end{array}(6)$$
  在 (6) 式中，v_in 是输入电压，P_L 是输出功率，P_dc 是消耗功率，P_diss 是耗散功率，θ 是满功率时的导通角，ξ 是有效导通角。
  通常，单端射频功率放大器中的晶体管将偏置在接近B类工作状态。在这种情况下，归一化功率耗散曲线可以写成（7）式所示的形式，这大大简化了耗散功率表达式。
$$\frac{P_{\mathrm{diss}}}{P_{\mathrm{DC},\max }}=\frac{{\nu }_{\mathrm{in}}}{{\nu }_{\mathrm{in},\max }}-\frac{\pi }{4}{\left(\frac{{\nu }_{\mathrm{in}}}{{\nu }_{\mathrm{in},\max }}\right)}^2.(7)$$
  综合所有这些信息，可以利用双线性z变换将模型转换为数字低通等效域（LPE），以适应动态效应。这将产生热辅助模型，如（8）式所示。为了简洁，（8）式已被缩放，并且常数项已被移除。如前所述，这是可以做到的，因为回归过程将恢复这些参数。
$$\begin{array}{rl}(1-2f_s{\tau }_{\mathrm{th}})& a_{\mathrm{th}}(n-1)+(1+2f_s{\tau }_{\mathrm{th}})a_{\mathrm{th}}(n)\\ & =f(|x(n-1)|)+f(|x(n)|)\\ f(|x(n)|)& =|x(n)|-\frac{\pi }{4}|x(n){|}^2.\end{array}(8)$$
  在 (8) 式中，f_s 是采样频率，${\tau }_{\mathrm{th}}=R_{\mathrm{th}}{C}_{\mathrm{th}}$ 是热时间常数。
  热辅助模型只依赖于一个参数，即热时间常数 ${\tau }_{\mathrm{th}}$。

电子俘获模型

  GaN HEMTs中的电子俘获效应在栅极和漏极处都有观察到，分别称为栅极滞后和漏极滞后。在这两种效应中，栅极滞后在当前的GaN HEMT世代中已被大部分解决或显著降低。漏极滞后效应仍然存在，并对晶体管行为产生明显的影响，其中最显著的是在工作时会自偏压。
  电子俘获效应的特点是具有两个非常不同的相关时间常数。一个与电荷俘获有关，另一个与去俘获有关。这些不同的时间常数会导致与传统上在常见物理系统中观察到的行为不同的行为。

  用于在仿真模型中跟踪俘获电荷的一种提出的系统如图4所示。二极管充当理想器件，当电压为正时表现为短路，当电压为负时表现为开路。两个不同的电阻可以设置不同的充电和放电时间常数。电荷模型由以下公式描述：
$$\{\begin{array}{l}{R}_{2}C\frac{d{\nu }_c(t)}{dt}=({\nu }_d(t)-{\nu }_c(t)){\nu }_c(t)\le {\nu }_d(t)\\ (R_1+R_2)C\frac{d{\nu }_c(t)}{dt}=({\nu }_d(t)-{\nu }_c(t)){\nu }_c(t)>{\nu }_d(t).\end{array}(9)$$
  在(9)式中，变量与图4相关，v_d是晶体管漏极电压，v_c是电容上的电压，它直接与积累的电荷相关。
  俘获电荷模型的输入是真实的漏极电压，而不是包络幅度。然而，直接在该模型中使用包络幅度可以很好地近似真实结果。为简化起见，本文使用了直接转换为数字LPE域（使用双线性变换）的表达式，如下所示：
$$\{\begin{array}{l}(1-2f_s{\tau }_d){\alpha }_{\text{Trap}}(n)+(1+2f_s{\tau }_d){\alpha }_{\text{Trap}}(n-1)\\ =|x(n-1)|+|x(n)|,{\alpha }_{\text{Trap}}(n)>|x(n)|\\ (1-2f_s{\tau }_u){\alpha }_{\text{Trap}}(n)+(1+2f_s{\tau }_u){\alpha }_{\text{Trap}}(n-1)\\ =|x(n-1)|+|x(n)|,{\alpha }_{\text{Trap}}(n)\le |x(n)|\end{array}(10)$$
  在 (10) 式中，|x(n)| 是输入信号的包络幅度，α_Trap(n) 是俘获电荷，τ_up = R₁C 是充电时间常数，τ_d = R₂C 是放电时间常数，f_s 是采样频率。该模型有两个待求参数，即充电和放电时间常数。
  请注意，俘获模型的输入实际上应该是晶体管的输出，而不是输入。这需要一个反馈模型结构。因此，最初，PA 输出与其输入之间会存在显着差异。但是，随着 PA 变得线性化，输出会越来越接近输入，这使得这是一个有效的近似。

辅助模型拟合

AM/AM代表幅度调制对幅度的影响，而AM/PM代表幅度调制对相位的影响
  如前所述，DPD模块的输出对来自辅助模型的控制信号呈非线性依赖关系。此外，辅助模型具有无限脉冲响应滤波器，这增加了参数提取的难度。
  为了提取这些模型的参数，论文开发了一种基于残差观测（稍后定义）的新技术。这些参数只提取一次，并用于多个不同的信号。这是使用具有物理意义的模型的优势，因为模型参数不会改变，除非器件本身发生变化。
  为了提取辅助模型参数，需要对其应产生的信号进行表示。但是，如前所述，我们无法直接测量器件的内部温度和俘获电荷。尽管如此，仍然可以获得这些信号的间接测量。如前所述，RF PA 特性会随着温度和俘获电荷的变化而变化。当 PA 用信号激励时，可以在输出基频包络中观察到这种缓慢的变化。但是，它将与输入信号产生的快得多变化混合在一起，这些变化明显占主导地位。然后必须对输出信号进行处理以提取所需信息。输出信号可以用 (11) 式中的形式表示，其中 a(·) 是 AM/AM，φ(·) 是 AM/PM。
$$\begin{array}{rl}\tilde{y}(n)& =a(\tilde{x}(n),\tilde{x}(n-1),\dots ,{\alpha }_{\text{Trap}}(n),{\alpha }_{\text{Th}}(n))\exp (j/\tilde{x}(n))\\ & \times \exp (j\varphi (\tilde{x}(n),\tilde{x}(n-1),\dots ,{\alpha }_{\text{Trap}}(n),{\alpha }_{\text{Th}}(n))).\end{array}(11)$$
  为了提取温度和俘获信号对输出的影响，我们首先用输入信号的静态函数（12式）来近似输出信号。为了实现这一点，我们使用最小二乘法来提取一个无记忆多项式。
$${\tilde{y}}_a(n)=a_a(|\tilde{x}(n)|)\exp (j{\varphi }_a(|\tilde{x}(n)|))\exp (j\angle \tilde{x}(n)).(12)$$
  在方程（12）中，${\tilde{y}}_a$是无记忆近似，$a_a(\cdot )$是无记忆AM/AM，${\varphi }_a(\cdot )$是无记忆AM/PM。
  在获得这个无记忆近似之后，论文计算如下所示的残差：
$$\begin{array}{c}r(n)=a(\tilde{x}(n),\tilde{x}(n-1),\dots ,{\alpha }_{\mathrm{Trap}}(n),{\alpha }_{\mathrm{Th}}(n))-a_a(\tilde{x}(n))\\ G_r(n)=\frac{r(n)}{a_a(\tilde{x}(n))}.(\begin{array}{c}13\end{array})\end{array}$$
  (13) 式中的残差表述衡量了与静态增益的偏差。因此，我们期望它具有缓慢的热和俘获行为，但也具有更快的 PA 动态分量，这些分量应该由 GMP 模型捕获。为了去除这些快速分量，使用了低通滤波器。生成的滤波残差取决于热和俘获状态，并为这些隐藏变量提供了所需的洞察力。然后，通过使用非线性拟合方法来最小化 (14) 式中所示的误差来找到时间常数。其中，k_th、k_Trap 和 C 是通过最小二乘法针对时间常数的每次尝试解来提取的。
$$\sum _n|G_{r,f}(n)-k_{th}{a}_{\text{Th}}(n)-k_{\text{Trap}}{a}_{\text{Trap}}(n)-C{|}^2.(14)$$
  (14) 式中，G_r,f 是前面提到的低通滤波残差信号。通常情况下，热模型和俘获模型产生的影响非常不同：热变化会导致整个信号范围内的变化较慢，而俘获则会导致主要与信号峰相关的较快变化。因此，我们发现可以将优化分成两个不同的问题：
  首先，通过优化以下内容来找到热时间常数：
$$\sum _n|G_{r,f}(n)-k_{\mathrm{th}}{a}_{\mathrm{th}}(n)-C_{\mathrm{th}}{|}^2(15)$$
  然后，从总残留物中减去热影响，从而最终通过优化以下内容来找到捕获时间常数：
$$\begin{array}{r}\sum _n|G_{r,f}^{\prime }(n)-k_{\text{Trap}}{a}_{\text{Trap}}(n)-C_{\text{Trap}}{|}^2\\ G_{r,f}^{\prime }(n)=G_{r,f}(n)-k_{\text{th}}^{\prime }{a}_{\text{th}}(n)-C_{\text{Th}}^{\prime }.(16)\end{array}$$
  在 (16) 式中，$k_{\mathrm{th}}^{\prime }$ 和 $C_{\mathrm{th}}^{\prime }$ 是使用最小二乘法针对最佳热时间常数提取的两个特定的常数。
  第二种使用两个优化问题的方案得到了广泛的认可，并提供了一些优势。首先，每个问题中优化变量的数量减少，加快了进程。其次，俘获模型和热模型具有相似的拓扑结构。事实上，当充电和放电时间常数非常接近时，俘获模型等于热模型。这个问题可能导致误差和优化问题中的局部最小值。