第一次参加数模国赛，太菜了~~~~意难平

问题一

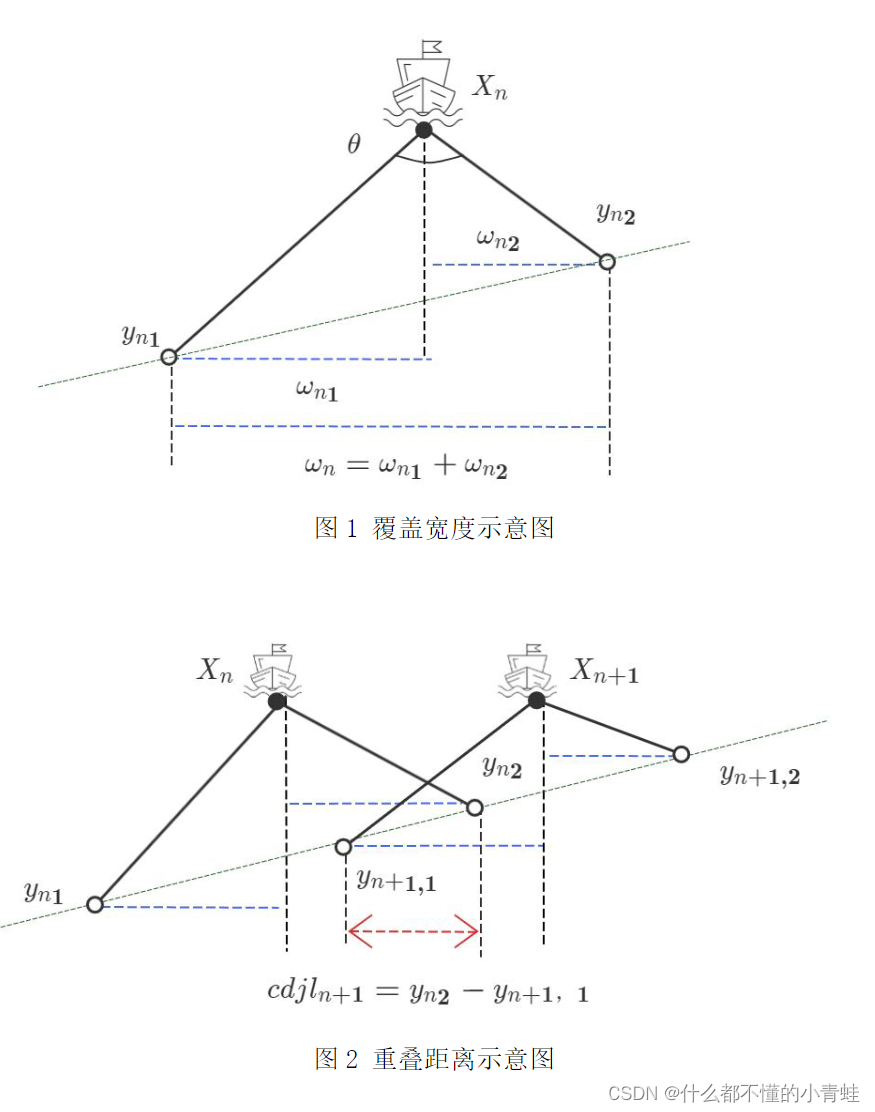
画出与测线方向垂直的平面和海底坡面的交线构成一条与水平面夹角为𝐀的斜线的情况下的示意图进行分析，将覆盖宽度分为左覆盖宽度和右覆盖宽度，求出它们与海水深度和𝐀、𝐀(复制的原因，没复制对，懒得改了)的关系。根据所列关系式，我们先计算出各个点位的海水深度，再求出覆盖宽度与重叠率，得出在 测线距中心点处的距离-600m 时的海水深度 为85.711553m，覆盖宽度为 297.3525571m，与前一条测线的重叠率为 33.639959%，具体计算结果如表 1 所示。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math
pi = math.pi
tan1_point5=math.tan(1.5/180*pi)
angle_degrees = 1.5
angle_radians = math.radians(angle_degrees)
tan_value = math.tan(angle_radians)##事先算出 tan1.5 的值
print("tan(1.5 degrees) =", tan_value)
angle_degrees1 = 60
angle_radians1 = math.radians(angle_degrees1)
tan_value1 = math.tan(angle_radians1)##事先算出 tan60 的值
m=200*tan_value
##分别求出海水深度然后合并
value=70
2
ans1=[]
for i in range(1,5):
ans1.append(value-i*m)
ans1.reverse()
ans1.append(70)
ans2=[]
for i in range(1,5):
ans2.append(value+i*m)
D=ans1+ans2
D.reverse()
##计算覆盖宽度 W
w1=[]
w2=[]
W=[]
for i in range(len(D)):
x1=(D[i]*tan_value1)/(1-tan_value1*tan_value)
x2=(D[i]*tan_value1)/(1+tan_value1*tan_value)
w1.append(x1)
w2.append(x2)
W.append(x1+x2)
print(w1)
print(w2)
print(W)
##计算重叠率
x=[-800,-600,-400,-200,0,200,400,600,800]
y1=[]
y2=[]
for i in range(len(W)):
y1.append(x[i]-w1[i])
y2.append(x[i]+w2[i])
print(y1)
print(y2)
chongdie=[]
for i in range(1,len(W)):
chongdie.append((y2[i-1]-y1[i])/(y2[i-1]-y1[i-1]))
print(chongdie)

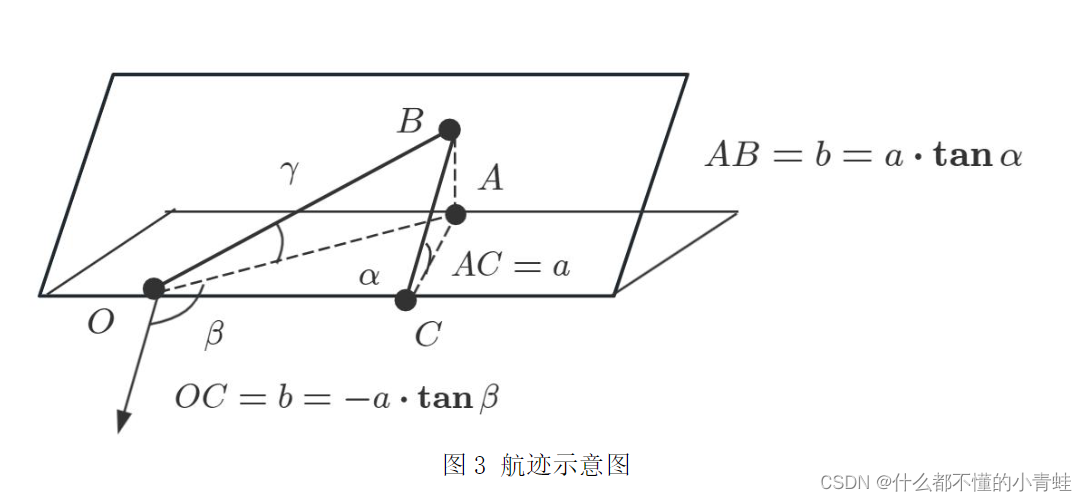
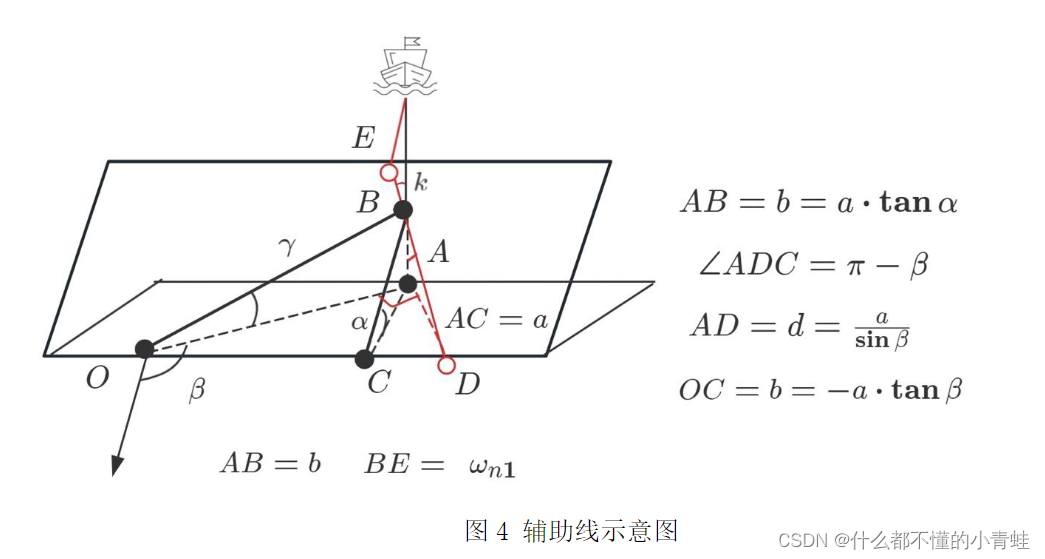
问题二

clc
clear
3
format long;%设置长小数格式
a=1.5/180*pi;
t=8;
D0=120;
theta=120/180*pi;
d=0.3*1852;%海里转化成米
for nbeta=1:1:t
beta=(nbeta-1)*pi*(360)/t*(t-1)/180/(t-1);
%检查 beta+pi/2 是否是 pi 的倍数
%如果 beta+pi/2 是 pi 的倍数，那么将 k1 设置为 0
%并将 k 设置为 a 的正切值的绝对值。
if mod(beta+pi/2,pi)==0;
k1=0;
k=abs(tan(a));
else
k=abs(tan(a)/sqrt(1+(tan(beta+pi/2))^2));
if 3*pi/2 > beta && pi/2 < beta;
k1=-tan(a)/sqrt(1+(tan(beta))^2);
else
k1=tan(a)/sqrt(1+(tan(beta))^2);
end
end
%深度计算
for n=1:1:t
x=(n-1)*d;
D(nbeta,n)=D0+x*k1;
end
%计算 w
for m=1:1:t
w1(nbeta,m)=D(nbeta,m)*sin(theta/2)/sin(pi/6-atan(k));
w2(nbeta,m)=D(nbeta,m)*sin(theta/2)/sin(pi/6+atan(k));
W(nbeta,m)=(w1(nbeta,m)+w2(nbeta,m))*cos(atan(k));
end
end

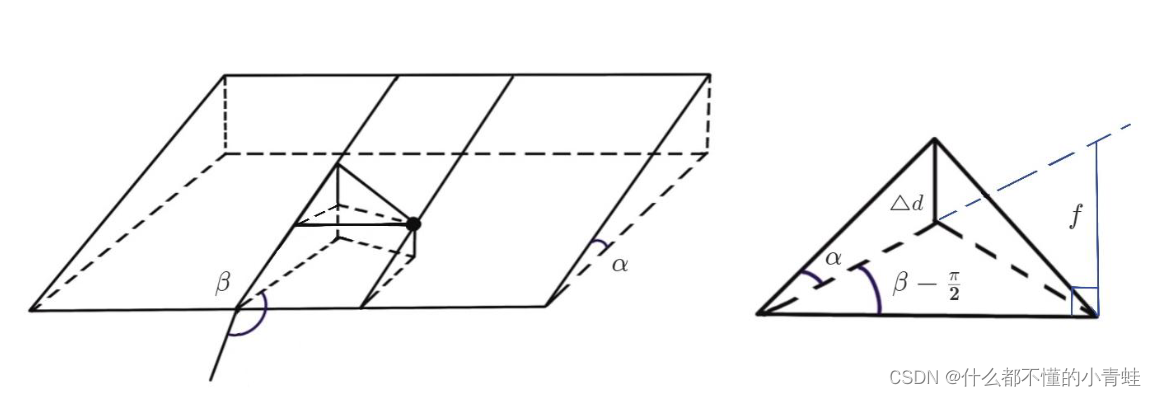
问题3

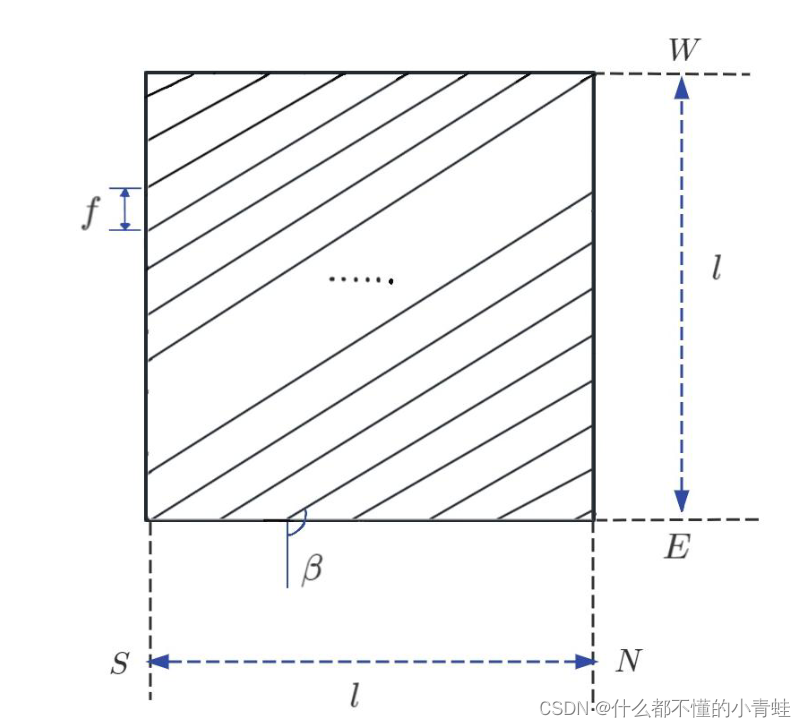
import numpy as np
import math
import geatpy as ea
class MyProblem(ea.Problem): 
def __init__(self):
4
name = 'MyProblem' 
M = 1 
maxormins = [1] 
-1：
Dim = 2 ）
varTypes = [0] * Dim 
lb = [math.pi/2, 0] 
ub = [ math.pi, 2*1852] 
lbin = [ 0, 0] 
ubin = [ 0, 0] 
# 调用父类构造方法完成实例化
ea.Problem.__init__(self,
name,
M,
maxormins,
Dim,
varTypes,
lb,
ub,
lbin,
ubin)
def evalVars(self, Vars): # 目标函数
beta= Vars[:, [0]]
f = Vars[:, [1]]
score = 4*1852*1852*2/(-np.cos(beta)*f)
#先把角度转化为弧度
angle_degrees_1 = 1.5
angle_radians_1 = math.radians(angle_degrees_1)
angle_degrees_60 = 60
angle_radians_60 = math.radians(angle_degrees_60)
k=np.arctan(1/(np.sin(beta)*np.tan(angle_radians_1)))
D=[]
for d in range(23,216):
D.append(abs(np.sin(k)*d*np.sin(angle_radians_60)/np.sin(k-angle_radians_60))+abs(np.sin(k)*(d+f*np.si
n(beta)*np.tan(angle_radians_1))*np.sin(angle_radians_60)/np.sin(k+angle_radians_60))
+f*np.cos(beta)-0.2*d*np.sin(angle_radians_60)*(abs(np.sin(k)/np.sin(k+angle_radians_60))+abs(np.sin(k
)/np.sin(k-angle_radians_60))))
D.append(0.1*d*np.sin(angle_radians_60)*(abs(np.sin(k)/np.sin(k+angle_radians_60))+abs(np.sin(k)/np.si
n(k-angle_radians_60))))
5
-abs(np.sin(k)*d*np.sin(angle_radians_60)/np.sin(k-angle_radians_60))+abs(np.sin(k)*(d+f*np.sin(beta)*n
p.tan(angle_radians_1))*np.sin(angle_radians_60)/np.sin(k+angle_radians_60))
+f*np.cos(beta)
CV=np.hstack(D)
return score, CV
if __name__ == '__main__':
# 实例化问题对象
problem = MyProblem()
# 构建算法
algorithm = ea.soea_DE_rand_1_bin_templet(
problem,
ea.Population(Encoding='RI', NIND=100),
MAXGEN=200, 
logTras=1) 
algorithm.mutOper.F = 0.5 
algorithm.recOper.XOVR = 0.7 
# 求解
res = ea.optimize(algorithm,
verbose=True,
drawing=1,
outputMsg=True,
drawLog=False,
saveFlag=True)
print(res)

问题4

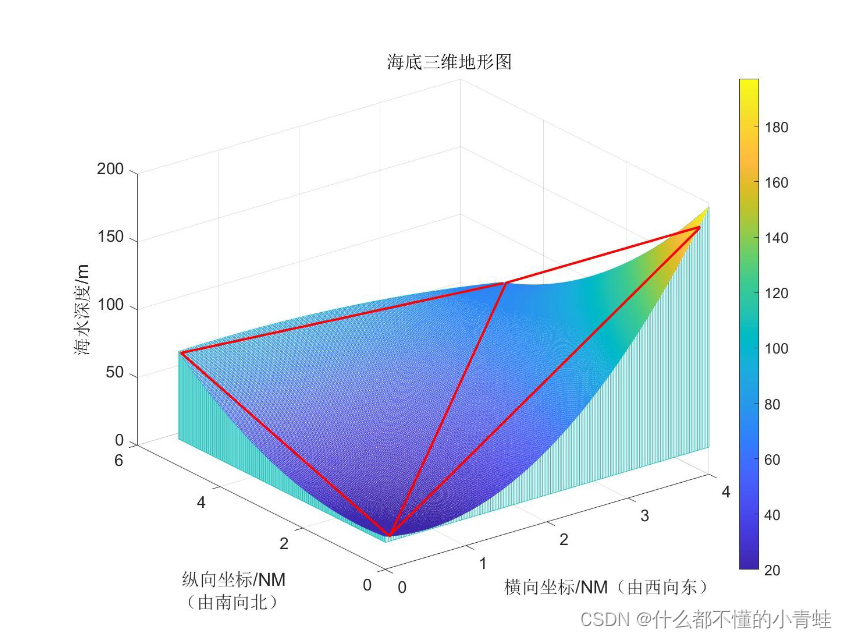
%读取数据
[X1,X2,X3]=xlsread("C:\Users\JJH\Desktop\CUMCM2023Problems\B 题\附件.xlsx");
x=X1(1,2:end);
y=X1(2:end,1);
z=X1(2:end,2:end);
cha=diff(z,1,2);
he=sum(cha(1,1:end));
average=he/250
[X Y]=meshgrid(x,y);
subplot(3,2,[1 2]);
meshz(X,Y,z);
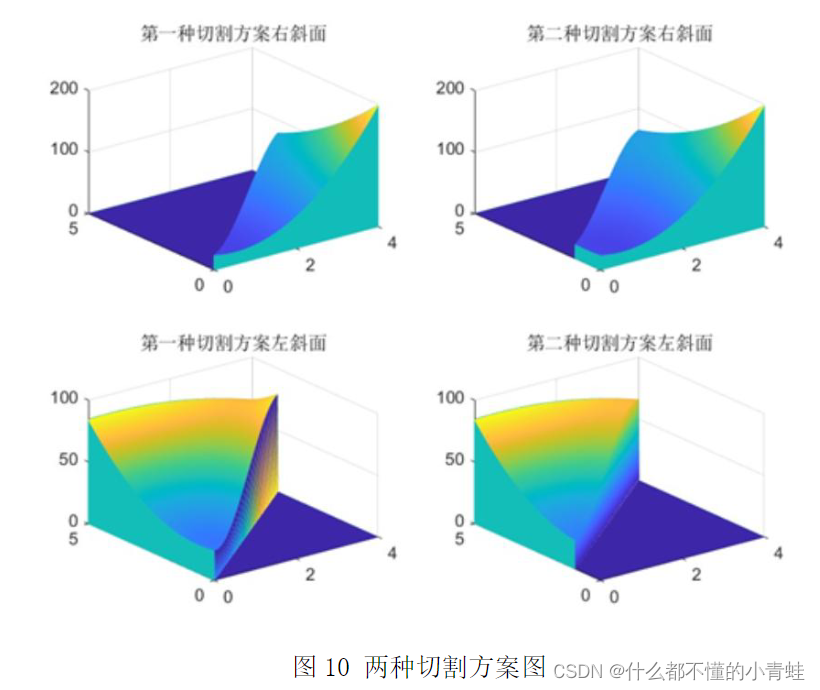
subplot(3,2,3);
z1=triu(z);
meshz(X,Y,z1)
6
subplot(3,2,4);
z2=triu(z,-50);
meshz(X,Y,z2)
subplot(3,2,5);
z3=tril(z);
meshz(X,Y,z3)
subplot(3,2,6);
z4=tril(z,-50);
meshz(X,Y,z4)
shading interp