目录
🦖解释 -- 树状数组
(一)公式
(二)操作
(1) 求前缀和
(2) 某个位置上的数更新
🦖解释 -- 线段树
🌼1264. 动态求连续区间和
AC 树状
AC 线段树
🌼1265. 数星星
暴力
AC 树状数组
🌼数列区间最大值(RMQ)
AC 线段树
AC DP
🌼小朋友排队
AC 树状
AC 归并
🦖解释 -- 树状数组
适用场景:前缀和 + 改变某个数字(注意与差分区别,差分是对一段区间加减;前缀和不能改变原数组)
(一)公式
树状数组C[x],x的二进制表示中,末尾有几个0就是第几层,比如10100,就是第2层,因为恰好 % 2^2 == 0
再举例,x的二进制表示,末尾有连续的 k 个 0,那么C[x]表示 区间 (x - 2^k, x] 的和
这里的 2^k = lowbit(x),即 C[x] 表示区间 (x - lowbit(x), x] 的和
【位运算】深入理解并证明 lowbit 运算_lowbit证明-CSDN博客
lowbit 表示 “最低位的 1 及其后面的所有的 0” 的二进制表示的数
lowbit(x) =
int lowbit(int x)
{
return x & -x;
}比如 x == 12,二进制为 1100,k == 2,C[12] 即 区间 (8, 12] 的和
即 C[12] = A[9] + A[10] + A[11] + A[12],或者 C[6] = A[5] + A[6] ...
树状数组C第 0 层恰好整除 2^0,第 1 层恰好整除 2^1,第 n 层恰好整除 2^n
树状数组最核心的公式👇
(x - lowbit(x), x] 区间的和 --> C[x]
核心:利用lowbit函数来跳过已经统计过的元素,从而实现高效的查询和更新操作
(树状数组每一个数,存的都是原数组一段的和)
(二)操作
O(logn)
(1) 求前缀和
{
for (int i = x; i > 0; i -= lowbit(i)) {
res += C[i];
}
return res;
}(2) 某个位置上的数更新
/*
A[x] + v
*/
for (int i = x; i <= n; i += lowbit(i))
C[i] += v; 举个例子,由图,当你更新7,只会影响到8,16...👇
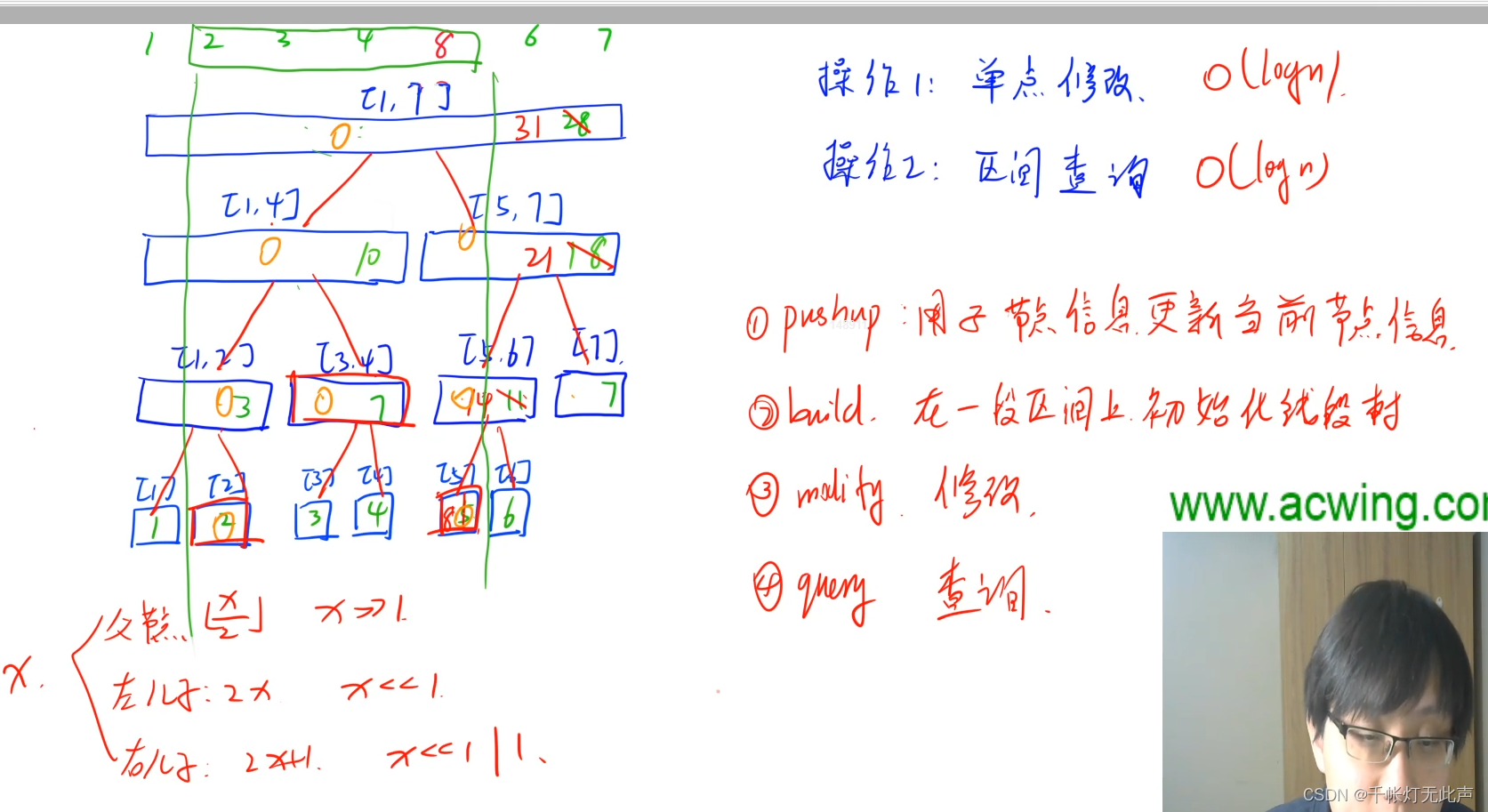
🦖解释 -- 线段树
线段树 - OI Wiki (oi-wiki.org)
AcWing 1264. 动态求连续区间和(⭐树状数组与线段树模板)(详细笔记) - AcWing
(Oi-wiki 看至区间修改和区间查询)
🌼1264. 动态求连续区间和
(动态区间求和一般用树状数组)
1264. 动态求连续区间和 - AcWing题库
树状数组模板题,3个函数,最好记忆下
AC 树状
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 100010;
int a[N], tr[N], n, m; // tr--tree
int lowbit(int x)
{
return x & -x;
}
void add(int x, int y) // 第 x 个元素加 y
{ // lowbit(i)而不是填x
for (int i = x; i <= n; i += lowbit(i)) // 这里是 +=
tr[i] += y;
}
int query(int x) //1~x 前缀和
{
int res = 0; // lowbit(i)而不是x
for (int i = x; i > 0; i -= lowbit(i)) // 这里是 -=
res += tr[i];
return res;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]); // 树状下标1开始
for (int i = 1; i <= n; ++i) add(i, a[i]); // 树状初始化
int k, x, y;
while (m--) {
scanf("%d%d%d", &k, &x, &y);
if (k == 0) printf("%d\n", query(y) - query(x - 1)); // 前缀和公式
else add(x, y);
}
return 0;
}AC 线段树
解释
(1)tr[]开 4*N,可能和倒数第2行的极端情况有关,比如1个,2个,1个,2个...元素交替
(2)query查询,build初始化,modify修改,当前编号都从1开始,也就是根节点开始,为了保证能遍历到需要的元素
(3)u << 1表示 u * 2,u << 1 | 1表示 u * 2 + 1
为什么此时 | 1 表示 + 1 呢,因为二进制中左移1后,右边最低位肯定为0,此时 | 1,0 | 1 == 1,相当于 + 1
(4)关于 query() 查询函数的第一个 if
if(l<=tr[u].l&&tr[u].r<=r)return tr[u].sum;最好结合Oi-wiki或者acwing,图的过程,认真分析一遍
因为它会不停左右递归,如果满足当前节点区间,被查询区间完全包含,就 += 当前节点的值(查询区间,可能由多个“当前”区间一段一段地组合成)
(5)关于 build() 开始的赋初值
// 记得赋值结构体初值, 即l, r tr[u] = {l, r};结构体
node的成员sum表示当前节点表示的区间的和。在函数build中,当递归到叶子节点时,我们直接将叶子节点的值设为w[l],即输入数组中对应位置的值。而对于非叶子节点,我们只需要赋值左边界l和右边界r,而不需要赋初值0给sum。这是因为在构建线段树的过程中,我们会通过递归不断地将子节点的信息更新到父节点,最终得到整个区间的和。在递归的过程中,如果当前节点是叶子节点,那么它的和就是
w[l],而对于非叶子节点,它的和是由左右子节点的和计算得到的。因此,在构建线段树的过程中,我们只需要关注区间的边界信息,而不需要关注和的初值。所以,在赋值结构体初值时,只需要赋值左边界
l和右边界r即可,而sum的初值会在后续的递归过程中根据子节点的和进行更新
坑
(1)build() 如果不是叶子节点后的else,需要先给结构体 tr[] 赋初值
(2)代码中的 mid,是当前节点的 mid,而不是查询区间的 mid
mid = tr[u].l + tr[u].r >> 1; 才对
代码
/*
线段树
pushup 子节点信息更新当前节点信息
build 在一段区间初始化线段树
modify 单点修改
query 区间查询
*/
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 100010;
int n, m, w[N]; // w[]输入的整数
// l当前节点左边界, r当前有边界
struct node {
int l, r, sum; // sum当前节点区间和
}tr[4 * N];
// 根据左右儿子计算父节点的值
void pushup(int u)
{
tr[u].sum = tr[u<<1].sum + tr[u<<1 | 1].sum;
}
// 初始化线段树, u当前编号, l左边界, r右边界
void build(int u, int l, int r)
{
if (l == r) tr[u] = {l, r, w[l]}; // 叶子节点直接赋值
// 分治递归
else {
// 记得赋值结构体初值, 即l, r
tr[u] = {l, r};
int m = tr[u].l + tr[u].r >> 1;
build(u<<1, l, m), build(u<<1|1, m + 1, r); // 递归左右儿子
pushup(u); // 根据左右儿子更新当前节点
}
}
// u当前编号, x节点 + v
void modify(int u, int x, int v)
{
if (tr[u].l == tr[u].r) tr[u].sum += v; // 叶节点, 直接modify
// 递归左右, 直到叶节点
else {
int m = tr[u].l + tr[u].r >> 1;
if (x <= m)
modify(u<<1, x, v); // 左边找左儿子
else
modify(u<<1|1, x, v); // 右边找右儿子
pushup(u); // 根据儿子更新当前节点
}
}
// 当前u, 计算 区间 [l, r] 的和
int query(int u, int l, int r)
{
if (l <= tr[u].l && r >= tr[u].r) // 当前区间在查询区间范围内
return tr[u].sum;
// 计算中间节点, 以便确定和查询区间交集情况
int m = tr[u].l + tr[u].r >> 1;
int sum = 0; // 当前总和
// 左边有交集
if (l <= m) sum += query(u<<1, l, r); // m为左边的右边界
// 右边有交集
if (r >= m + 1) sum += query(u<<1|1, l, r); // m+1 为右边左边界
return sum;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
build(1, 1, n); // 初始化线段树
int k, a, b;
while (m--) {
scanf("%d%d%d", &k, &a, &b);
if (k) modify(1, a, b);
else printf("%d\n", query(1, a, b));
}
return 0;
}🌼1265. 数星星
1265. 数星星 - AcWing题库
标签:中等,树状数组
暴力
AC 4/10 复杂度 O(n^2)
我觉得任何题,先模拟一遍,再想暴力做法,暴力想通了,最后才是通过数据结构,去优化(如果连暴力都不会,罔论优化)
/*
暴力 O(n^2)
y输入严格递增(y没用)
逆序遍历x,统计<=当前x的数量
*/
#include<iostream>
using namespace std;
const int N = 15010;
int a[N], ans[N]; //a[]记录x值
int main()
{
int n, y;
cin>>n;
for (int i = 0; i < n; ++i)
cin >> a[i] >> y;
for (int i = n - 1; i >= 0; --i) {
int num = 0; // num表示等级
for (int j = i - 1; j >= 0; --j) {
if (a[i] >= a[j]) num++; // <=当前x的数量
}
ans[num]++; // 该等级数量+1
}
for (int i = 0; i <= n - 1; ++i)
cout<<ans[i]<<endl;
return 0;
}AC 树状数组
树状数组每次+1 OR 前缀和,O(logn)
n个元素,O(n)
时间复杂度 O(nlogn)
树状数组,说白了就是动态前缀和....
坑:坐标x的范围和 n 无关,和 N 有关
/*
(有当前的前提条件,保证当前 y >= 前面的所有)
实际求的是 当前 1~x 有多少颗星星
a[x] 表示横坐标为 x 的星星数量
转化为求 当前 a[1] ~ a[x]的前缀和(x自增1)
每读入一个星星,a[x]++,对应tr[x]的 add()
两种操作:
(1)a[x]++
(2)a[]的前缀和
*/
#include<iostream>
using namespace std;
const int N = 32010;
int n, tr[N], ans[N >> 1]; // tr -- tree
int lowbit(int x)
{
return x & -x;
}
void add(int x, int y)
{
for (int i = x; i <= N; i += lowbit(i)) // i <= N而不是n, 范围是根据横坐标的
tr[i] += y;
}
int query(int x)
{
int res = 0;
for (int i = x; i > 0; i -= lowbit(i))
res += tr[i];
return res;
}
int main()
{
cin >> n;
int x, y;
for (int i = 0; i < n; ++i) {
cin >> x >> y;
x++; // 下标1开始
ans[query(x)]++; // 该等级星星数 + 1
add(x, 1);
}
for (int i = 0; i < n; ++i)
cout<<ans[i]<<endl;
return 0;
}🌼数列区间最大值(RMQ)
1270. 数列区间最大值 - AcWing题库
经典RMQ问题(Range Minimum Query 或 Range Maximum Query)(区间最小查询)
三种解决方法:线段树,树状数组,ST表(跳表)
本题由于查询次数 m <= 1e6,数列长度 n <= 1e5,如果限制时间 1s,会超时
(线段树比树状数组慢很多,尤其是数据量大的时候)
本题属于静态区间查询,所以线段树模板中的 4 个函数:pushup(),modify(),build(),query(),只需要 build() 和 query()
AC 线段树
坑
坑挺多的
(1)最小 int 最好取 INT_MIN,头文件 #include<bits/stdc++.h> 或者 #include<climits>
(2)注意 l, r 以及 tr[u].l, tr[u].r 的使用时机,build() 里可以用 l, r,其他的都用 tr[u].
(3)query() 最后记得 return Max
AC 代码
#include<iostream>
#include<cmath>
#include<cstdio>
//#include<bits/stdc++.h>
#include<climits> // INT_MIN
using namespace std;
const int N = 100010;
struct node {
int l, r, maxv;
}tr[N*4];
int n, m, w[N];
// u当前编号, l左边界编号, r右边界编号
void build(int u, int l, int r)
{
// 这里直接是 l, r 而非结构体的成员
if (l == r) // 叶节点直接赋值
tr[u] = {l, r, w[l]};
else {
// 先初始化
tr[u] = {l, r};
// 当前区间中点
int m = l + r >> 1;
// 递归左右儿子
build(u<<1, l, m), build(u<<1|1, m + 1, r);
// 向上更新最大值(根据左右儿子更新当前节点)
tr[u].maxv = max(tr[u<<1].maxv, tr[u<<1|1].maxv);
}
}
// u当前编号, 查询区间[l, r]
int query(int u, int l, int r)
{
if (l <= tr[u].l && r >= tr[u].r) // 查询区间包含当前区间
return tr[u].maxv;
int m = tr[u].l + tr[u].r >> 1, Max = INT_MIN; // 记得用INT_MIN
if (l <= m) Max = query(u<<1, l, r); // 左边有交集, 递归左儿子
if (r >= m + 1) Max = max(query(u<<1|1, l, r), Max); // 右边有交集, 递归右儿子
return Max; // 记得return
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
scanf("%d", &w[i]);
build(1, 1, n);
int a, b;
while (m--) {
scanf("%d%d", &a, &b);
printf("%d\n", query(1, a, b));
}
return 0;
}AC DP
对比下时间,线段树3000ms,DP 1000ms
解释
解释看代码开头注释,或者看看腾讯云的👇
难点在于查询,怎么将二进制转换成[l, r]的区间,这里没有证明,只给结论
查询
此处需要转换一下,因为dp[i][j]中,j 表示区间长度为 2^j,而非 r - l 的区间
令 k = log2(r - l + 1),
区间最大值RMQ[l, r] = max( dp[l][k], dp[r - 2^k + 1][k] ) 👈需要记忆
注意
dp[][]声明时,不要dp[N][N],因为 二维那里,dp[i][j] 的 j 表示 2^j,2^10 == 1024,
2^17 >≈ 1e5,所以声明为 dp[N][18]即可
难点
dp[][] 数组初始化和预处理后,需要根据给定的区间 [a, b] 查询最大值
由于 dp[][] 含义是根据二进制来的,这里需要记忆公式
代码
/*
(1)含义
dp[i][j] 第 i 位开始--连续 2^j 个数--中的最大值
第二个数表示 2 的多少次方
(2)递推式
将区间 [i, i + 2^j - 1] 分成两部分
每部分长度都为 2^(j - 1), 所以都是dp[][j - 1]
第一部分区间, i ~ i + 2^(j - 1) - 1
第二部分区间, i + 2^(j - 1) ~ i + 2^j - 1
所以递推式,取两部分区间的最大值:
dp[i][j] = max( dp[i][j - 1], dp[i + 2^(j - 1)][j - 1] )
(3)初始化
遍历时从1开始,初始值为 dp[i][0] = w[i] 数字本身
(4)遍历顺序
(5)打表检查
*/
#include<iostream>
#include<cstdio>
#include<cmath> //max(), log2()
using namespace std;
const int N = 100010;
int n, m, w[N], dp[N][18]; // 2^10 == 1024, 2^7 == 128, 所以100010 < 2^17
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
scanf("%d", &w[i]);
// 初始化dp[][]
for (int i = 1; i <= n; ++i)
dp[i][0] = w[i]; // 第 i 个数开始,连续1个数,为本身
// 预处理dp
for (int j = 1; (1 << j) <= n; ++j) // 区间长度 2^j
for (int i = 1; i + (1 << j) - 1 <= n; ++i) // 直到区间末尾, 为第 n 个数
dp[i][j] = max( dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1] );
// 打表检查
// for (int i = 1; i <= n; ++i) {
// for (int j = 0; i + (1 << j) - 1 <= n; ++j)
// cout<<dp[i][j]<<" ";
// cout<<endl;
// }
// 查询
int l, r;
while (m--) {
scanf("%d%d", &l, &r);
int k = log2(r - l + 1);
int ans = max(dp[l][k], dp[r - (1 << k) + 1][k]); // 二进制转...需记忆
printf("%d\n", ans);
}
return 0;
}🌼小朋友排队
1215. 小朋友排队 - AcWing题库
标签:贪心,树状数组,归并排序,中等
AC 树状
暴力👇
实际上就是找每个数(前面的逆序数 + 后面的逆序数) = S,
S即这个数的交换次数
因为交换1次不高兴值 + 1,第2次 + 2,第3次交换 + 3,交换第 S 次,不高兴值 + S
所以,对每个数, ans += (1 + 2 + ... + S),即 ans += n*(n-1) / 2
1 + 2 + ... + S 的和,就是这个小朋友的不高兴值,然后求和即可
树状数组👇
每读入一个数,就放入树状数组
void add(int x,int y){
for(int i=x;i<N;i+=lowbit(i)) tr[i]+=y;
}
int main()
{
...
add(a[i],1);
...
}这里,树状数组存的是这个数(高度)出现的次数,结合树状数组原理理解
add(a[i], 1) 表示 第 a[i] 个数(即这个高度), 出现次数 + 1
AC 代码
acwing卡BUG了,调试在50000个数据那里,一直不对,结果提交就AC了.....
#include<iostream>
#include<cstdio>
#include<cstring> // memset()
using namespace std;
const int N = 1000010; // 高度
typedef long long LL;
int sum[N], a[N], tr[N], n; // sum[i],N第i个小朋友交换次数
int lowbit(int x)
{
return x & -x;
}
void add(int x, int y) // 第x个数 + y
{
for (int i = x; i < N; i += lowbit(i)) // 这里是 < N
tr[i] += y;
}
int query(int x) // a[i] + ... + a[x] 的前缀和, 即身高<=a[i]的数量
{
int res = 0;
for (int i = x; i >= 1; i -= lowbit(i))
res += tr[i];
return res;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
a[i]++; // tr[]下标1开始
}
// 统计这个数前比它大的数量
for (int i = 1; i <= n; ++i) { // 前往后统计
add(a[i], 1); // 该位置人数 + 1
sum[i] += query(N-1) - query(a[i]); // query(a[i]):身高<= a[i]的数量
} // query[N-1]当前已读入数字个数
memset(tr, 0, sizeof tr); // 因为两次统计顺序不同
// 统计这个数后比它小的数量
for (int i = n; i >= 1; --i) { // 因为要统计第i个数之后,所以从后往前
add(a[i], 1);
sum[i] += query(a[i] - 1); // 第i个数后, <= a[i] - 1的数
}
LL ans = 0;
for (int i = 1; i <= n; ++i)
ans += (LL)sum[i] * (sum[i] + 1) / 2; // 公式是 + 1; 记得转LL
cout << ans << endl;
return 0;
}AC 归并
本质只是统计左右逆序数的个数,然后求和,类似以前的归并求逆序对模板题👇
788. 逆序对的数量 - AcWing题库
前置1,归并原理👇
排序——归并排序(Merge sort)-CSDN博客
前置2,归并求逆序对👇
归并求逆序对 -- 代码👇
/*
-- 视频6:20~11:00 多听几遍就懂了, 同时结合博客和题解
(1)
一个区间逆序对的数量 =
左边逆序对数量 + 右边 + 跨边界
具体可以: 5 1 2 3 7 6 4 (自己模拟下)
(2)
难点在于理解, 归并排序的详细过程
*/
#include<iostream>
#include<cstdio>
using namespace std;
typedef long long LL;
const int N = 100010;
int a[N], tmp[N];
LL ans; // 注意long long
void merge_Sort(int l, int r, int q[])
{
if (l >= r) return; // 分到只有一个元素, 递归出口
// 先递归 -- 分
int mid = (l + r) >> 1;
merge_Sort(l, mid, q), merge_Sort(mid + 1, r, q); // 递归左右
// 再合并 -- 治
int k = 0, i = l, j = mid + 1; // k是tmp[]的下标
while (i <= mid && j <= r) { // 左右任一遍历完之前
if (q[i] <= q[j]) tmp[k++] = q[i++];
else {
tmp[k++] = q[j++];
ans += mid - i + 1; // 关键:就多了这一行代码
}
}
// 仅剩左右其一未放入tmp[]
while (i <= mid) tmp[k++] = q[i++];
while (j <= r) tmp[k++] = q[j++];
// 将当前归并排序后元素, 放回原数组对应位置
for (int i = l, j = 0; i <= r; ++i, ++j)
q[i] = tmp[j];
}
int main()
{
int n;
scanf("%d", &n);
for (int i = 0; i < n; ++i)
scanf("%d", &a[i]);
merge_Sort(0, n - 1, a);
printf("%lld", ans); // 注意lld
return 0;
}本题解释 + 代码👇
解释
对照博客里的图,再结合归并中 “分” 和 “治” 的两个过程,多想几次就能理解

为什么使用二元组呢,因为数组a[i]根据身高排序,而sum[i] 统计编号为 i 的小朋友交换的次数,如果都使用 i ,当 a[i] 排序后, 编号就乱了
AC 代码
但是还有最后一步不是很理解,代码第36行
while (j <= r) temp[k++] = a[j++];为什么不需要 += mid - i + 1呢,先不想了,放个别人AC的代码,以后再遇到归并或者分治的题,再回来思考下
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
int n;
PII a[N]; //a[i]={身高,编号}
LL cnt[N]; //cnt[i]表示编号为i的小朋友交换次数
PII temp[N];
void merge(int l, int r)
{
if (l >= r) return;
int mid = l + r >> 1;
merge(l, mid), merge(mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (a[i] <= a[j])
{
//相对于i来说,j 前面的数都比它小, j 前面的数都和 i 交换过
cnt[a[i].y] += j - mid - 1;
temp[k++] = a[i++];
}
else {
//相对于j来说,i 后面的数都比它大, i 后面的数都和 j 交换
cnt[a[j].y] += mid - i + 1;
temp[k++] = a[j++];
}
while (i <= mid)
{
cnt[a[i].y] += j - mid - 1;
temp[k++] = a[i++];
}
while (j <= r) temp[k++] = a[j++];
for (int i = l, j = 0; i <= r; i++, j++) a[i] = temp[j];
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++) scanf("%d", &a[i].x), a[i].y = i;
merge(0, n - 1);
LL res = 0;
for (int i = 0; i < n; i++) res += (1 + cnt[i]) * cnt[i] / 2;
cout << res;
}