JZ36 二叉搜索树与双向链表（牛客）

描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。如下图所示

数据范围：输入二叉树的节点数 0≤10000≤n≤1000，二叉树中每个节点的值 0≤10000≤val≤1000
要求：空间复杂度O(1)（即在原树上操作），时间复杂度O(n)

注意:

1.要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构

4.你不用输出双向链表，程序会根据你的返回值自动打印输出

输入描述：

二叉树的根节点

返回值描述：

双向链表的其中一个头节点。

示例1

输入：

{10,6,14,4,8,12,16}

复制返回值：

From left to right are:4,6,8,10,12,14,16;From right to left are:16,14,12,10,8,6,4;

复制说明：

输入题面图中二叉树，输出的时候将双向链表的头节点返回即可。     

示例2

输入：

{5,4,#,3,#,2,#,1}

复制返回值：

From left to right are:1,2,3,4,5;From right to left are:5,4,3,2,1;

复制说明：

                    5
                  /
                4
              /
            3
          /
        2
      /
    1
树的形状如上图      

知识点1：二叉树递归

递归是一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。因此递归过程，最重要的就是查看能不能讲原本的问题分解为更小的子问题，这是使用递归的关键。

而二叉树的递归，则是将某个节点的左子树、右子树看成一颗完整的树，那么对于子树的访问或者操作就是对于原树的访问或者操作的子问题，因此可以自我调用函数不断进入子树。

知识点2：二叉搜索树

二叉搜索树是一种特殊的二叉树，它的每个节点值大于它的左子节点，且大于全部左子树的节点值，小于它右子节点，且小于全部右子树的节点值。因此二叉搜索树一定程度上算是一种排序结构。

思路：

二叉搜索树最左端的元素一定最小，最右端的元素一定最大，符合“左中右”的特性，因此二叉搜索树的中序遍历就是一个递增序列，我们只要对它中序遍历就可以组装称为递增双向链表。

具体做法：

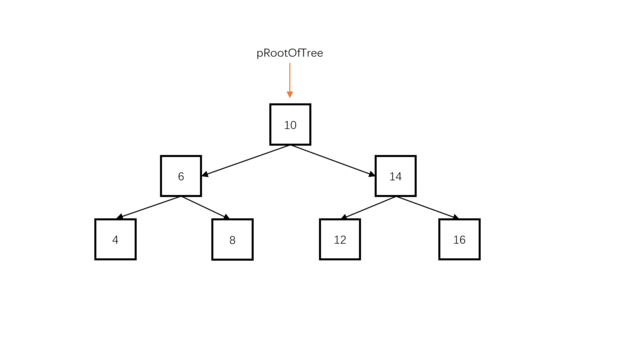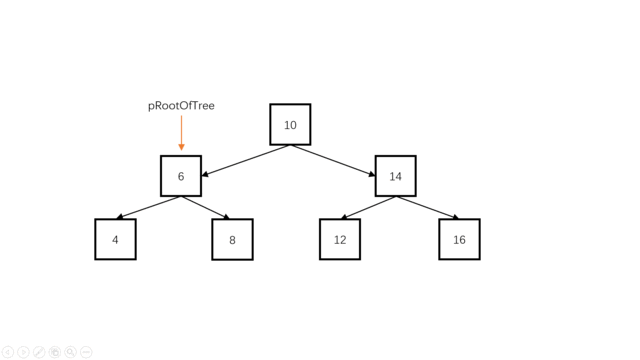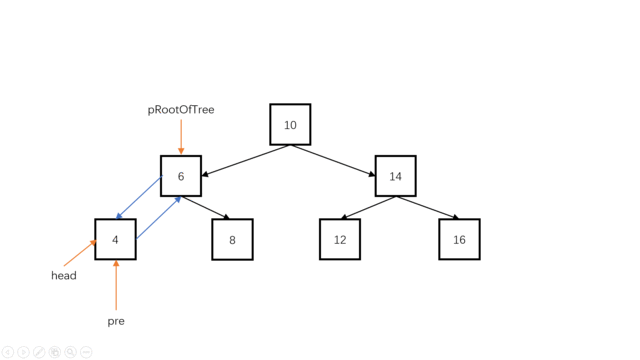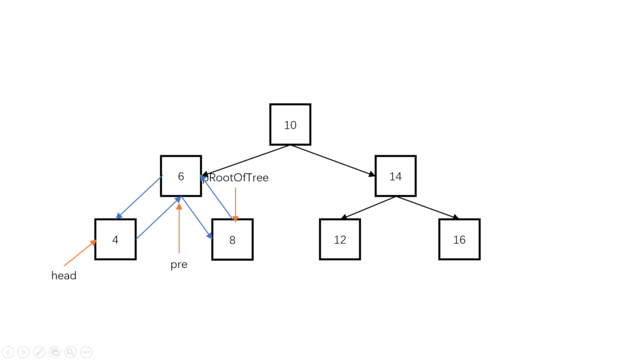
• step 1：创建两个指针，一个指向题目中要求的链表头（head），一个指向当前遍历的前一节点（pre)。
• step 2：首先递归到最左，初始化head与pre。
• step 3：然后处理中间根节点，依次连接pre与当前节点，连接后更新pre为当前节点。
• step 4：最后递归进入右子树，继续处理。
• step 5：递归出口即是节点为空则返回。

举一反三：

BM34. 判断是不是二叉搜索树

BM37. 二叉搜索树的最近公共祖先

 

class Solution {
public:
	TreeNode* head=nullptr;
	TreeNode* pre=nullptr;
    TreeNode* Convert(TreeNode* pRootOfTree) {
        if(pRootOfTree==nullptr)
		{
			return nullptr;
		}
		Convert(pRootOfTree->left);
		if(pre==nullptr)
		{
			pre=pRootOfTree;
			head=pRootOfTree;
		}
		else {
			pre->right=pRootOfTree;
			pRootOfTree->left=pre;
			pre=pRootOfTree;
		}
		Convert(pRootOfTree->right);
		return head;
    }
};