回归问题，例如之前做房子价格预测的线性回归问题

而softmax回归是一个分类问题,即给定一个图片，从猫狗两种动物类别中选出最可靠的那种答案，这个是两类分类问题，因为狗和猫是两类

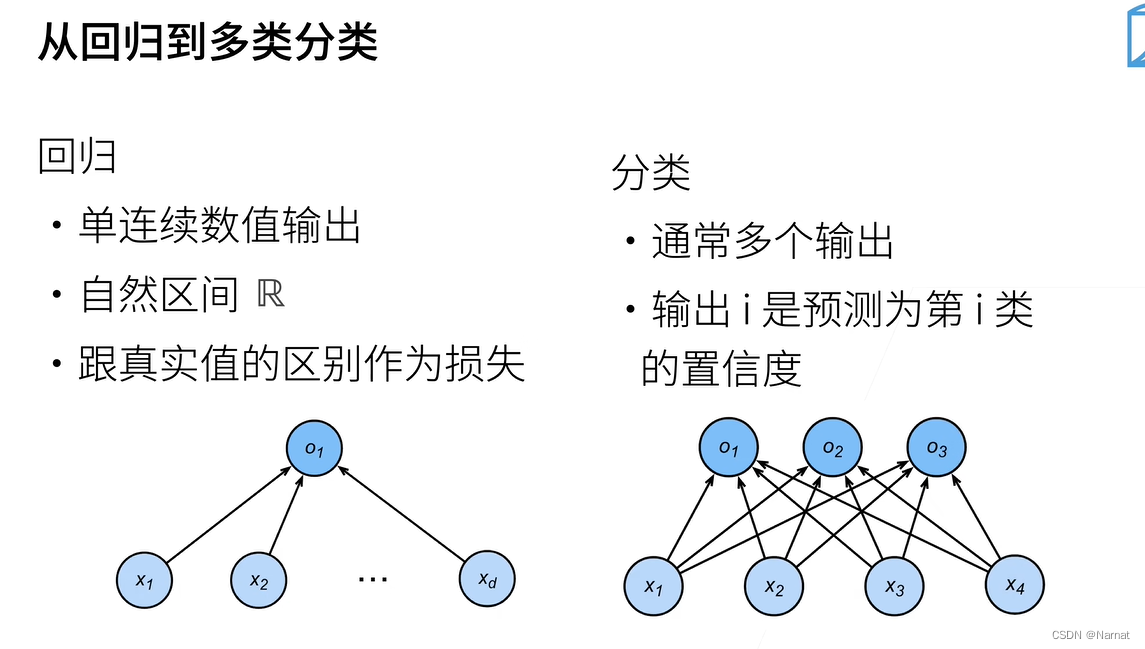
上述多个输出可以这样理解，假设一个图片让机器辨别这个图片的类别，假设是三类分类问题，分别是猫，狗，鸟，那么机器对图片分析假设会得出这样一个置信度的输出即[0.6, 0.3, 0.1]可以看出猫的置信度比较高为0.6，那么机器会判别这个图片为猫

继续拿上述猫狗鸟进行举例，那么y(注意这里不是小写y)可以是 [猫, 狗, 鸟]

假设上述让机器检测的图片就是猫，那么y1 = 1，其他都是0

即[1, 0, 0]

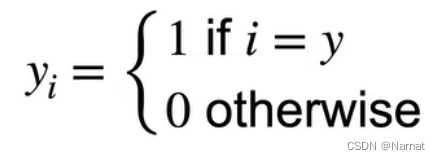
这其中的y就是被检测图片真实类别的标号

机器能对图片真实类别检测生成的置信度高于其他类别生成的置信度即可，朴素的来讲，只要机器识别这个图片是猫的概率比识别为其他动物的概率高即可

这里的exp是e的意思，即指数能化负数为正数，且这样算最后所有概率的和为1即上述0.6 + 0.3 + 0.1 =1

深度学习中log一般都是以e为底部

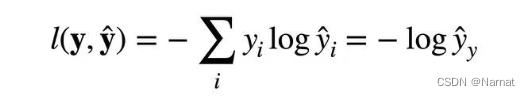
对上述求导得：

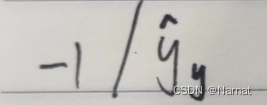
那为什么又说

以下是个人理解：

先弄明白yi是真实概率例如上述让识别图片是猫，那么真实是猫的概率为1，真实为狗，为鸟的概率为0而softmax(o)i就是预测概率

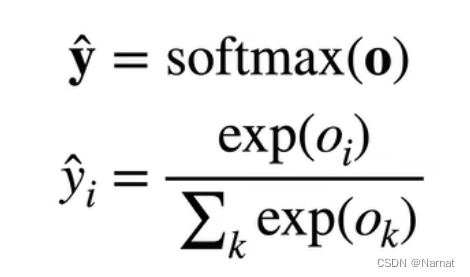
由上述这个等式可以化简出：

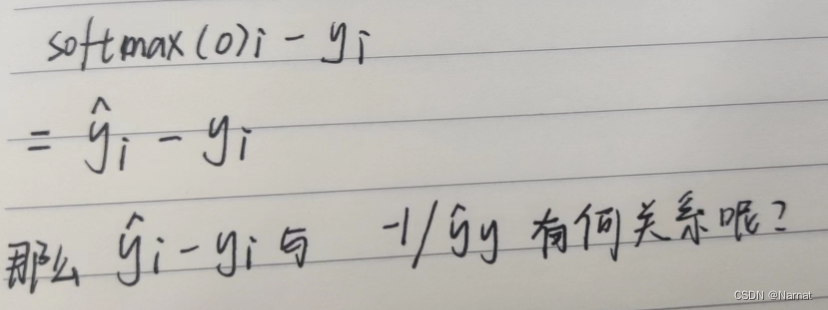
当i = y的时候两个式子可继续化简

可以看出当p越趋近1时p - 1越大，-1/p也越大

当p越趋近0时，p - 1越小，-1/p也越小

两个式子在变化趋势上是等效的。所以为什么说其梯度就是真实概率与预测概率的区别

这个纯属个人理解，需要实际案例去证实