[PyTorch][chapter 60][强化学习-2-有模型学习2]

news2024/11/28 3:44:55

前言：

前面我们讲了一下策略评估的原理,以及例子.

强化学习核心是找到最优的策略，这里

重点讲解两个知识点：

策略改进

策略迭代与值迭代

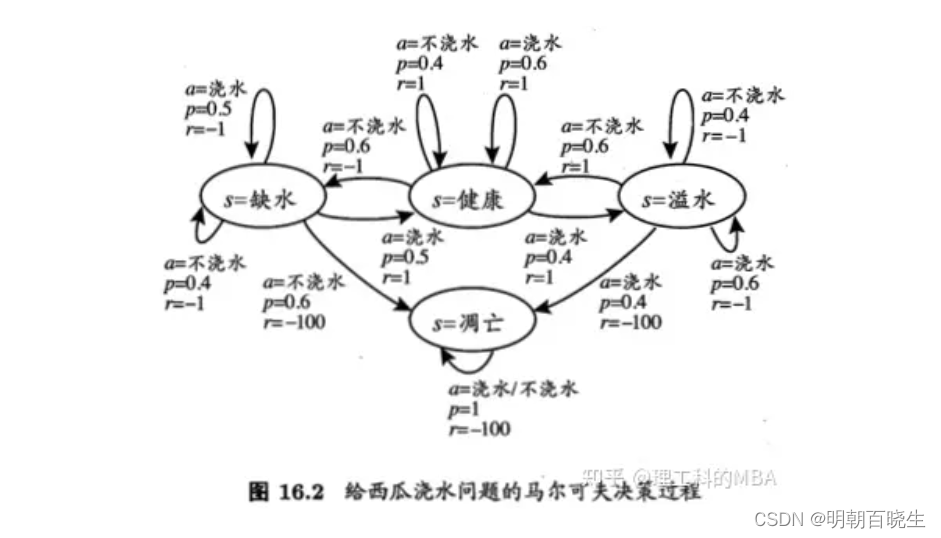
最后以下面环境E 为例，给出Python 代码

。

1：策略改进

2：策略迭代与值迭代

3：策略迭代代码实现 Python 代码

一策略改进

理想的策略应该能够最大化累积奖赏：

$\pi^{*}= arg max_{\pi} \sum_{x \in X} V^{\pi}(x)$

最优策略对应的值函数 $V^{*}$ 称为最优值函数

$\forall x\in X: V^{*}(x)= V^{\pi^*}(x)$

状态值函数（Bellman 等式）:

动作求和

$V_{T}^{\pi}=\sum_{a \in A}\pi(x,a)\sum_{x^{'}\in X}P_{x\rightarrow x^{'}}^a(\frac{1}{T}R_{x \rightarrow x^{'}}^a+\frac{T-1}{T}V_{T-1}^{\pi}(x^{'}))$ ......16.9

$V_{\gamma}^{\pi}=\sum_{a \in A}\pi(x,a)\sum_{x^{'}\in X}P_{x\rightarrow x^{'}}^a(R_{x \rightarrow x^{'}}^a+\gamma V_{\gamma}^{\pi}(x^{'}))$ ......16.9

状态-动作值函数

状态值函数（Bellman 等式）: 动作求和

$Q_{T}^{\pi}(x,a)=\sum_{x^{'}\in X}P_{x\rightarrow x^{'}}^a(\frac{1}{T}R_{x \rightarrow x^{'}}^a+\frac{T-1}{T}V_{T-1}^{\pi}(x^{'}))$ ...16.10

$V_{\gamma}^{\pi}(x,a)=\sum_{x^{'}\in X}P_{x\rightarrow x^{'}}^a(R_{x \rightarrow x^{'}}^a+\gamma V_{\gamma}^{\pi}(x^{'}))$ ...16.10

由于最优值的累计奖赏已经最大，可以对前面的Bellman 等式做改动，

即使对动作求和改为取最优

最优

$V_{T}^{\pi}=max_{a \in A}\sum_{x^{'}\in X}P_{x\rightarrow x^{'}}^a(\frac{1}{T}R_{x \rightarrow x^{'}}^a+\frac{T-1}{T}V_{T-1}^{*}(x^{'}))$ ....16.13

$V_{\gamma}^{\pi}=\sum_{x^{'}\in X}P_{x\rightarrow x^{'}}^a(R_{x \rightarrow x^{'}}^a+\gamma V_{\gamma}^{*}(x^{'}))$ ...16.13

则 $V^{*}(x)=max_{a\in A}Q^{\pi^{*}}(x,a)$ ....16.14 带入16.10

$Q_{T}^{*}(x,a)=\sum_{x^{'}\in X}P_{x\rightarrow x^{'}}^a(\frac{1}{T}R_{x \rightarrow x^{'}}^a+\frac{T-1}{T}max_{a^{'} \in A}Q_{T-1}^{*}(x^{'},a^{'}))$ ...16.10

$V_{\gamma}^{\pi}(x,a)=\sum_{x^{'}\in X}P_{x\rightarrow x^{'}}^a(R_{x \rightarrow x^{'}}^a+\gamma max_{a^{'} \in A} Q_{\gamma}^{*}(x^{'},a^{'}))$ ...16.10

最优Bellman 等式揭示了非最优策略的改进方式：

将策略选择的动作改变为当前的最优动作。这样改进能使策略更好

策略为 $\pi^{'}$ ,改变动作的条件为： $Q^{\pi}(x,\pi^{'}(x)) \geq V^{\pi}(x)$

带入16.10,可以得到递推不等式

$V^{\pi}(x)\leq Q^{\pi}(x,\pi^{'}(x))$

$=\sum_{x^{'} \in X}P_{x\rightarrow x^{'}}^{\pi^{'}(x)}(R_{x\rightarrow x^{'}}^{\pi^{'}(x)}+\gamma V^{\pi}(x^{'}))$

$=\sum_{x^{'} \in X}P_{x\rightarrow x^{'}}^{\pi^{'}(x)}(R_{x\rightarrow x^{'}}^{\pi^{'}(x)}+\gamma Q^{\pi}(x^{'},\pi^{'}(x^{'})))$

$=V^{\pi^{*}}(x)$ 16.16

二策略迭代与值迭代

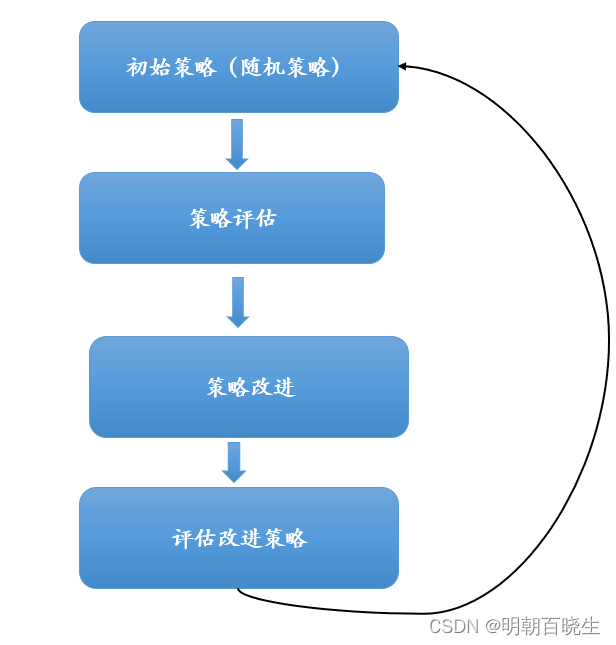
可以看出：策略迭代法在每次改进策略后都要对策略进行重新评估，因此比较耗时。

由公式16.16 $V^{\pi}(x)\leq Q^{\pi}(x,\pi^{'}(x))\leq V^{\pi^{*}}(x)$ 策略改进与值函数的改进是一致的

由公式16.13可得

$V_{T}(x)=max_{a \in A}\sum_{x^{'}\in X}P_{x\rightarrow x^{'}}^a(\frac{1}{T}R_{x \rightarrow x^{'}}^a+\frac{T-1}{T}V_{T-1}^{*}(x^{'}))$

$V_{\gamma}^{\pi}=max_{a\in A}\sum_{x^{'}\in X}P_{x\rightarrow x^{'}}^a(R_{x \rightarrow x^{'}}^a+\gamma V_{\gamma}^{*}(x^{'}))$

于是可得值迭代（value iteration）算法.

三策略迭代代码实现

# -*- coding: utf-8 -*-
"""
Created on Wed Nov  1 19:34:00 2023

@author: cxf
"""

# -*- coding: utf-8 -*-
"""
Created on Mon Oct 30 15:38:17 2023

@author: chengxf2
"""
import numpy as np
from enum import Enum
import copy



class State(Enum):
    #状态空间X    
    shortWater =1 #缺水
    health = 2   #健康
    overflow = 3 #凋亡
    apoptosis = 4 #溢水

class Action(Enum):
    
    #动作空间A
    water = 1 #浇水
    noWater = 2 #不浇水
    
class Env():
    
    def __init__(self):
        
        #状态空间
        self.X = [State.shortWater, State.health,State.overflow, State.apoptosis]   
        #动作空间
        self.A = [Action.water,Action.noWater]   
        
        #从状态x出发,执行动作a,转移到新的状态x'，得到的奖赏 r为已知道
        self.Q ={}
        self.Q[State.shortWater] =          [[Action.water,0.5,   State.shortWater,-1],
                                             [Action.water,0.5,   State.health,1],
                                             [Action.noWater,0.4, State.shortWater,-1],
                                             [Action.noWater,0.6, State.overflow,-100]]


        self.Q[State.health] =                [[Action.water,0.6,  State.health,1],
                                              [Action.water,0.4,   State.overflow,-1],
                                              [Action.noWater,0.6, State.shortWater,-1],
                                              [Action.noWater,0.4, State.health,1]]


        self.Q[State.overflow] =                [[Action.water,0.6,   State.overflow,-1],
                                                 [Action.water,0.4,   State.apoptosis,-100],
                                                 [Action.noWater,0.6, State.health,1],
                                                 [Action.noWater,0.4, State.overflow,-1]]


        self.Q[State.apoptosis] =[[Action.water,1, State.apoptosis,-100],
                                [Action.noWater,1, State.apoptosis,-100]]
        
        self.curV ={} #前面的累积奖赏,t时刻的累积奖赏
        self.V ={} #累积奖赏,t-1时刻的累积奖赏
        for x in self.X:    
             self.V[x] =0
             self.curV[x]=0
             
        
    def GetX(self):
        #获取状态空间
        return self.X

    def GetAction(self):
        #获取动作空间
        return self.A
    
    def GetQTabel(self):
        #获取状态转移概率
        return self.Q
    
    

class LearningAgent():
    
    def initStrategy(self):   
        #初始化策略
        stragegy ={}
        stragegy[State.shortWater] = Action.water
        stragegy[State.health] =    Action.water
        stragegy[State.overflow] = Action.water
        stragegy[State.apoptosis] = Action.water
        
        self.stragegy = stragegy
    
    def __init__(self):
          
          env = Env()
          self.X = env.GetX()
          self.A = env.GetAction()
          self.QTabel = env.GetQTabel()
          
          self.curV ={} #前面的累积奖赏
          self.V ={} #累积奖赏
          for x in self.X:    
              self.V[x] =0
              self.curV[x]=0
              
    def  evaluation(self,T):
         #策略评估
         
         for t in range(1,T):
             #当前策略下面的累积奖赏
             
             
             for  state in self.X: #状态空间
                     reward = 0.0
                     action = self.stragegy[state]
                     QTabel= self.QTabel[state]
                     
                     for Q in QTabel:
                         if action == Q[0]:#在状态x 下面执行了动作a,转移到了新的状态，得到的r
                             newstate = Q[2] 
                             p_a_ss =   Q[1]
                             r_a_ss =   Q[-1]
                             #print("\n p_a_ss",p_a_ss, "\t r_a_ss ",r_a_ss)
                             reward += p_a_ss*((1.0/t)*r_a_ss + (1.0-1/t)*self.V[newstate])
                             
                     self.curV[state] = reward               
             if (T+1)== t:
                 break
             else:
                 self.V = self.curV
         
              
         
     
     
    def  improve(self,T):
         #策略改进
         stragegy ={}
         for  state in self.X:
             
             QTabel= self.QTabel[state]
             max_reward = -float('inf') 
             
             #计算每种Q(state, action)
             for action in self.A:
                 
                     reward = 0.0
                     for Q in QTabel:
                         if action == Q[0]:#在状态x 下面执行了动作a,转移到了新的状态，得到的r
                             newstate = Q[2] 
                             p_a_ss =   Q[1]
                             r_a_ss =   Q[-1]
                             #print("\n p_a_ss",p_a_ss, "\t r_a_ss ",r_a_ss)
                             reward += p_a_ss*((1.0/T)*r_a_ss + (1.0-1/T)*self.V[newstate])
                             
                     if reward> max_reward:
                         max_reward = reward
                         stragegy[state] = action
                         #print("\n state ",state, "\t action ",action, "\t reward %4.2f"%reward)
         return stragegy
                     
                     
             
         
        


              
 
    
    def compare(self,dict1, dict2):
        #策略比较
        
        for key in dict1:
            if dict1[key] != dict2.get(key):
               return False
         
        return True
                     

    def learn(self,T):
        
        #随机初始化策略
        self.initStrategy()
     
        n = 0
        while True:
              self.evaluation(T-1) #策略评估
              n = n+1
         
              
             
                  
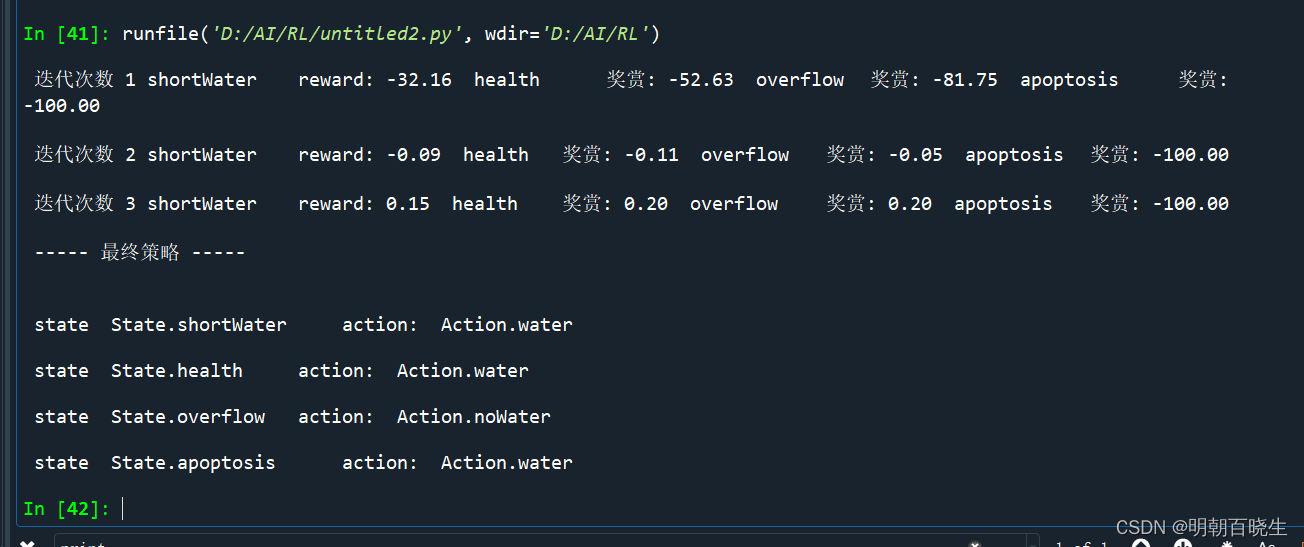
              print("\n 迭代次数 %d"%n ,State.shortWater.name, "\t 奖赏: %4.2f "%self.V[State.shortWater],
                    State.health.name, "\t 奖赏: %4.2f "%self.V[State.health],
                    State.overflow.name, "\t 奖赏: %4.2f "%self.V[State.overflow],
                    State.apoptosis.name, "\t 奖赏: %4.2f "%self.V[State.apoptosis],)
              
              
              
              strategyN =self.improve(T) #策略改进
              #print("\n ---cur---\n",self.stragegy,"\n ---new-- \n ",strategyN )
              if self.compare(self.stragegy,strategyN):
                  
               
                  print("\n ----- 最终策略 -----\n ")
                  
                  for state in self.X:
                      print("\n state ",state, "\t action: ",self.stragegy[state])
                  
                  break
              else:
                 
                  for state in self.X:
                      self.stragegy[state] = strategyN[state]
              
              
              

    
    



if __name__ == "__main__":
    T =10
    agent = LearningAgent()
    agent.learn(T)

参考：

机器学习.周志华《16 强化学习》_51CTO博客_机器学习周志华

CSDN

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1166626.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！