---

二叉树OJ进阶

---

一、 二叉树层序遍历

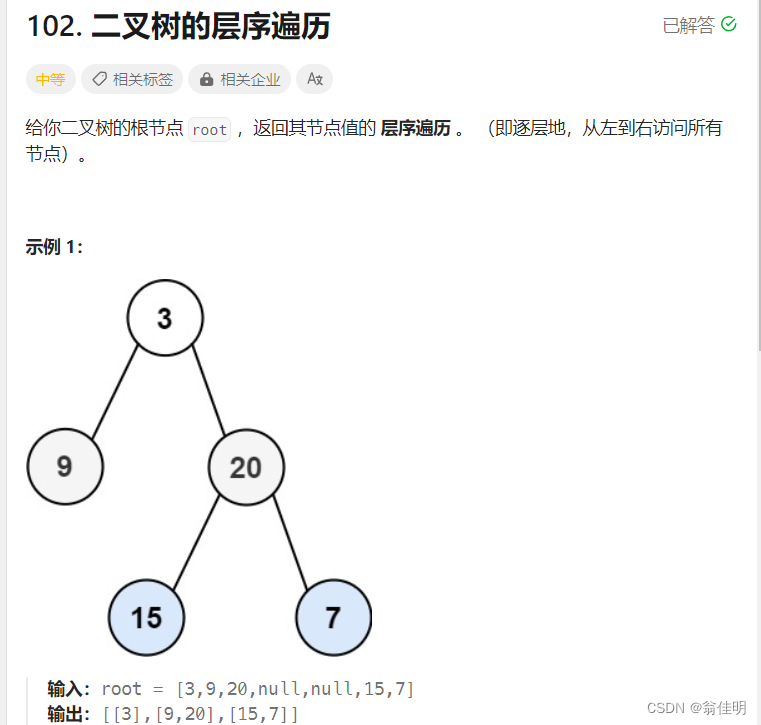
1.思路

用队列写：

1.从上到下，从左到右的顺序

2.非递归的方法：使用队列来完成

3.cur充当根结点，当cur不为空的时候，cur进入队列，队列不为空，cur弹出队列打印

4.如果cur的左边不为空，左边进队，右边不为空，右边进队

5.此时队列不为空，弹出队头（也就是cur的左边）打印，cur移动到cur的左边

6.也就是说，如果队列不为空，弹出一个队头元素并打印，弹出的元素的左右结点如果不为空，进队

7.先入再入右，保证从左到右打印，也就是说，利用队列先进先出（挤牙膏）的特性，先入队的是当前根结点的左右结点，然后是结点的左右结点，保证了从上到下打印，打印当前根结点的时候，根结点的左右结点进队

8.也就是说，在打印上层的每个结点时，每个结点的下一层元素按顺序进队，循环往复

9.当cur为叶子结点的时候，叶子结点的左右结点为空，不入队，只出队，当队列为空时，打印完毕

2.代码

    public List<List<Integer>> levelOrder2(TreeNode root) {
        List<List<Integer>> list = new ArrayList<>();
        if (root == null) {//根节点如果是0,返回空
            return list;
        }
        Queue<TreeNode> queue = new LinkedList<>();//实例化一个队列
        queue.offer(root);//根结点进队
        while (!queue.isEmpty()) {//队列不为空时
            int size = queue.size();
            List<Integer> tmp = new ArrayList<>();
            while (size != 0) {
                TreeNode cur = queue.poll();//取出之前进队的根节点，并让cur指向该结点
               // System.out.print(cur.val + " ");//取出来就打印
                tmp.add(cur.val);//取出来的值不打印，直接存进tmp
                size--;
                if (cur.left != null) {//该结点的左右子树如果不为空，进队
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
            list.add(tmp);
        }
        return list;
    }

二、根据二叉树创建字符串

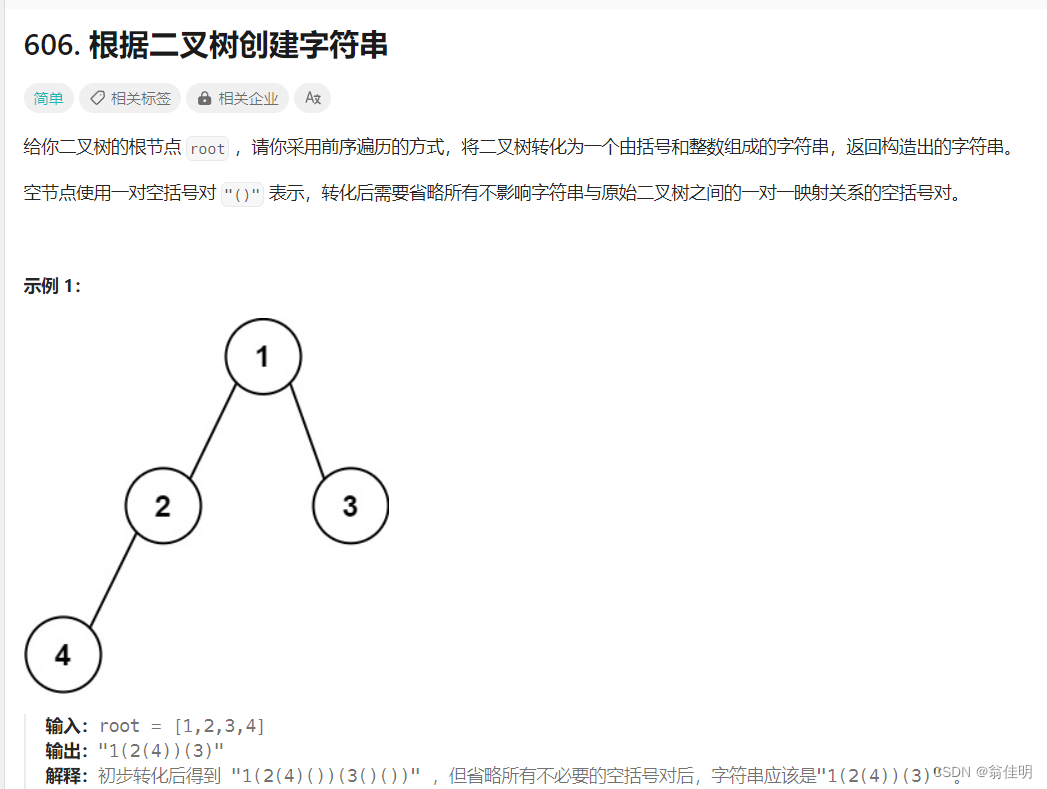
1.思路

1.前序遍历，用StringBuilder拼接字符串

2.放进根节点，如果子结点不为空 + “（ ”

3.左右子树如果都为空，直接返回

4.子树走完了，+ “ ）”

5.左边为空，右边不为空 + “（）”

• 也就是说，当结点的左子树不为空时，先拼接当前结点，然后+（ ，进入左子树的递归
• 当出现左子树为空，右子树不为空的情况时，+（）
• 左子树递归完了+），判断右子树，右子树为空返回，不为空，+（ ，进入右子树的递归

2.代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public String tree2str(TreeNode root) {
        if (root == null) {
            return null;
        }
        StringBuilder stringBuilder = new StringBuilder();
        tree2strChild(root, stringBuilder);
        return stringBuilder.toString();

    }

    public void tree2strChild(TreeNode root, StringBuilder sb ){
        if (root == null){//root等于空，直接返回
            return;
        }
        sb.append(root.val);//拼接root的值
        if (root.left!=null){//左边不为空的情况
            sb.append('(');
            tree2strChild(root.left,sb);//进入左子树判断
            sb.append(')');//左子树完成后+）
        }else {
            //左边为空
            if (root.right!=null){//左边为空，右边不为空
                sb.append("()");
            }else {
               return;//左右都为空，直接返回
            }
        }
        if (root.right!=null){//右边不为空的情况
            sb.append('(');
            tree2strChild(root.right,sb);
            sb.append(')');//右子树完成后+）
        }else {
            return;
        }
    }
}

三、判断完全二叉树

判断一棵树是不是完全二叉树

1.思路

1 .和层序遍历类型，用队列来完成

2 .如果根节点不为空，根节点入队

3.判断队列如果不为空，弹出队头并用cur引用（用cur指向该结点）

4.将cur的左有子结点进队，不论空不空

5.进入循环，队列不为空，弹出当前的头结点。cur的左右子节点进队（不管空不空）

6.当队列中弹出的元素为空的时候，cur指向空，所以结点都遍历完毕，循环结束

7.此时，当队列不为空时进行循环，依次取出队列中的元素，如果出现不为空的元素，说明不是完全二叉树

8.如果队列中都是空，说明是完全二叉树

• 因为完全二叉树就是从上到下，从左到右依次排列，队列中的元素按层序排序依次放加入
• 如果出现加杂着null的情况，证明不是完全二叉树

2.代码

    // 判断一棵树是不是完全二叉树
   public boolean isCompleteTree(TreeNode root){
        if (root == null){
            return true;
        }//尽量接口引用对象
       Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()){//队列不为空
            TreeNode cur = queue.poll();//弹出对队头
            if (cur != null){//cur不为空，左右子节点进队
                queue.offer(cur.left);
                queue.offer(cur.right);
            }else{
                break;//cur为空，结束循环
            }
        }
        while (!queue.isEmpty()){
            TreeNode tmp = queue.poll();//依次出队
            if (tmp != null){
                return false;
            }
        }
        return true;
   }

四、二叉树的构建及遍历

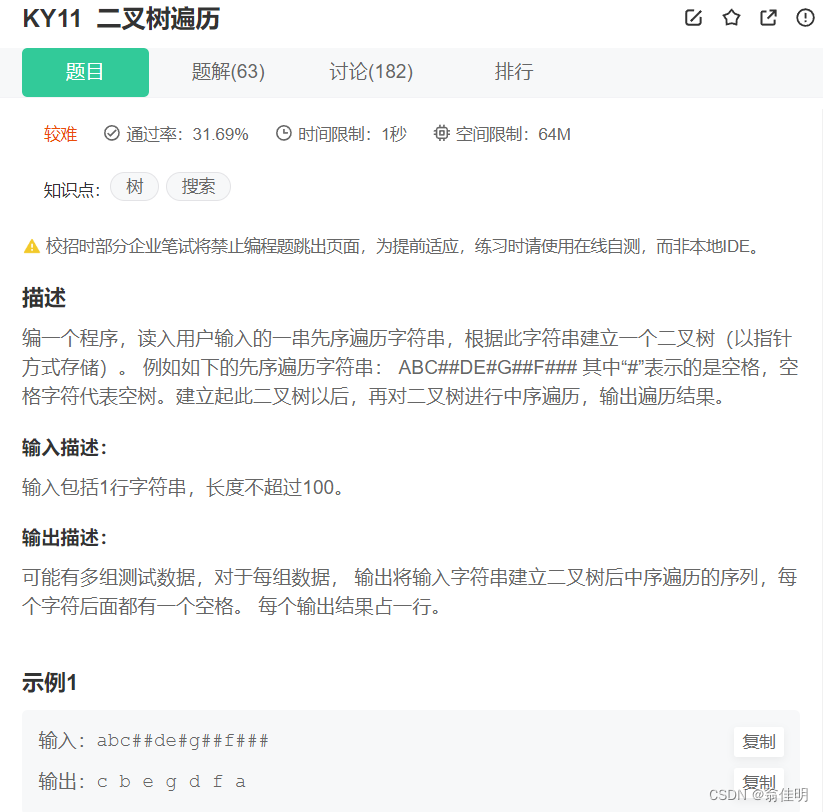
1.思路

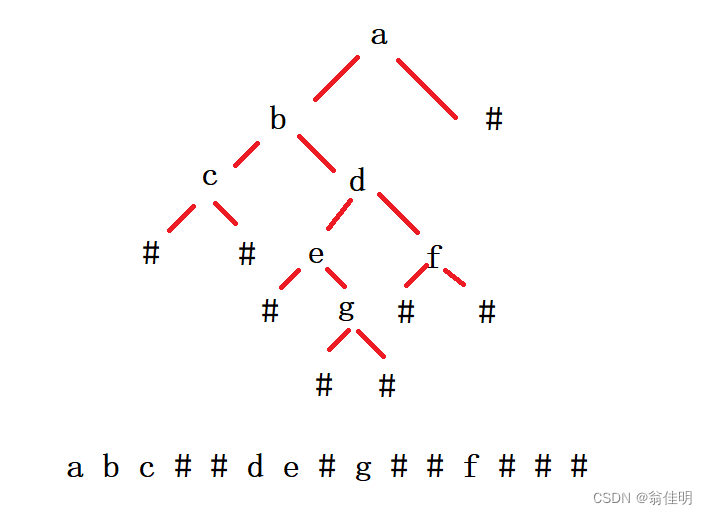
1.根据前序遍历的字符串，创建二叉树，再通过创建的二叉树，打印中序遍历

2.给了前序遍历，可以找到根节点的位置

3.#代表空树，空节点是指定的，因此可以创建唯一二叉树

4.前序遍历，先创建根节点，如果遇到#，返回的同时用子节点接收

5.因为要递归，所以不采用循环来遍历字符串，设置一个静态成员变量i

6.读取字符串中i位置的字符，如果不是#，根据取到的值创建根节点，i++;

7.先创建左子树，再创建右子树，根节点为空时返回，根节点的左右分别指向返回值

8.如果遇到#,i++，返回的结点为null

9.利用中序遍历打印

2.代码

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while (in.hasNextLine()) { // 
           String str = in.nextLine();
           TreeNode root = creatTree(str);
           inorder(root);
        }
    }
    public static int i = 0;//i记录读取的字符
    public static TreeNode creatTree(String str){//创建二叉树
        TreeNode root = null;
       if(str.charAt(i)!='#'){
        root = new TreeNode(str.charAt(i));
        i++;//创建完根节点后，i++,先创建左树，再创建右树
        root.left = creatTree(str);
        root.right = creatTree(str);
       }else{
        i++;//如果是#,i++跳过
       }
        return root;//返回root，i是#时，返回空，i不是#时，返回结点，让root指向对应结点
    }
    public static void inorder(TreeNode root){
        if(root==null){//中序遍历打印
            return;
        }
        inorder(root.left);
        System.out.print(root.val+" ");
        inorder(root.right);
    }
}

• i 会不会越界？
• 不会，递归的次数严格执行给的前序遍历，除非给的字符串非法，否则i不会越界

五、二叉树的最近公共祖先

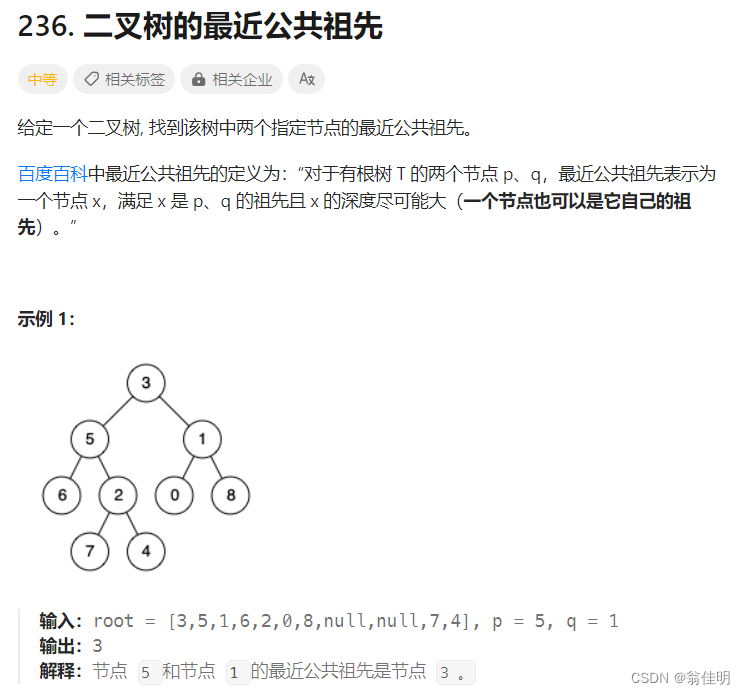
方法一：思路

方法一：

1.p、q可能在根的左右两边

2.要么都在根的左边或者右边

3.要么其中一个结点是公共祖先

4.先判断如果p、q是根节点,则根节点就是公共祖先

5.递归，分别在左右两边去找p、q

6.如果左右两边递归回来的值都不为空，说明两边都找到了，根结点就是公共祖先，返回根节点

7.因为pq一定在树中，如果左右返回的值，一个为空，一个不为空，说明找到的值就是pq的公共祖先

8.如果左右都为空，没找到，返回null

代码

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null ){//判断是否为空，返回空
            return null;
        }
        if(root == q || root == p){//判断根节点是不是公共祖先
            return root;
        }
        TreeNode leftRet = lowestCommonAncestor(root.left,p,q);//在根的左边找pq 
        TreeNode rightRet = lowestCommonAncestor(root.right,p,q);//在跟的右边找pq

        if(leftRet != null && rightRet != null){//左右都不空
            return root;//如果左右两个分别都找到了，根节点就是公共祖先
        }else if(leftRet != null){//左边不为空，右边为空
        //因为pq存在于树中，所以找到的结点就是pq的公共祖先
            return leftRet;
        }else if(rightRet != null){//右边不为空，左边为空
            return rightRet;
        }
        return null;//左右都为空，返回空
    }

方法二：思路

如果给每一个结点加一个父亲结点，每一个结点都有父亲结点的地址，就变成了求相交结点

也可以用栈来完成：

• 因为栈是先进后出的，没有父亲结点，用栈来存储路径的上一个结点

1.用两个栈来存从根节点到p和q的路径上遇到的左右结点

2.两个栈，判断栈的大小，谁多谁先弹出一个，然后再同时弹出

3.将弹出的结点进行比较，值不一样，不是公共祖先，如果弹出的两个一样，则返回找到的结点

4.栈出空了，没有公共祖先，返回null

• 怎么找到路径，存放进栈(如何确保，栈中存的就是p、q的正确路径)

  1.根不为空，直接压栈，判断根节点是不是要找到结点

  2.根节点不是，递归：从左边开始找，左边没找到，再去右边找

  2.左右两边都没找到要找的结点，弹出压进的结点，返回false

代码

    public boolean getPath(TreeNode root, TreeNode node, Deque<TreeNode> stack) {//
        if (root == null || node == null) {
            return false;
        }
        stack.push(root);//根节点压栈
        //放完后检查，
        if (root == node) {
            return true;
        }//根节点不是，从左边开始找
        boolean ret1 = getPath(root.left, node, stack);
        if (ret1 == true) {
            return true;
        }//左边没找到，再去右边找
        boolean ret2 = getPath(root.right, node, stack);
        if (ret2 == true) {
            return true;
        }
        stack.pop();//左右都没找到弹出压进的结点
        return false;
    }

    public TreeNode lowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) {
        //在两个栈当中，存好对应的路径
        Deque<TreeNode> stack1 = new ArrayDeque<>();
        getPath(root, p, stack1);
        Deque<TreeNode> stack2 = new ArrayDeque<>();
        getPath(root, q, stack2);

        //判断栈的大小
        int size1 = stack1.size();
        int size2 = stack2.size();
        if (size1 > size2) {
            int size = size1 - size2;
            while (size != 0) {
                stack1.pop();
                size--;
            }
        } else {
            int size = size2 - size1;
            while (size2 != 0) {
                stack2.pop();
                size--;
            }
        }//栈里面结点的个数一样了
        while (!stack1.isEmpty()&&!stack2.isEmpty()){
            //如果两个栈都不为空，看弹出的值一不一样
            if (stack1.peek()!=stack2.peek()){//不相等，弹出
                stack1.pop();
                stack2.pop();
            }else {
                return stack1.peek();

            }
        }
        return null;//栈出空了，没有公共祖先，返回空
    }

点击移步博客主页，欢迎光临~