[双指针] (四) LeetCode 18.四数之和
文章目录
- [双指针] (四) LeetCode 18.四数之和
- 题目解析
- 解题思路
- 代码实现
- 总结
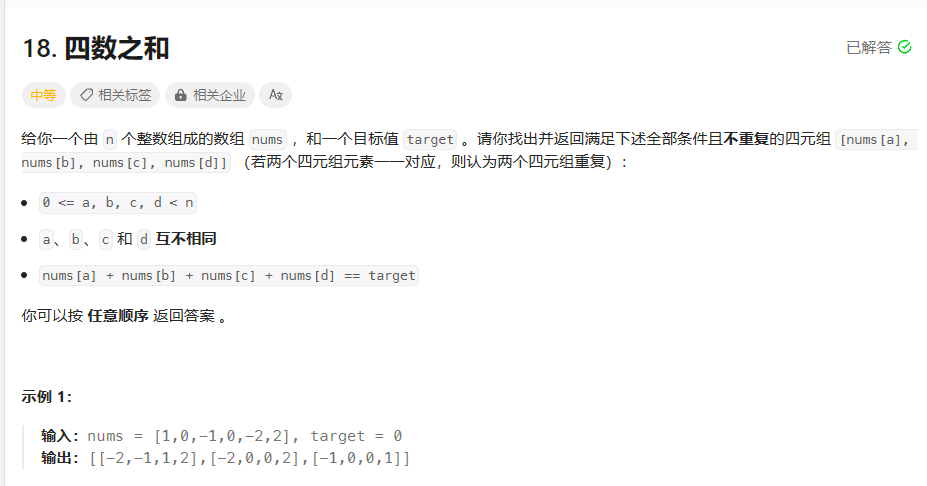
18. 四数之和
题目解析
(1) 从一个数组中找一个目标值target
(2) target = nums[a] + nums[b] + nums[c] + nums[d]
解题思路
和上一道题三数之和一样, 我们把四数之和 转换 为两数之和即可.
解法: 双指针
首先固定两个数, 再从余下的数中找出两个数即可.
如图中操作, 和 两数之和、三数之和操作类似,再多说也没有意义。

做过前两道题,理解图中思路和去重思路,可以实现代码后再来看下面的内容。
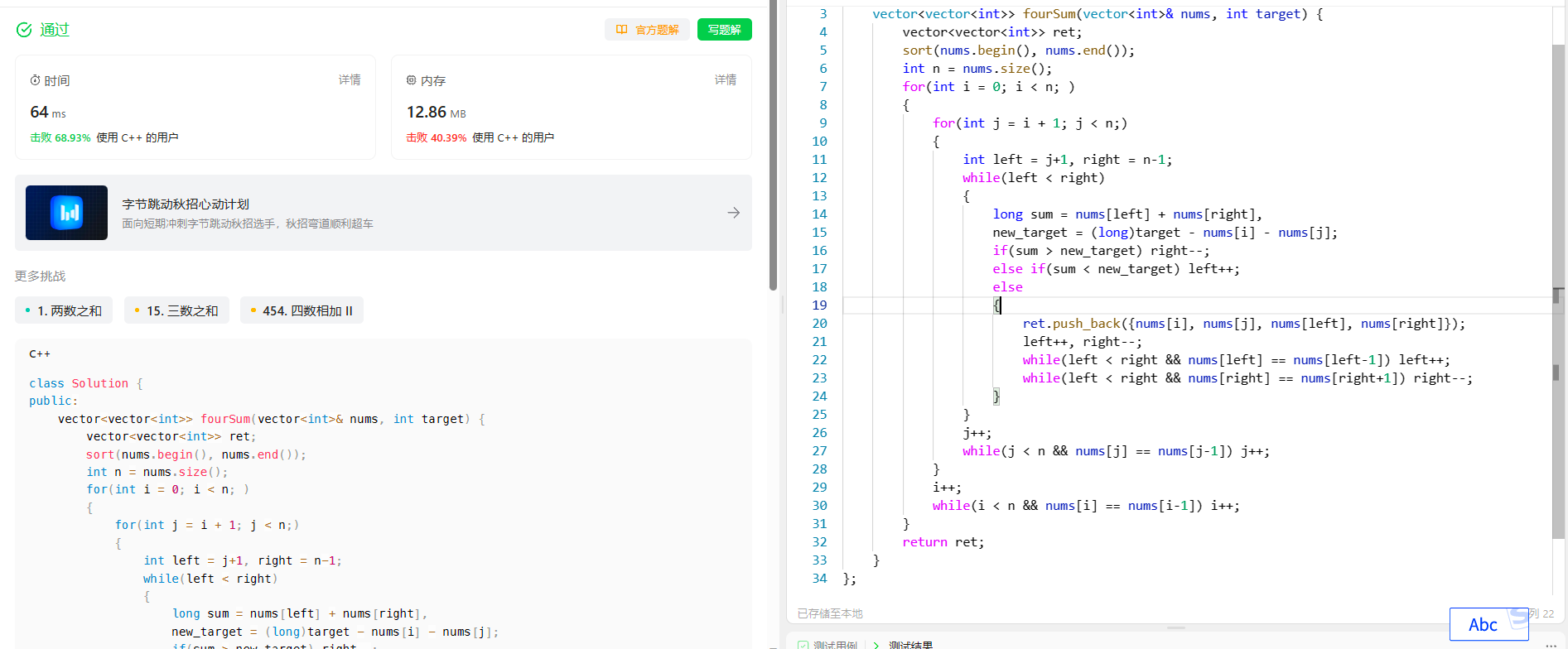
代码实现
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> ret;
sort(nums.begin(), nums.end());
int n = nums.size();
for(int i = 0; i < n; )
{
for(int j = i + 1; j < n;)
{
int left = j+1, right = n-1;
while(left < right)
{
long sum = nums[left] + nums[right],
new_target = (long)target - nums[i] - nums[j];
if(sum > new_target) right--;
else if(sum < new_target) left++;
else
{
ret.push_back({nums[i], nums[j], nums[left], nums[right]});
left++, right--;
while(left < right && nums[left] == nums[left-1]) left++;
while(left < right && nums[right] == nums[right+1]) right--;
}
}
j++;
while(j < n && nums[j] == nums[j-1]) j++;
}
i++;
while(i < n && nums[i] == nums[i-1]) i++;
}
return ret;
}
};
总结
细节1:四数之和即为多一个固定的数+三数之和
细节2:数据范围太大,即改定义long。
细节3:与三数之和相比,这里的target不是固定的,所以即使为正数也不必结束循环。
细节4:两个固定的数i,j都需要进行去重。