leetCode 198.打家劫舍动态规划入门:从记忆化搜索到递推

news2024/11/16 9:36:37

leetCode 198.打家劫舍 198. 打家劫舍 - 力扣（LeetCode）

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

「动态规划的核心」：状态定义和状态转移方程的思考方法，举“打家劫舍”为例，详细讲解如何通过回溯思路和子集型回溯思路来思考动态规划问题。同时，介绍如何优化回溯代码和使用递推思路来解决动态规划问题。

（一）状态定义？状态转移方程

启发思路：选或不选 / 选哪个

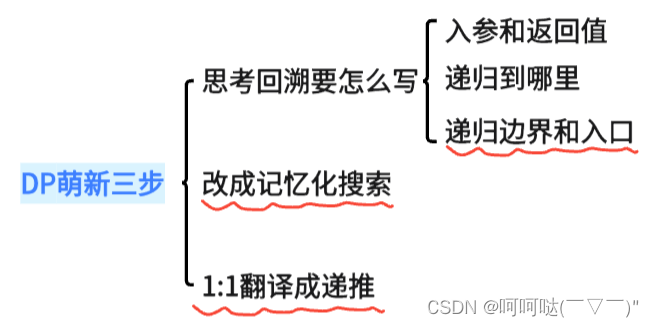
对于这个题，先把它看做是一道回溯题，要把一个大问题变成一个规模更小的子问题，从第一个房子或者最小一个房子开始思考，是最容易的，因为它们受到的约束是最小的。

比如考虑最后一个房子「选」还是「不选」，如果「不选」，那么问题就变成 $n-1$ 个房子的问题。如果选，问题就变成 $n-2$ 个房子的问题，不断这样去思考，就可以得到一棵搜索树了。

（二）回溯

由于在选的情况下，相邻的房子是不能选的，所以这里直接递归到 $n-2$ 个房子，把刚才的思考过程再抽象一下：当我们枚举到第 $i$ 个房子「选」或「不选」的时候，就确定了递归参数中的 $i$ ，那么 $dfs(i)$ 的含义是什么呢？就是从前 $i$ 个房子中得到的最大金额和。如果「不选」第 $i$ 个房子，问题就变成从 前 $i-1$ 个房子中得到的最大金额和。如果选第 $i$ 个房子，问题就变成从 前 $i-2$ 个房子中得到的最大金额和。这样你就知道要往哪里递归了

Python代码：

class Solution:
    def rob(self, nums: List[int]) -> int:
        n = len(nums)
        def dfs(i):
            if i<0:
                return 0
            res = max(dfs(i-1),dfs(i-2)+nums[i]);
            return res
        return dfs(n-1)

C++代码：

class Solution {
public:
    // 回溯
    int rob(vector<int>& nums) {
        int n = nums.size();
        function<int(int)>dfs = [&](int i) -> int {
            if(i<0) return 0;
            return max(dfs(i-1),dfs(i-2)+nums[i]);
        };
        return dfs(n-1);
    }
};

超出时间限制

在定义DFS 或者 DP 数组的含义时，它只能表示从一些元素中算出结果，而不是从一个元素中算出结果，另外一点是：没有把得到的金额和作为递归的入参，而是把它当做了返回值，后面在写记忆化的时候，就明白为什么了？接着往下看~

（三）递归搜索 + 保存计算结果 = 记忆化搜索

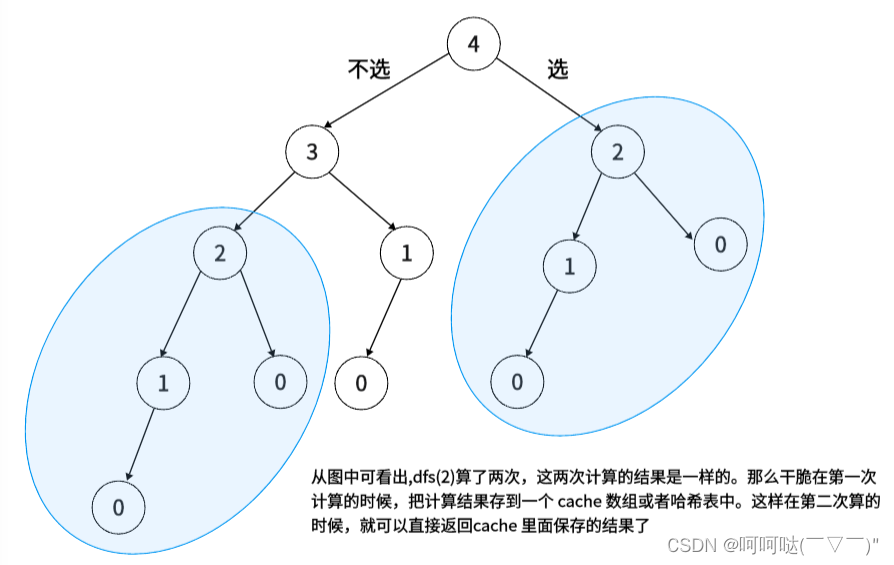
从图中可看出,dfs(2)算了两次，这两次计算的结果是一样的。那么干脆在第一次计算的时候，把计算结果存到一个 cache 数组或者哈希表中。这样在第二次算的时候，就可以直接返回 cache 里面保存的结果了

把递归的计算结果保存下来，那么下次递归到同样的入参时就直接返回先前保存的结果

递归搜索 + 保存计算结果 = 记忆化搜索

可以看到优化后这颗搜索树只有 O(n) 个节点，因此时间复杂度也优化到了 O(n)

Python代码：

class Solution:
    def rob(self, nums: List[int]) -> int:
        n = len(nums)
        # 用cache,它的原理是用一个hashmap记录入参和对应的返回值（对于这份代码，也可以用数组来实现）
        @cache
        def dfs(i):
            if i<0:
                return 0
            res = max(dfs(i-1),dfs(i-2)+nums[i]);
            return res
        return dfs(n-1)

class Solution:
    def rob(self, nums: List[int]) -> int:
        n = len(nums)
        cache = [-1] * n
        def dfs(i):
            if i<0:
                return 0
            if cache[i]!=-1:
                return cache[i]
            res = max(dfs(i-1),dfs(i-2)+nums[i])
            cache[i] = res
            return res
        return dfs(n-1)

C++代码：

class Solution {
public:
    int rob(vector<int> &nums) {
        int n = nums.size();
        vector<int> memo(n, -1); // -1 表示没有计算过
        // dfs(i) 表示从 nums[0] 到 nums[i] 最多能偷多少
        function<int(int)> dfs = [&](int i) -> int {
            if (i < 0) return 0; // 递归边界（没有房子）
            if (memo[i] != -1) return memo[i]; // 之前计算过
            return memo[i] = max(dfs(i - 1), dfs(i - 2) + nums[i]);
        };
        return dfs(n - 1); // 从最后一个房子开始思考
    }
};

class Solution {
public:
    // 记忆化递归
    int rob(vector<int>& nums) {
        int n = nums.size();
        vector<int> memo(n,-1);
        function<int(int)>dfs = [&](int i) -> int {
            if(i<0) return 0;
            int& res = memo[i];
            if(res != -1) return res;
            return res=max(dfs(i-1),dfs(i-2)+nums[i]);
        };
        return dfs(n-1);
    }
};

class Solution {
public:
    // 记忆化递归
    int rob(vector<int>& nums) {
        int n = nums.size();
        vector<int> memo(n+2,-1);
        function<int(int)>dfs = [&](int i) -> int {
            if(i<0) return 0;
            int &res = memo[i];
            if(res != -1) return res;

            int& x = memo[i+1];
            if(x == -1) x = dfs(i-1);
            
            int& y = memo[i+2];
            if(y == -1) y = dfs(i-2)+nums[i];

            return res=max(x,y);
        };
        return dfs(n-1);
    }
};

时间复杂度：O(n)，其中 n 为 nums 的长度
空间复杂度：O(n)

（四）1:1 翻译成递推

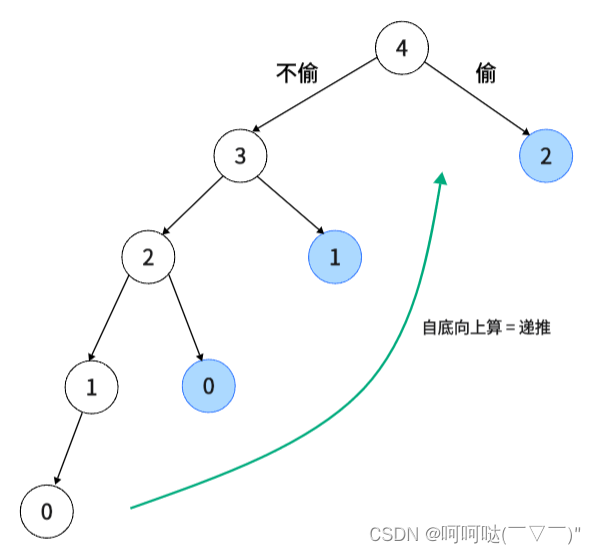
自顶向下算 = 记忆化搜索
自底向上算 = 递推

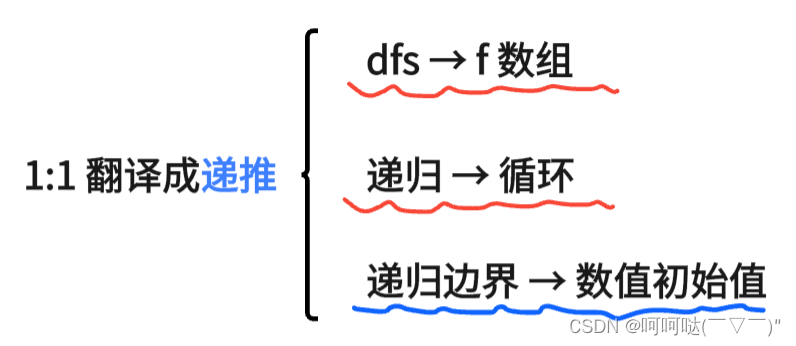
怎么把记忆化搜索改成递推呢？把 $dfs$ 改成 $f$ 数组，把「递归」改成「循环」就好了。但这样写的话，需要对 $i = 0$ 和 $i = 1$ 的情况特殊处理，因为这里会产生负数下标。为了避免出现负数下标，你可以把 $i$ 改成从 2 开始，也可以把这三处的 $i$ 都加 2 ，得到如下式子

$dfs(i) = max(dfs(i-1),dfs(i-2)+nums[i]));$
$f[i] = max(f[i-1],f[i-2] + nums[i]);$
$f[i+2] = max(f[i+1],f[i] + nums[i]);$

Python代码:

# 空间复杂度:O(n)
class Solution:
    def rob(self, nums: List[int]) -> int:
        n = len(nums)
        f = [0] * (n+2)
        for i,x in enumerate(nums):
            f[i+2] = max(f[i+1],f[i]+x);
        return f[n+1]

C++代码：

class Solution {
public: 
    // 1:1 翻译成递推：f[i+2] = max(f[i+1],f[i]+nums[i]);
    int rob(vector<int>& nums) {
        int n = nums.size();
        vector<int> f(n+2,0);
        for(int i=0;i<n;i++) 
            f[i+2] = max(f[i+1],f[i]+nums[i]);
        return f[n+1];
    }
};

时间复杂度：O(n)，其中 n 为 nums 的长度
空间复杂度：O(n)

思考：如何把空间复杂度优化成 O(1) 呢?

要计算 $f(i)$ ，只需要直到它的 上一个 状态和 上上一个 状态的值，此外对于 $f(i+1)$ 来说， $f(i)$ 就变成它的上一个状态了， $f(i-1)$ 就变成了它的上上一个状态了。那么用 $f0$ 表示「上上一个」， $f1$ 表示「上一个」 就可以变成这个式子：

当前 = max(上一个，上上一个 + nums[i])
$f0$ 表示 上上一个， $f1$ 表示 上一个
$newF = max(f1,f0+nums[i])$
$f0 = f1$
$f1 = newF$

算出 $newF$ 之后，就要准备计算下一个了，此时 $f1$ 就变成了上上一个， $newF$ 就变成了上一个

# 空间复杂度:O(1)
class Solution:
    def rob(self, nums: List[int]) -> int:
        n = len(nums)
        f0 = f1 = 0
        for i,x in enumerate(nums):
            new_f = max(f1,f0+x);
            f0=f1
            f1=new_f
        return f1

C++代码：

class Solution {
public:
    // 空间优化
    int rob(vector<int>& nums) {
        int n = nums.size();
        int f0=0,f1=0;
        for(const int& x:nums) {
            int new_f = max(f1, f0 + x);
            f0 = f1;
            f1 = new_f;
        }
        return f1;
    }
};

时间复杂度：O(n)，其中 n 为 nums 的长度
空间复杂度：O(1)，仅用到若干额外变量

参考和推荐文章、视频：

198. 打家劫舍 - 力扣（LeetCode）https://leetcode.cn/problems/house-robber/solutions/2102725/ru-he-xiang-chu-zhuang-tai-ding-yi-he-zh-1wt1/动态规划入门：从记忆化搜索到递推_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Xj411K7oF/?spm_id_from=333.788&vd_source=a934d7fc6f47698a29dac90a922ba5a3