残差网络的提出,是为了解决深度学习中的退化问题。

退化问题指的是随着神经网络层数的增加，网络性能反而逐渐降低的现象。换句话说，当我们不断增加神经网络的层数时，神经网络的训练误差可能会持续下降，但是验证集误差却不断增加，最终网络性能达到瓶颈。

退化问题的原因可以归结为深层神经网络的优化难度和特征复杂度的变化。在深层神经网络中，梯度消失和梯度爆炸问题可能会导致参数更新不稳定，使得网络无法充分学习。同时，深层网络的特征空间也更为复杂，网络学习更加困难，容易遇到过拟合等问题。

为什么残差网络可以解决退化问题?

传统的网络结构,输出H(x) = F(x),而残差网络引入短路连接或称为跳跃连接,使得输出H(x) = F(x) + x在深度神经网络中,随着训练过程中反向传播权重参数的更新,网络中某些卷积层已经达到最优解了,此时这些层的输入和输出差别不大,已经没有训练的必要了,所以我们可以设F(x) = 0,这时H(x) = x就是最优输出。

在传统的网络结构中，即便网络训练已经达到最优解了，但是随着网络继续训练、权重参数的更新，有可能将已经达到最优解的权重参数继续更新为误差更多的值。引入短路连接后，在达到最优解的时候直接通过F(x)=x,那么权重参数可以达到至少不会比之前训练效果差的目的，并且可以加快网络收敛。

在解决梯度消失的问题上,可以通过以下公式分析:

                ​​​​​​​        ​​​​​​​        ​​​​​​​        

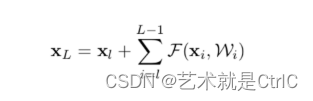
其中XL是现有网络的某个深层的卷积层,Xl表示某个残差的输入层

在反向传播中,残差网络的梯度公式求导后如下:

        ​​​​​​​        

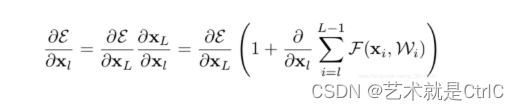
可以看出,即使多层网络中连乘而可能引起梯度消失问题,但是由于多了对x的直接映射,梯度为1,就能避免梯度消失问题。