6-7 二叉树的非递归遍历分数 10

news2024/11/24 3:52:59

文章目录

1.非递归前序遍历
- 1.1C++写法及解析
- 1.2本题ac答案
2.非递归中序遍历
2.非递归后序遍历
- 2.1栈模拟实现非递归
- - C++写法
  - 本题ac答案
  - 本题flag标记法
- 2.2逆序思想
- 2.3整体代码

在这里插入图片描述

1.非递归前序遍历

1.1C++写法及解析

vector<int> preorderTraversal(TreeNode* root)
{
    vector<int> v;       //v存储遍历结点的数据
    stack<TreeNode*> st; //st是一个栈对象 存储数据类型是结点的指针
    TreeNode* cp = root;
    while (cp || !st.empty())
    {
        //遍历到最左结点
        while (cp)
        {
            //一路记录数据作为遍历结果
            v.push_back(cp->val);
            //一路记录指针便于回溯
            st.push(cp);

            cp = cp->left;
        }

        //while循环结束 此时遍历到最左结点
        
        //栈顶结点出栈 访问栈顶结点的右子树
        TreeNode* top = st.top();
        cp = top->right;
        st.pop();
    }

    return v;
}

在这里插入图片描述

1.2本题ac答案

void PreorderTraversal(BinTree BT)
{
    Stack st = CreateStack();
    BinTree cp = BT;
    while (cp || !IsEmpty(st)) 
    {
        while (cp) 
        {
            printf(" %c", cp->Data);
            Push(st, cp);
            cp = cp->Left;
        }
        cp = Pop(st);
        cp = cp->Right;
    }
}

2.非递归中序遍历

在这里插入图片描述

void InorderTraversal(BinTree BT) 
{
    Stack st = CreateStack();
    BinTree cp = BT;
    while (cp || !IsEmpty(st))
    {
        //遍历到最左结点
        while (cp) 
        {
            //一路记录指针便于回溯
            Push(st, cp);
            cp = cp->Left;
        }
        
        //此时已到最左结点

        //假定最近一次遍历到的结点为x
        // 将x出栈 记录x指针
        // 1.将x出栈: x已在正确的顺序中被遍历 已无用
        // 2.记录x指针: 访问x数据 且 要访问x的右子树
        
        //出栈 记录指针
        cp = Pop(st);
        //访问数据
        printf(" %c", cp->Data);
        //访问右子树
        cp = cp->Right;

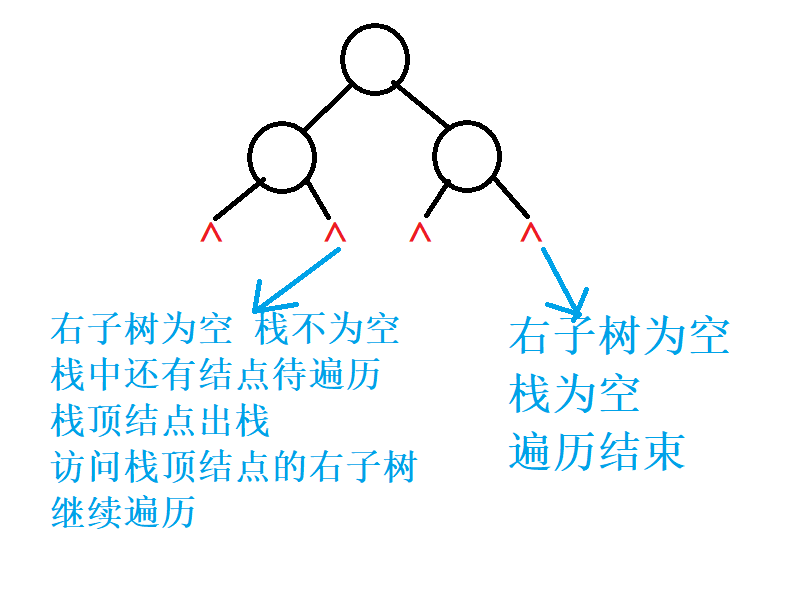
        //右空栈不空 还有结点待遍历 执行下一次大while循环
        //右空栈空 遍历结束
    }
}

2.非递归后序遍历

2.1栈模拟实现非递归

C++写法

vector<int> postorderTraversal(TreeNode* root)
{
    vector<int> v;
    stack<TreeNode*> st;
    TreeNode* cp = root;
    TreeNode* prv = nullptr;

    while (cp || !st.empty())
    {
        //一路遍历并记录指针到最左结点
        while (cp)
        {
            st.push(cp);
            cp = cp->left;
        }
        //while循环结束 已到最左结点 cp指向最左结点左孩子(null)
        

        对栈顶结点进行判断并处理

        TreeNode* top = st.top();
        //左已经为空 若右也空 左右已遍历结束 需要访问根
        if (top->right == nullptr || top->right == prv)
        {
            //记录当前所访问结点
            prv = top;

            //访问数据
            v.push_back(top->val);
            //出栈
            st.pop();
        }
        else
            cp = top->right;

        //cp仍指向该结点的左孩子(null)
    }

    return v;
};

本题ac答案

void PostorderTraversal(BinTree BT)
{
    Stack st = CreateStack();
    BinTree cp = BT;
    BinTree prv = NULL;

    while (cp || !IsEmpty(st))
    {
        while (cp)
        {
            Push(st, cp);
            cp = cp->Left;
        }
        BinTree top = Peek(st);
        if (top->Right == NULL || top->Right == prv)
        {
            prv = top;
            printf(" %c", top->Data);
            Pop(st);
        }
        else
            cp = top->Right;
    }
}

本题flag标记法

void PostorderTraversal(BinTree BT)
{
    if (BT == NULL)
        return;

    Stack st = CreateStack();
    BinTree cp = BT;
    cp->flag = 0;

    while (cp || !IsEmpty(st))
    {
        //一路遍历并记录指针到最左结点
        while (cp)
        {
            Push(st, cp);
            cp->flag++;//表示左子树已被遍历

            cp = cp->Left;
        }

        cp = Peek(st);
        if (cp->flag == 2)  //左右子树都被遍历
        {
            //访问
            printf(" %c", cp->Data);
            //出栈
            Pop(st);

            //神来之笔: 
            // cp置空表示当前子树已被访问完
            // 需要访问下一个栈顶即上一个结点
            cp = NULL;
        }
        else
        {
            cp->flag++;
            cp = cp->Right;
        }
    }
}

2.2逆序思想

前序遍历顺序: 根左右
后序遍历顺序: 左右根

对于正向思维我们在上述2.1看到需要判断右子树是否已经遍历过有两种方法:

在二叉树中结点类中加一个flag状态标记若一个结点的左右子树都已访问则flag == 2(实际上这种方法不建议使用因为二叉树的有效数据应为数据域+指针域直接在二叉树中加一个flag实在是有伤大雅)
搞一个prv指针指向上一个访问过的top 下次访问右子树时判断是否已访问

逆序思维是怎样的呢?

如果我们能以根右左的顺序遍历最后逆序就可以成功完成后序遍历

为什么逆序思维不用判断特殊情况?比如设置个flag或者搞一个prv?

逆序思维思想: 根先入栈访问根根出栈左右子树依次入栈此时栈中存放的结点顺序为: 左孩子右孩子 因为栈先进后出的特性栈顶可以先访问他的右孩子右孩子入栈访问右孩子左右子树入栈…

有的同学可能就会问了那为什么不直接正序呢? 比如: 根先不入栈按右子树左子树的顺序入栈这样不是可以正向输出吗?

有这样问题的同学明显忽略了逆序思维的触发条件: 栈不空在栈不空的条件下进行逆序操作如果正向操作当左右子树都访问完没办法在最后去访问根但是逆序思维却可以在最开始访问到根最后反转访问到的数据

class Solution
{
public:
    vector<int> postorderTraversal(TreeNode* root)
    {
        vector<int> v;
        stack<TreeNode*> st;
        //对于每一个结点: 
        // 入栈--top指向该结点--出栈-- 1. top不空--访问数据并将其左右子入栈
        //                          2. top空--不用访问数据不用将其左右子入栈
        st.push(root);

        while (!st.empty())
        {
            TreeNode* top = st.top();
            st.pop();

            if (top != nullptr)
                v.push_back(top->val);
            else
                continue;

            st.push(top->left);
            st.push(top->right);
        }

        reverse(v.begin(), v.end());

        return v;
    }
};

2.3整体代码

void InorderTraversal(BinTree BT) 
{
    Stack st = CreateStack();
    BinTree cp = BT;
    while (cp || !IsEmpty(st))
    {
        while (cp) 
        {
            Push(st, cp);
            cp = cp->Left;
        }
        cp = Pop(st);
        printf(" %c", cp->Data);
        cp = cp->Right;
    }
}
void PreorderTraversal(BinTree BT)
{
    Stack st = CreateStack();
    BinTree cp = BT;
    while (cp || !IsEmpty(st)) 
    {
        while (cp) 
        {
            printf(" %c", cp->Data);
            Push(st, cp);
            cp = cp->Left;
        }
        cp = Pop(st);
        cp = cp->Right;
    }
}
void PostorderTraversal(BinTree BT)
{
    Stack st = CreateStack();
    BinTree cp = BT;
    BinTree prv = NULL;

    while (cp || !IsEmpty(st))
    {
        while (cp)
        {
            Push(st, cp);
            cp = cp->Left;
        }
        BinTree top = Peek(st);
        if (top->Right == NULL || top->Right == prv)
        {
            prv = top;
            printf(" %c", top->Data);
            Pop(st);
        }
        else
            cp = top->Right;
    }
}