数据结构与算法—“二叉树”的实现

一、二叉树链式结构的实现

1、声明结构体

2、创建新节点

3、创建二叉树

二、二叉树的遍历

1、前序遍历讲解

2、节点个数

3、叶子节点个数

4、二叉树的高度

5、第k层节点个数

6、查找值为x的节点

完整版代码：

一、二叉树链式结构的实现

1、声明结构体

我们为二叉树的节点创建BTNode结构体，成员包含数据data、左节点和右节点的指针。

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

2、创建新节点

为新节点分配空间并初始化。

BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}

	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}

3、创建二叉树

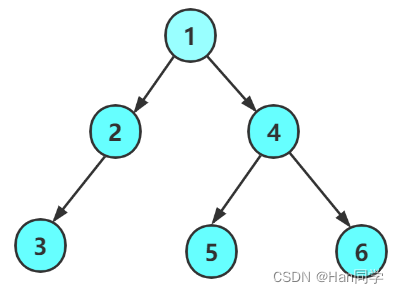
我们创建七个节点，将它们连接起来，使其成为下图的形态：

BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	BTNode* node7 = BuyNode(7);


	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	node5->left = node7;

	return node1;
}

二、二叉树的遍历

二叉树的遍历是一种系统地访问其所有节点的方法，这对于深入理解树的结构和特性至关重要。

遍历，本质上，是按照某一确定的次序，逐一访问二叉树中的每个节点，确保每个节点都被访问一次，并且只被访问一次。这种访问操作可以是任何针对节点的处理，具体取决于应用场景。

基于节点访问的先后次序，二叉树的遍历可以分为前序、中序和后序三种主要类型：

前序遍历（亦称为先序遍历）：首先访问根节点，然后遍历左子树，最后遍历右子树。
中序遍历：首先遍历左子树，然后访问根节点，最后遍历右子树。
后序遍历：首先遍历左子树，然后遍历右子树，最后访问根节点。

这三种遍历方法都采用递归的方式来访问节点，为我们提供了一个明确且系统的方式来处理和理解二叉树。

我们用刚刚创建的二叉树来写出前、中、后序：

接下来，我们用代码实现遍历，验证咱们书写的前、中、后序是否正确：

1、前序遍历讲解

我们以前序遍历的方法为例进行讲解，中序和后序的遍历方法与其大同小异。

void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

接收参数为根节点。
如果当前节点为空则输出打印N（表示NULL），不为空则输出当前节点的值。
递归调用PrevOrder函数遍历当前节点的左子树。
递归调用PrevOrder函数遍历当前节点的右子树。

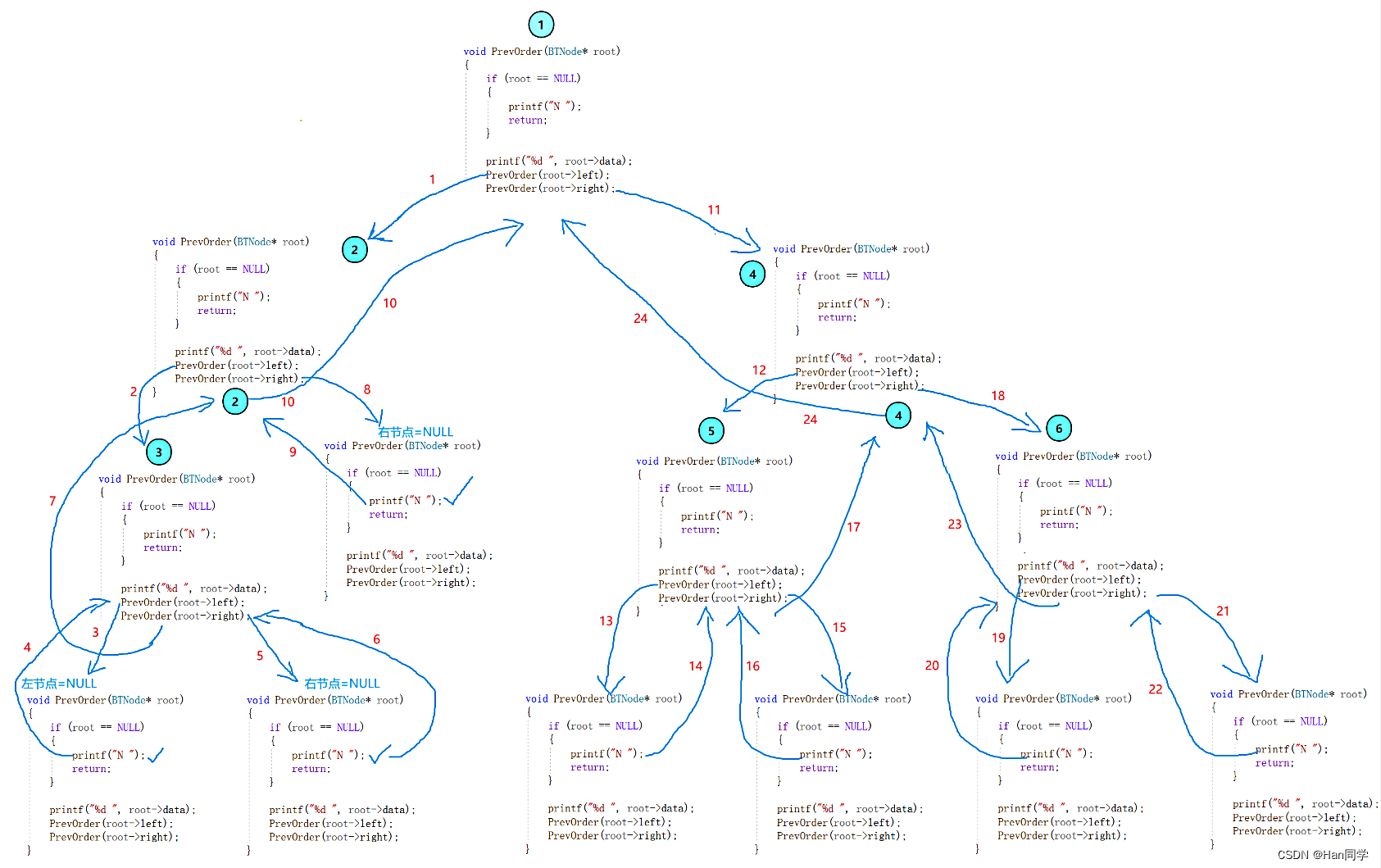
函数会将当前节点的左子节点和右子节点作为参数传递给自身。这样，PrevOrder函数就可以在遍历完当前节点后，继续遍历左右子树。当遍历到叶子节点时，PrevOrder函数会直接返回，结束递归调用。

递归全过程如下图：（红色数字表示递归顺序）

前、中、后序遍历完整代码：

void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

void InOrder(BTNode* root)
{
	if (root == NULL) {
		printf("N ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

void PostOrder(BTNode* root)
{
	if (root == NULL) {
		printf("N ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

int main()
{
	BTNode* root = CreatBinaryTree();
	PrevOrder(root);
	printf("\n");

	InOrder(root);
	printf("\n");

	PostOrder(root);
	printf("\n");
    return 0;
}

根据输出结果可知我们之前的计算结果正确！！！

2、节点个数

以下两种方式都可以，第二种比较简洁，二者效果相同。

int BTreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;

	return BTreeSize(root->left)
		+ BTreeSize(root->right)+ 1;
}

int BTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BTreeSize(root->left)
		       + BTreeSize(root->right) + 1;
}

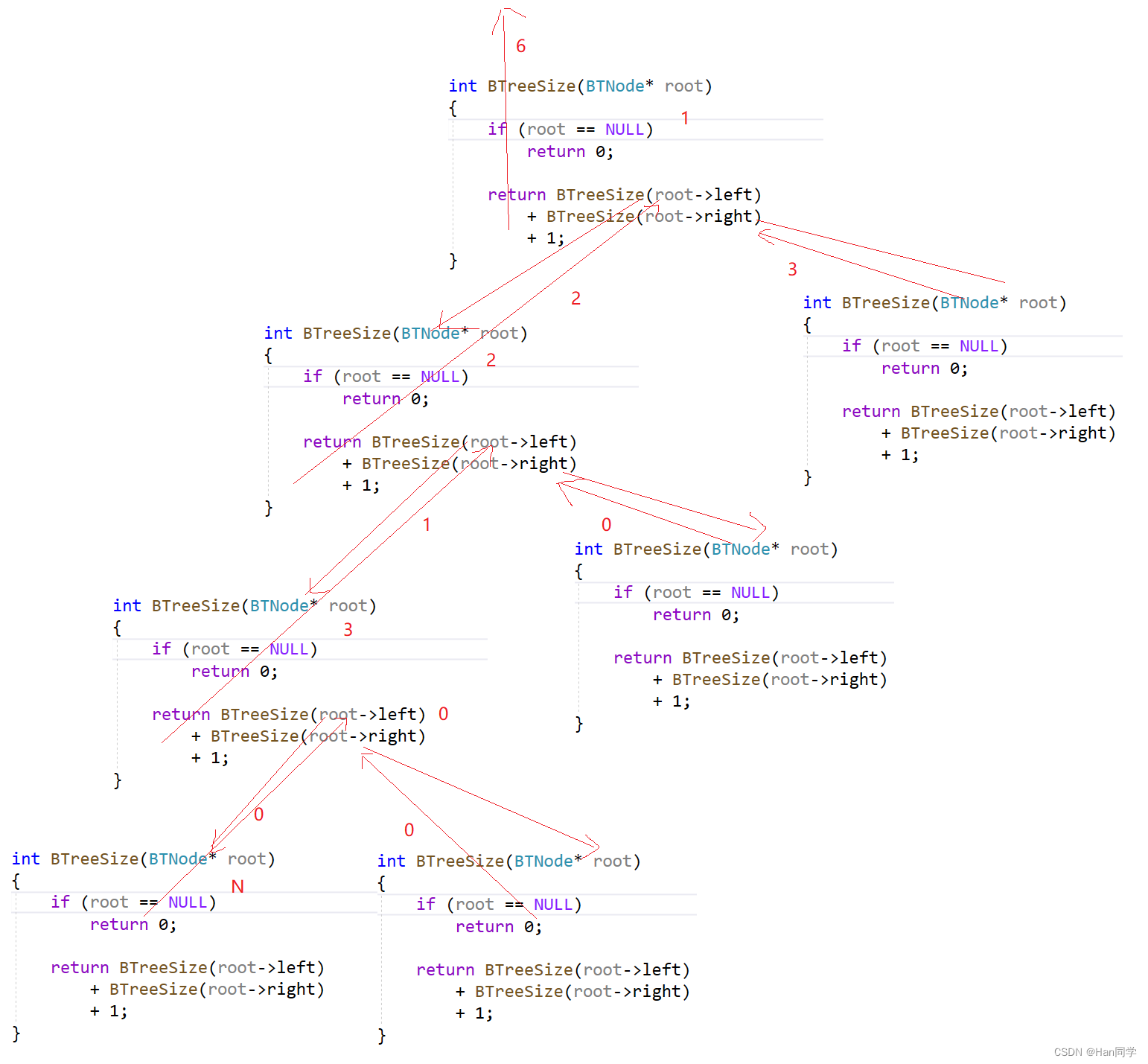
在函数内部，首先判断当前节点是否为空，
如果为空则返回0。
如果当前节点不为空，则递归调用BTreeSize函数计算当前节点的左子树和右子树中节点的个数，然后将它们相加，并加上当前节点本身，即可得到整个二叉树中节点的个数。

3、叶子节点个数

int BTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;

	if (root->left == NULL && root->right == NULL)
		return 1;

	return BTreeLeafSize(root->left)
		+ BTreeLeafSize(root->right);
}

在函数内部，首先判断当前节点是否为空，如果为空则返回0。如果当前节点不为空，则判断当前节点是否为叶子节点。
如果当前节点是叶子节点，则返回1。
如果当前节点不是叶子节点，则递归调用BTreeLeafSize函数计算当前节点的左子树和右子树中叶子节点的个数，然后将它们相加，即可得到整个二叉树中叶子节点的个数。

4、二叉树的高度

int BTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;

	int leftHeight = BTreeHeight(root->left);
	int rightHeight = BTreeHeight(root->right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

在函数中，首先判断当前节点是否为空。

如果当前节点为空，返回0。

如果当前节点不为空，则递归计算其左右子树的高度，分别保存在leftHeight和rightHeight变量中。

最后，通过比较左右子树的高度，得到较大值并加1，即为整个二叉树的高度。
这里使用了三目运算符，如果leftHeight大于rightHeight，则返回leftHeight+1，否则返回rightHeight+1。

5、第k层节点个数

int BTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0);

	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;

	return BTreeLevelKSize(root->left, k - 1)
		+ BTreeLevelKSize(root->right, k - 1);
}

在函数内部，首先判断当前节点是否为空，如果为空则返回0。
如果当前节点不为空，则判断当前层数是否为1。
如果当前层数为1，则返回1。
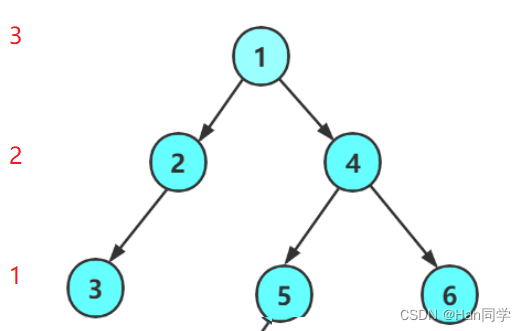
（图中假设求第三层节点个数，左侧红色数字为函数内k随层数的变化）
如果当前层数不为1，则递归调用BTreeLevelKSize函数计算当前节点的左子树和右子树中第k-1层节点的个数，然后将它们相加，即可得到整个二叉树中第k层节点的个数。

6、查找值为x的节点

BTNode* BTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;

	if (root->data == x)
		return root;
	
	BTNode* ret1 = BTreeFind(root->left, x);
	if (ret1)
		return ret1;

	BTNode* ret2 = BTreeFind(root->right, x);
	if (ret2)
		return ret2;
	
	return NULL;
}

在函数中，首先判断当前节点是否为空。

如果当前节点为空，说明已经遍历到叶子节点仍未找到目标值，返回NULL。

如果当前节点的值等于目标值x，说明已经找到了目标节点，返回该节点指针。

如果当前节点不是目标节点，则递归查找其左右子树。

首先在左子树中查找目标值，如果找到则返回该节点指针；

如果在左子树中未找到，则在右子树中查找目标值，如果找到则返回该节点指针。

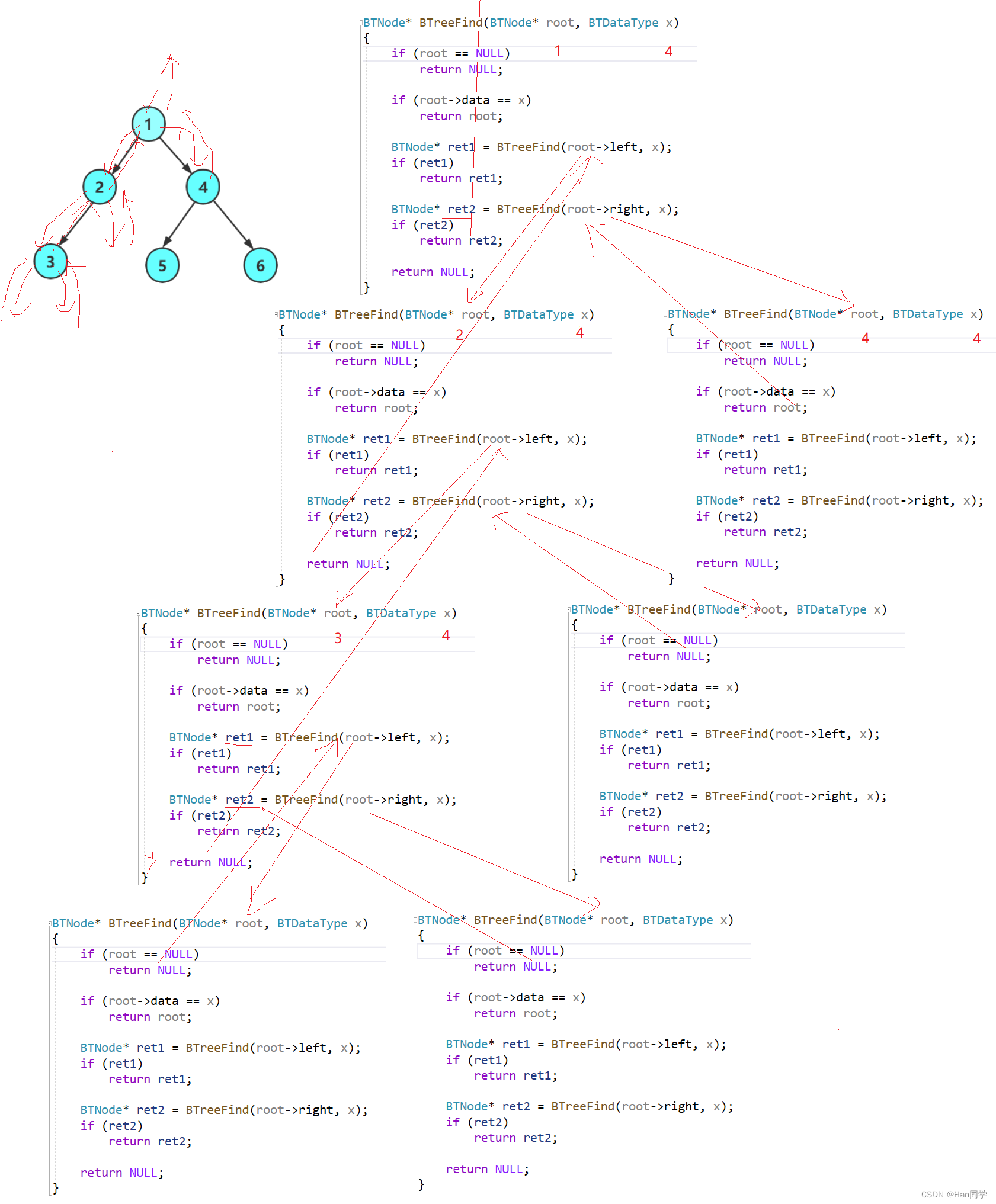
如果左右子树中都未找到目标值，则返回NULL。

查找值为 4 的节点过程如下：

完整版代码：

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL) {
		perror("malloc fail");
		return;
	}
	node->data = x;
	node->left = node->right = NULL;
	return node;
}

BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	//BTNode* node7 = BuyNode(7);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	//node5->left = node7;

	return node1;
}

void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

void InOrder(BTNode* root)
{
	if (root == NULL) {
		printf("N ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

void PostOrder(BTNode* root)
{
	if (root == NULL) {
		printf("N ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

int BTreeSize(BTNode* root)
{
    //两种都可以
	/*if (root == NULL)
		return 0;

	return BTreeSize(root->left)
		+ BTreeSize(root->right)
		+ 1;*/

	return root == NULL ? 0 : BTreeSize(root->left)
		+ BTreeSize(root->right) + 1;
}

int BTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	if (root->left == NULL
		&& root->right == NULL)
	{
		return 1;
	}

	return BTreeLeafSize(root->left)
		+ BTreeLeafSize(root->right);
}

int BTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;

	int leftHeight = BTreeHeight(root->left);
	int rightHeight = BTreeHeight(root->right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}


int BTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0);

	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;

	return BTreeLevelKSize(root->left, k - 1)
		+ BTreeLevelKSize(root->right, k - 1);
}

BTNode* BTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;

	if (root->data == x)
		return root;
	
	BTNode* ret1 = BTreeFind(root->left, x);
	if (ret1)
		return ret1;

	BTNode* ret2 = BTreeFind(root->right, x);
	if (ret2)
		return ret2;
	
	return NULL;
}

int main()
{
	BTNode* root = CreatBinaryTree();
	PrevOrder(root);
	printf("\n");

	InOrder(root);
	printf("\n");

	PostOrder(root);
	printf("\n");

	//printf("BTreeSize:%d\n", BTreeSize(root));

	//printf("BTreeLeafSize:%d\n", BTreeLeafSize(root));

	//printf("BTreeLeafSize:%d\n", BTreeLeafSize(root));

	//printf("BTreeLevelKSize:%d\n", BTreeLevelKSize(root, 3));
	//printf("BTreeLevelKSize:%d\n", BTreeLevelKSize(root, 4));

	return 0;
}