Colorful Image Colorization灰度图像上色

在这里插入图片描述

论文标题：https://arxiv.org/pdf/1603.08511.pdf
论文地址：https://arxiv.org/pdf/1603.08511.pdf
github地址：https://github.com/richzhang/colorization

论文信息概要

问题描述和背景

本文的研究问题是如何将灰度照片变成逼真的彩色图像。这个问题非常具有挑战性，因为灰度图像已经失去了大部分的颜色信息。然而，作者指出，在许多情况下，场景的语义和纹理信息仍然提供了有关颜色的线索，例如，草地通常是绿色的，天空通常是蓝色的。因此，研究目标不是还原精确的真实颜色，而是生成一个能愚弄人类观察者的合理上色效果。

解决方法

为了解决上述问题，作者提出了一种全自动的方法，将其视为一个分类任务，通过训练数据来捕捉语义和纹理之间的统计依赖关系，从而生成生动和逼真的彩色图像。作者的方法基于CIE Lab颜色空间中的明度通道L，然后预测a和b颜色通道。训练数据采用大规模的彩色照片，使其具有充足的颜色信息。(通过L映射到a和b的颜色通道类型a = L)

损失函数和多模态性

与以往的方法不同，作者采用了专门针对上色问题的损失函数。由于颜色预测是多模态的，即多个颜色可能对一个对象是合理的，作者采用了一种损失函数，鼓励多种可能颜色的预测，并在训练时重新加权以强调罕见的颜色。最终的上色效果是基于颜色分布的平均值，使得结果更加生动和真实。

评估方法

为了评估上色结果，作者引入了一种新颖的“上色图灵测试”，通过人类参与者的选择来测试合成的彩色图像的视觉逼真度。结果显示，作者的算法成功地愚弄了人类观察者，并产生了接近照片质量的彩色图像。此外，作者还展示了生成的彩色图像在对象分类等下游任务中的实用性。

自监督表示学习

最后，作者将彩色化任务作为自监督表示学习的方法，通过学习从原始数据中提取特征表示，取得了在一些基准测试上的最新性能。

论文方法

定义目标函数

作者的目标是将灰度输入通道 $X$ , $\in R^{H \times W \times 1}$ 映射到关联的两个颜色通道 $Y$ ，即 $\hat Y = F(X)$ 。 $\in R^{H \times W \times 2}$ 为了实现这一任务，作者采用CIE Lab色彩空间，并使用欧氏损失函数来度量预测颜色和真实颜色之间的距离。

然而，由于颜色上色问题具有固有的多模态性和歧义性，欧氏损失函数不够鲁棒，容易产生灰暗和褪色的结果。因此，作者将问题视为多项式分类问题，将ab输出空间分成网格大小为10的区域，学习将输入X映射为可能颜色的概率分布。

在这里插入图片描述
这里， $\hat Y_{h,w}$ 代表预测的颜色， $Y_{h,w}$ 代表真实颜色， $∥ \cdot ∥$ 代表欧氏距离。

这里的颜色上色多模态性，是因为在某个空间内存在多个可能的颜色选项，这些选项可以被认为是不同的颜色模态。在颜色上色的情况下，一个对象的颜色可以在某个范围内有多种可能性，因此问题变得多模态。

就是说我们预测出来的a和b不是一个单一的值，应该是一个符合合的理范围，

类似于一个苹果的颜色可以是红色、绿色、黄色等等，这就是不同的颜色模态。在颜色上色问题中，系统需要从这些多个可能的颜色中选择一个，这使得问题具有多个模式，因此被称为多模态问题。

多项式分类问题原理

假设我们将ab输出空间分成网格，将颜色空间量化为313个离散值，如下图所示：

在这里插入图片描述
如上图所示：

（a）具有10网格尺寸的量化ab颜色空间。共有313个ab对在色域内。
（b）ab值的经验概率分布，以对数刻度显示。
（c）在L条件下，ab值的经验概率分布，以对数刻度显示。（在L为多少的情况下，有哪些ab值的可能）

对于图像（a）来说，对于给定的输入X，模型学习将其映射为可能颜色的概率分布 $\hat Z = g(x)$

$\hat Z \in [0,1]^{H×W×Q}$

其中Q是量化的ab值的数量。Q=313

为了将预测的 $\hat Z$ 与真实情况进行比较，定义了一个函数
$Z=H_{gt}^{−1} (Y)$ ，它将真实颜色 $Y$ 转换为向量 $Z$ ，采用了一种软编码方案。然后，使用多项式交叉熵损失计算其损失值定义为 $L c l (\cdot, \cdot)$ ，公式如下：
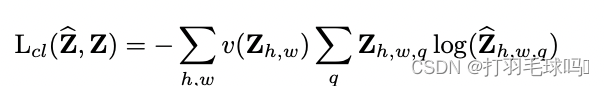
在这里插入图片描述
其中， $v (\cdot)$ 是一个权重项，可以用于根据颜色类别的稀有度来重新平衡损失，

最后，将概率分布 $\hat Z$ 映射到颜色值 $\hat Y$ ，公式如下：
$\hat Y=H(\hat Z)$

软编码方案

上文中提到的软编码方案，这里详细阐述一下

软编码方案是一种用于将颜色标签映射到向量表示的技术，通常用于处理多标签分类问题。在这种情况下，它被用于将颜色标签映射到颜色的概率分布，以便更好地处理多模态的颜色分布。

在文中，软编码方案用于将真实颜色标签（ $Y$ ）映射到向量表示（ $Z$ ），以便与从模型预测的颜色分布（ $Z_b$ ）进行比较。具体来说，对于每个颜色标签，软编码方案会创建一个包含概率值的向量，以表示颜色标签的可能性。这样，一个颜色标签可以与多个不同的颜色概率分布相关联，从而处理多模态性，因为多种颜色可以对应到相同的颜色标签。

软编码方案的实现通常使用softmax函数，将每个可能的颜色标签映射到[0, 1]的概率值，确保它们的总和等于1。这使得可以将颜色标签与颜色分布进行比较，以确定它们的相似性。在这种情况下， $Z$ 是对颜色标签的软编码， $Y$ 是真实颜色标签。然后，通过使用多项式交叉熵损失函数（multinomial cross entropy loss）来比较预测的颜色分布（ $Z_b$ ）和真实的颜色标签的软编码（ $Z$ ），以评估颜色估计的准确性。这个损失函数考虑了颜色类别的稀有度，以便更好地处理颜色类别不平衡的问题。

类别再平衡问题

自然图像中的ab值分布在低ab值方向上有明显偏向，这是因为图像中通常包含了一些低饱和度的背景，比如云、道路、泥土和墙壁等。

上图 (b)展示了从ImageNet的130万张训练图像中收集的ab空间像素的经验分布。可以观察到，自然图像中的低饱和值像素数量比高饱和值像素数量高出几个数量级。如果不考虑这一点，损失函数将被低饱和度的ab值主导，这会导致问题。

为了解决这些问题，作者采用了一种概率分布的方法。首先，他们将ab颜色空间分成一些小的区域，这些区域称为"ab bins"，每个bin代表一组相似的颜色。然后，他们估计了自然图像中每个bin内颜色的出现概率，这构成了一个概率分布，

为了处理颜色分布不平衡的问题，作者引入了权重因子 $w$ ，这些权重因子基于每个像素的颜色稀有度进行计算。这些权重 $w$ 与颜色分布的平滑版本相关，其中低饱和度颜色的权重更高，以平衡不平衡的颜色分布。作者使用高斯核来平滑颜色分布，并将其与均匀分布混合，以生成平滑的经验分布。

具体地，权重 $v(Z_{h,w})$ 计算方式是：
在这里插入图片描述
为得到平滑的经验分布 $\tilde p \in Δ^Q$ ，从完整的ImageNet训练集中估计了量化的ab空间中颜色的经验概率分布 $\in Δ^Q$ ，并使用带有高斯核 $G_\sigma$ 的平滑操作来处理这个分布。然后，将该分布与均匀分布混合，使用权重 $\lambda \in [0,1]$ ，然后取倒数并标准化，以使权重因子在期望上等于1。最后发现 $\lambda = \frac{1}{2}$ 和 $\sigma = 5$ 的值效果很好

类别概率点估计问题

最后，定义了 $H$ ，它将预测的分布 $Y_b$ 映射到ab空间中的点估计。

这个方法涉及如何从预测的颜色分布 $Y_b$ 中获得最终的颜色估计。让我详细解释并提供相关公式：

模式（Mode）方法：对于每个像素，一种选择是从预测的颜色分布中选择具有最高概率的颜色。这个颜色就是该像素的颜色估计，因为它在分布中出现的概率最高。这种方法通常会产生生动但在空间上不一致的结果，因为它会在图像中形成局部高概率点，导致颜色斑点。
- 公式： $Y_b=arg⁡max⁡Y_b$ ，其中arg⁡max⁡表示选择具有最高概率的颜色。
均值（Mean）方法：另一种选择是从预测的颜色分布中计算颜色的平均值。这意味着对于每个像素，从分布中的所有颜色中取加权平均，以获得颜色估计。这种方法通常会产生空间上一致的结果，但颜色可能会过于褪色，呈现不自然的棕褐色调。

- 公式： $Y_b=\frac{1}{Q}\sum_{i=1}^QY_i$ ，其中 $Q$ 是分布中颜色的数量， $Y_i$ 是第 $i$ 个颜色的估计。

退火均值（Annealed-Mean）方法：为了克服模式和均值方法各自的缺点，作者提出了一种插值方法。他们重新调整了softmax分布的温度参数 $T$ ，并计算加权平均，以获得最终的颜色估计。这个过程受到模拟退火技术的启发，因此称为取分布的退火均值。这个方法和图像的稳定扩散有点相似呀。
- 公式： $H(Z_{h,w})=E[f_T(Z_{h,w})]$ ，其中 $f_T(Z)=\frac{exp(log(z)/T)}{\sum_qexp(log(z_q)/T)}$ ， $Q$ 是分布中颜色的数量， $T$ 是温度参数。作者发现将温度参数 $T$ 设置为0.38时，效果最佳。这个温度值产生了在颜色饱和度和空间一致性之间的平衡，从而获得了视觉上令人满意的颜色估计。

最终，作者的系统是由卷积神经网络 $G$ 产生的预测颜色分布与取分布的退火均值操作 $H$ 组合而成的。这个系统允许从灰度图像生成最终的彩色估计。虽然它不是完全端到端可训练的，但 $H$ 操作对每个像素独立操作，只有一个参数，可以作为CNN的前向传递的一部分实现。

在这里插入图片描述

实验结果

在这项研究的实验中，作者首先对算法的图形效果进行了评估，评估了颜色上色的感知真实性以及其他准确性指标。他们与几种不同的变体、以及最近的研究和并行研究进行了比较。然后，他们测试了颜色上色作为自监督表示学习的方法。最后，他们展示了在传统的黑白图像上的定性示例。

具体实验结果如下：

训练数据：作者在ImageNet的训练集中使用了1.3百万张图像来训练他们的网络。
评估数据：他们在ImageNet验证集的前10,000张图像上进行了验证，然后在验证集中的另外10,000张图像上进行了测试。
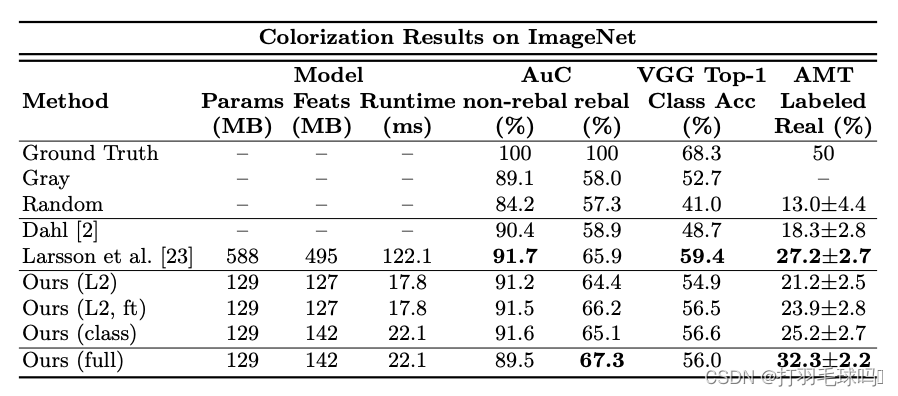
实验结果：在如下表格中提供了定量结果，使用了三个不同的度量标准来评估他们的算法。

作者进行了不同损失函数的实验，以特别测试它们的影响。他们还与之前的方法和并行方法进行了比较，这两者都使用了在ImageNet上训练的CNN。

以下是他们的实验结果使用的不同损失函数方法：

Ours (full)：作者的完整方法，使用分类损失，并进行了类别重新平衡。网络是从头开始训练的，使用了k均值初始化，并使用了ADAM求解器，迭代约450,000次。
Ours (class)：作者的网络使用分类损失，但没有进行类别重新平衡（在等式4中，λ=1）。
Ours (L2): 作者的网络从头开始训练，使用L2回归损失。
Ours (L2, ft): 作者的网络首先通过使用完整的分类与重新平衡的网络进行训练，然后进行L2回归损失的微调。
Larsson et al. [23]: 由Larsson等人提出的CNN方法。
Dahl [2]: 以前的模型，使用L2回归损失，并在VGG特征上使用拉普拉斯金字塔进行训练。
Gray: 将每个像素的颜色设为灰色，即（a, b）= 0。
Random: 从训练集中的随机图像复制颜色。