#pic_center

$R_1$

$R^2$

知识框架

No.1 数据操作数据预处理

一、N维数组样例

• 最基础的数据结构
• 从基础开始数据操作;机器学习用的最多的数据结构是n维数组;这是所有的机器学习,神经网络;以及深度学习用的主要的数据结构;
• 最简单是一个0位的数字叫做标量;比如说最简单就是一个1.0;一个浮点运算;它可能表示一个物体的类别;
• 一维的数组叫做向量;比如说这有三个数字;它是一个特征;比如说一个特征向量就是一个样本;把它抽象成一行数字;
• 2D就是一个矩阵;这里有3行3列;就说可以是一个样本的特征矩阵;要是三个样本;每一行表示一个样本;每一列就表示它不同的特征;

• 高纬度数组样例
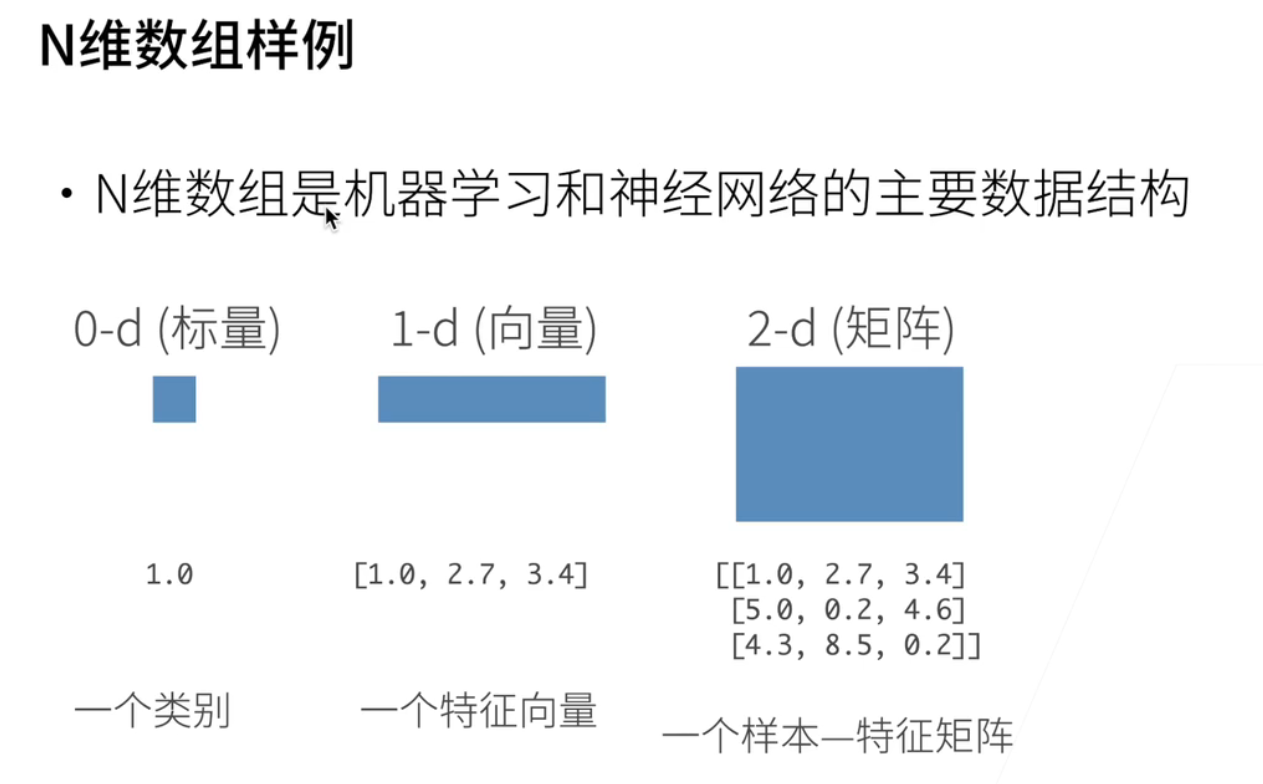
• 3D就是一张图片;RGB的图片是一个三维的数组;因为它有宽度;宽其实是列的个数；高就是你的有多少行;还有r g b三个通道;所以它是一个三维的一个数组;
• 四维就是;n个三维的数组放在一起;比如说一个RGB图片的批量;在深度学习的训练的时候;通常不是一张一张图片去读;通常是比如说每次读128张图片;那就是一个batch(一个批量);
• 数组可以做到五维;现在用的会比较少;比如说一个视频的批量;做视频其实是说很多图片;但是还有个时间的维度;所以是一个批量大小✖时间✖宽高和通道的一个5D的数字;

二、创建数组

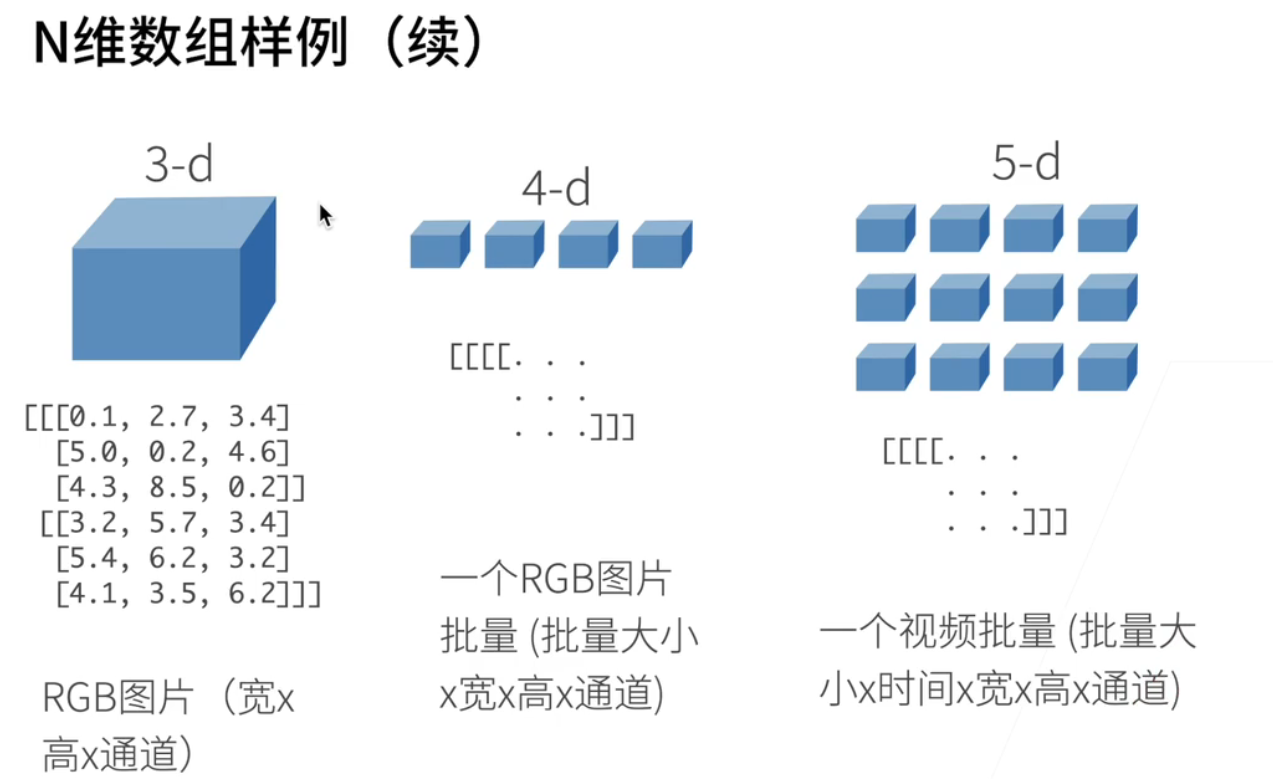
• 创建数组需要给三个东西
• 一个是什么样的形状;比如说一个3*4的一个矩阵;
• 要指定每一个元素的数据类型;比如说一个32位的浮点运算;32位的浮点数;
• 然后要告诉每个元素的值;比如说可以全是0;或者可以全是一个随机数;
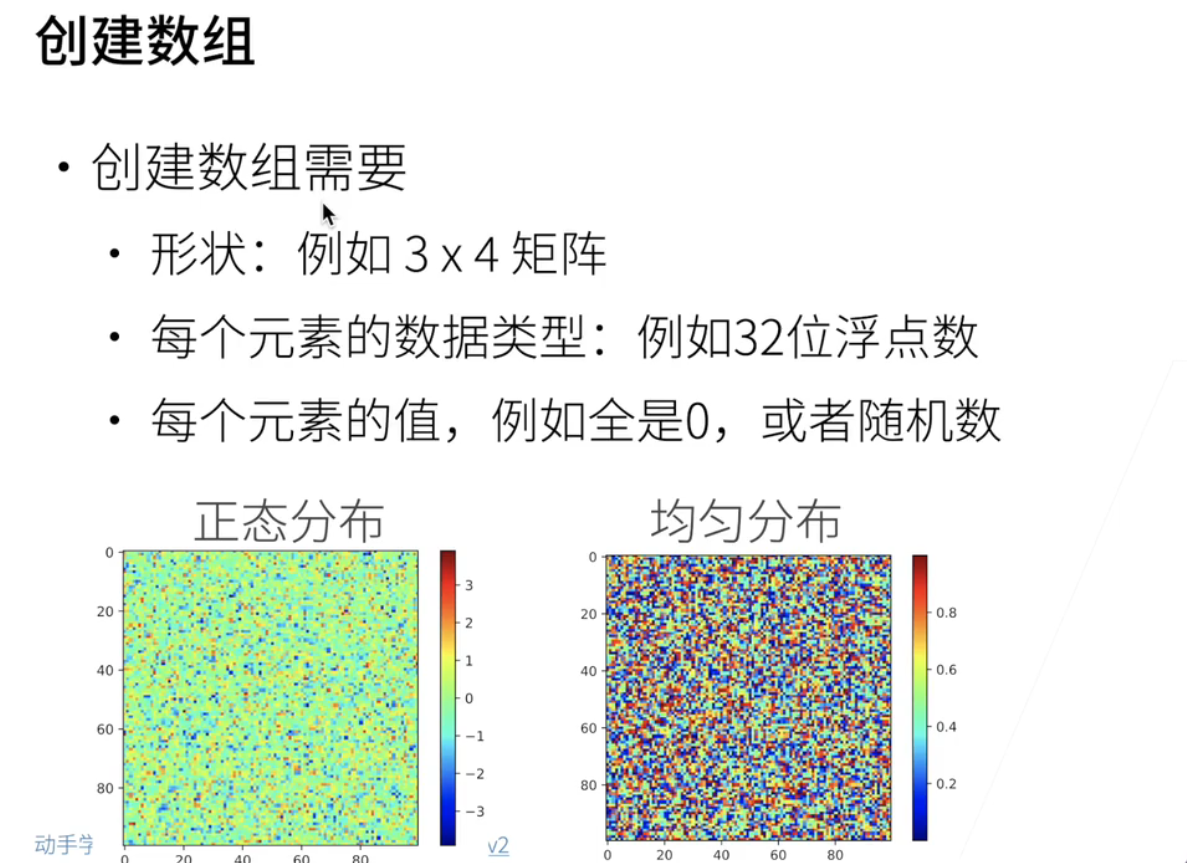
• 下面这两张图表示;左边是说;所有的元素的值;是按照一个正态分布表示的;右边是一个按照均匀分布;就是在0-1之间均匀可以给我出一些值;

三、访问元素

• 几个例子
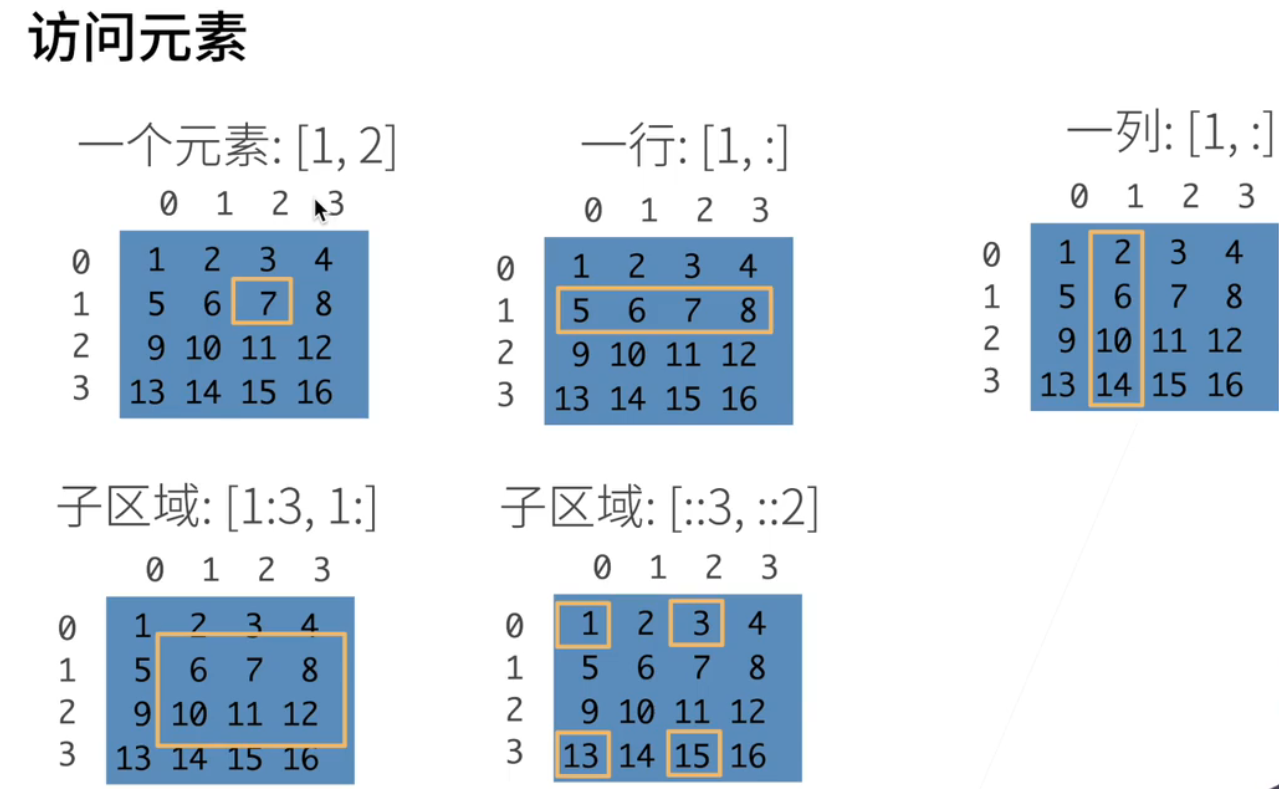
• 第一个是访问第一行：行是从0开始的;1就是第二行; 比如 [1,2] 访问的数据就是7；
• 访问一行;第一行就是通过冒号表示;把这一行所有的列元素访问出来; [ 1,: ]
• 访问一列;就是访问第一列;把所有的行这一块;要把这一列拿出来;：[: ,1 ]
• 拿一个子域;访问是:这是行从第一行开始到;第三行的开区间结束;是拿到的1和2两行;虽然它是3结尾但是它是个开区间;所以是拿到第一行和第二行;然后就是从第一列开始拿到所有的一列;
• 最后一个例子是说要跳的访问;说从第0行到最后一行;但是每3行一跳;就说把第0行拿出来，把第3行拿出来;列的话是每两列一跳;就是把第0列和第2列拿出来;这就是访问一个带跳转的一个子区;

四、数据操作D2L注意点

"""
首先，导入torch。请注意，虽然它被称为PyTorch，但应该导入torch而不是pytorch
要import Pytorch;就是我们叫做Pytorch;但实际上导入的是torch就是Python;
安装的时候也要去安装torch;不要去安装Pytorch在import的时候也要import torch;
"""
import torch
"""
张量表示一个数值组成的数组，这个数组可能有多个维度
举个例子;就是说在torch里面;生成arrange就是从0到12;
把所有的0到12之间从0开始到12前的11结束的所有的东西拿出来;它是一个向量;
就是复制给x然后把x print出来;可以运行一下;
tensor([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])
"""
x = torch.arange(12)
print(x)
"""
可以通过它的shape来访问这个张量的形状;就是x.shape;看到它是一个向量它就是一个维度;
就是说这个维度的长为12;它是一个以维数元素为1的一个数组;
然后它的;number of elements(缩写numel)就是说你里面元素的总数;它永远是个标量就是12;
"""
print(x.shape)
print(x.numel())


"""
如果想改变一个数组或者一个张量的形状;但不改变元素的数量和元素值的话;
可以用reshape;这个函数;刚刚是以12个元素对吧;长为12的向量;
然后可以把它reshape成是有3行和4列;看到它是元素是说它在每一行是连续的;然后把它掐成三行;
这样子我们就是说在0123;然后这样子一个3*4的一个矩阵;
tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]])
torch.Size([3, 4])
12
"""
X = x.reshape(3, 4)
print(X)
print(X.shape)
print(X.numel())

"""
可以创建一些全0的一些函数;就是给形状是234;元素为全0;
然后当然是我们可以元素为全1对吧;可以看到元素为全1;就是形状是234;
tensor([[[0., 0., 0., 0.],
         [0., 0., 0., 0.],
         [0., 0., 0., 0.]],

        [[0., 0., 0., 0.],
         [0., 0., 0., 0.],
         [0., 0., 0., 0.]]])
"""
Y = torch.zeros((2, 3, 4))
print(Y)
Y = torch.ones((2, 3, 4))
print(Y)

"""
要特定的一些值;也可以通过一个Python的列表来复制;我们这里再创建一个二维的一个数组;
这个告诉你是第一行的元素是2143;第二行的元素是1234;然后第三行的元素是啊4321;
然后这是一个列表;然后列表嵌套列表就是一个;list of list单子;我会创建一个二倍的东西出来;
这是一个二维的数字;当然我可以创造一个三维对吧;我再打一个框;放括号就会变成一个三维的数字;
你看到这是一个啊;你可以可以有两个框在这里对吧;如果我要打印它的shape的话;看到是说是一个三维的是134;
"""
print(torch.tensor([[2, 1, 4, 3], 
                    [1, 2, 3, 4], 
                    [4, 3, 2, 1]]))

"""
创建数组后;可以做一些比较常见的标准算数运算;加减乘除和指数;
所有的这些运算都是按元素进行的;所以先从比如说我们创建一个;
我们特别给了一个1.0;就是说这样子;我们创建的是一个浮点运算;就是如果你不你把这个0.1去掉的话;它变成整数了;
其实然后呢我做x加y;他就会按元素全部加起来;你可以认为是3460;
然后做减法按元素做减法;
按元素做乘法;
按元素做除法;
然后按元素求幂;就是对每一个x元素求二次方;
当然是说我还可以做更多计算了;就说我可以做指数对吧;就说按元素来;每个元素做一些指数的运算;
tensor([ 3.,  4.,  6., 10.])
tensor([-1.,  0.,  2.,  6.])
tensor([ 2.,  4.,  8., 16.])
tensor([ 1.,  4., 16., 64.])
tensor([0.5000, 1.0000, 2.0000, 4.0000])
tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])
"""
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
print(x + y)
print(x - y)
print(x * y)
print(x ** y)
print(x / y)
print(torch.exp(x))

"""
我们要把可以做一些张量之间的;或多元数组之间的一些操作;
比如说我们用一个;我们还是一样的生成一个;跟之前一样;
就说生成一个从0到11的元素;长为12的向量;把它reshape到3和4;
这里我们特别指定说你用float 32;就不要给我生成一个integer了
然后呢y也是一个啊;跟刚刚是一样的;是一个3*4的一个运算啊;他们两个的形状是一样的;
然后我们用cat;就是说我把这两个元素合并在一起;然后在第0维合并;就是在行就是你可以认为是在堆起来;
那这看到是说这个;就是说这是我们的第一个生成x;这是我们生成的y;然后我们是在按行上面合并起来;
然后我们可以说dimension等于1;就是按列;
tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.],
        [ 2.,  1.,  4.,  3.],
        [ 1.,  2.,  3.,  4.],
        [ 4.,  3.,  2.,  1.]])

tensor([[ 0.,  1.,  2.,  3.,  2.,  1.,  4.,  3.],
        [ 4.,  5.,  6.,  7.,  1.,  2.,  3.,  4.],
        [ 8.,  9., 10., 11.,  4.,  3.,  2.,  1.]])
"""
X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(torch.cat((X, Y), dim=0))
print(torch.cat((X, Y), dim=1))

"""
然后我们可以通过说;逻辑运算符来构建一个二维的张量;
就说我判一下y是不是等于x;
它就是按元素所谓的按元素值进行判;就说啊就这一个元素;
这两个元素是相等的;别的元素等于是都不相等;

tensor([[False,  True, False,  True],
        [False, False, False, False],
        [False, False, False, False]])
"""
print(X == Y)

"""
tensor(66.)
"""
print(X.sum())

"""

从numpy过来的;就是说一个叫广播机制;
这也是最容易出错的一个地方;就说如果你代码没写好啊;
看上去一切都在运行;实际上可能不是你想象那样子;
比如说;创建一个a;它是一个二维的数组;但是它是一个向量其实它是有三行;它有一列;
然后我创建一个b;它有一行两列你可以打印下去找;这样子对吧;这是a这是b;
我在做a加b;按照我们刚刚的定义;我们是按;a的每个元素和b的每个元素相加;
但它形状不一样啊;不一样怎么加呢;就是说在这个情况下;他有一个特殊的机制来帮你+;
就是说如果当我看到两个张量;有两个多元数组;就我们;其实张量和多元数组是混着用的;
好这两个张量形状不一样;但是呢;我可以有办法把它变成形状一样;为什么呢;
是因为你这里;首先我们的尾数是一样的啊;都是一个纬度等于2都是一个数组;如果你维度不一样就没戏了;因为纬度一样;然后呢第一个纬度我是3但你是一啊;第二个纬度虽然我们不一样;但是我是2你是一;所以的一个半是说;一个办法师说;我可以把我这个一的这一维度;复制一下;复制成两个;然后把我这个跟你不一样的地方;因为我是一嘛;我就可以把我复制成3下;这样子就会把;a复制成一个3*2的一个矩针;把b复制成一个啊3*2的矩针;然后再它相加;这样你可以看到是说;而我们加出来就是一个3*2的矩阵;了这就是一个广播机制;所以是说;很多时候;你如果可能没有想到说我要做广播;就说我就想把两个项链一加;但是你没想到一个项链没弄好;就是加了一个不小心;加了一个纬度和加了一个纬度;它就变成一个矩阵;相加就变成一个矩阵出来了;就不是你想象的那样子;所以这一块就是虽然它很方便;但是大家一定要注意说;有这个机制的存在啊;导致如果有问题的话;大家可能会;去想;这个事情是不是因为广播机制造成的;
tensor([[0],
        [1],
        [2]])
tensor([[0, 1]])
tensor([[0, 1],
        [1, 2],
        [2, 3]])
"""
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
print(a)
print(b)
print(a + b)



"""
然后我们来做一下元素的访问;我们之前有说过说;元素可以做哪些访问啊;
最简单X[-1] 就说把最后一行访问出来;;X[1:3]就是说啊把第一行和啊第二行给拿出来就是X[1:3];
然后我们当然可以是说我要写值;我怎么写呢;我把第一行;就是它其实行还是从0开始啊;
所以第一行其实是说这个是第一行;然后第二列列是从0开始;所以你是写的是这个;是;你把这个元素的值写成9;
然后把x打印出来;你会发现啊别的值呢都没有变;就9就变化了;
tensor([ 8.,  9., 10., 11.])
tensor([[ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.]])
"""
print(X[-1])
print(X[1:3])

"""
最后大概就是说;Python里面最常见的其实既不是pytorch;也不是Tensorflow;其实是numpy;
多元数组的运算框架;就是说;可能大家如果学Python数据编程的话;可能是从numpy学起的;
所以呢当然是所有的;不管是所有的框架;它都能够很方便的从numpy进行转换;
比如说x等于numpy;它会得到一个numpy的一个多元数组;当然你可以torch Tensor;
从一个numpy a拿回来;可以构建一个pytorch的一个Tensor;
你可以看到是说a的type;就是它的类型;它是一个numpy NDRA;
然后它的b是从numpy构建的;所以它是一个torch的一个Tensor;
所以这个是numpy 数据类型;这个是torch的数据类型;
当然如果你是大小唯一的张量的话;我可以变成一个Python的标量;
就是创建一个大小唯一的啊torch的Tensor啊;a当然它就是一个torch的Tensor啦;
OK把a点item拿出来它就是一个啊;number;的一个辅点数啊;当我可以说float a;也是变成一个Python的辅点数
int a;它就变成一个integer就是也是Python的;这就是转变;
<class 'numpy.ndarray'>
<class 'torch.Tensor'>
tensor([3.5000])
3.5
3.5
3
"""
A = X.numpy()
B = torch.tensor(A)
print(type(A))
print(type(B))

a = torch.tensor([3.5])
print(a)
print(a.item())
print(float(a))
print(int(a))

五、数据预处理D2L注意点

"""
数据预处理是说;如果有一个原始数据;我怎么样把它读取进来;
使得我们通过;机器学习的方法能够处理;
这里给一个;几个非常简单的预处理;当之后我们随着课程的加深;我们会介绍更多的一些课程的处理;
首先我们创建一个人工的数据集;存在一个CSV文件里面;这是一个很小很小的文件;
然后呢;接下来就是说;我们把它存在一个CSV文件里面的话;
"""
import os
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
    f.write('NumRooms,Alley,Price\n') # 列名
    f.write('NA,Pave,127500\n') # 每⾏表⽰⼀个数据样本
    f.write('2,NA,106000\n')
    f.write('4,NA,178100\n')
    f.write('NA,NA,140000\n')


"""
我们可以把它读取进来;一般读取CSV文件的话;一般用的是叫做pandas;
这个库也是说啊;作为数据科学家最常使用的一个库;可能它的;使用频率在跟numpy是差不多的频率;
OK我们如果你没有装pandas的话;是一个很小的Python的包;
然后我们import pandas;然后pandas的话;它提供了一个很简单的函数;叫做read CSV;
我们就把刚刚我们读取的文件读取进来;我们就可以打印在print在这个地方;
你会发现这里给你的你的第一行就是你每一个列的名字;接下来是说这有4行;我们运行一下;然后你当然可以print;
   NumRooms Alley   Price
0       NaN  Pave  127500
1       2.0   NaN  106000
2       4.0   NaN  178100
3       NaN   NaN  140000
"""
import pandas as pd
data = pd.read_csv(data_file)
print(data)


"""
接下来是说;注意到我们有一些数据是缺失的;
所以对于数据科学家来说;最重要的一件事情是说;怎么样处理缺失的数据;
或者说整个机器学习就是处理;缺失数据;就是你要预测未来;未来是什么样子;
我们不知道这是一个缺失的数据;当然这这里的话我们先不做预测;我们先说用很简单的方法;
我们把一些缺失的数据补起来啊;补的方法有很多种;最常见的包括如果有一个数据是缺失的话我们就把它丢掉;
把整个这一行丢掉;这是一个最常用的方法;当然很多时候我们说我们丢掉也太可惜了;
然后呢最常用的;这也是一个叫插值的方法;比如说我们这里怎么样进行插值;
首先呢我们数据我们先把它分成一个;输入的特征和输出;但我们现在没有讲;输入特征和输出是什么样子;
那没关系;我们就是说啊对一个data;它是一个;刚刚我们注意到是一个;4乘以3的一个表;
然后我们通过iloc就是index location;来把第一个的第0和第一列;和所有的行拿出来放在input里面;然后把最后一列拿出来放在output里面;
"""
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean())


"""
好那么接下来就是说;因为我们先把所有的缺失的值和所有的字符串全部变成了一个数值;
那么我们就可以变成一个;pytorch的Tensor了;然后我们input torch;
然后;到Tensor我们就把input values放进来;output values放进来;大家可以看到是说OK;
现在我们把一个CSV文件;转成了一个纯的;我们昨天提到过的一个张量了;
注意到这里是float 64;这个传统的Python一般会;默认浮点数会用float 64;但是64为浮点数啊一般计算比较慢;
对深度学习来讲;我们通常用32为浮点数;在这个就是一个非常简单的一个样例;
教大家怎么样把一个;CSV文件读取进来;做一定的特征预处理;然后变成一个pytorch的用的一个Tensor;
(tensor([[3., 1., 0.],
[2., 0., 1.],
[4., 0., 1.],
[3., 0., 1.]], dtype=torch.float64),
tensor([127500, 106000, 178100, 140000]))
"""
import torch
X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
print(X,y)

六、QA

import torch

a = torch.arange(12)
b = a.reshape((3,4))
b[:] = 2
print(a)

"""

tensor([2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
"""

No.2 线性代数

一、标量

• 标量的简单操作
• c=a+b; 然后c=a*b; 然后取个sin;
• 长度的话标量有长度; 就是它绝对值; 如果大于0的话是a; 如果小于0的话就是-a;
• 长度有一些公式; a加b的绝对值小于等于a的绝对值加b的绝对值; a乘以b的绝对值; 等于a的绝对值乘b的绝对值; 这是标量的长度;

二、向量

1、基本操作

• 标量拓展到向量

• 标量就是一个数值; 向量就是刚刚提到的就是一行值; 可以既是行向量也是列向量; 但数学上并不太区分行和列;

• 这里a和b都是向量里面很多元素; c=a+b; 是说c的第 i个元素=a的第i个元素加上b的第i个元素;

• α是标量; b是向量的话那就α*b; 就是说; c的每一个元素等于α乘以bi; 如果做Sin的话也是每个元素做Sin;

• 向量的长度

• 就是向量的长度; 就是向量的每个元素的平方求和; 再开根号;

• 就说a的长度是大于等于0的;

• 两个向量的长度小于等于a的长度加上b的长度; 就是三角定比;

• a乘以b; 就是说它等于如果a是一个标量的话; 那么它等于a的绝对值乘以b的向量的长度;

2、空间表示

• 图示
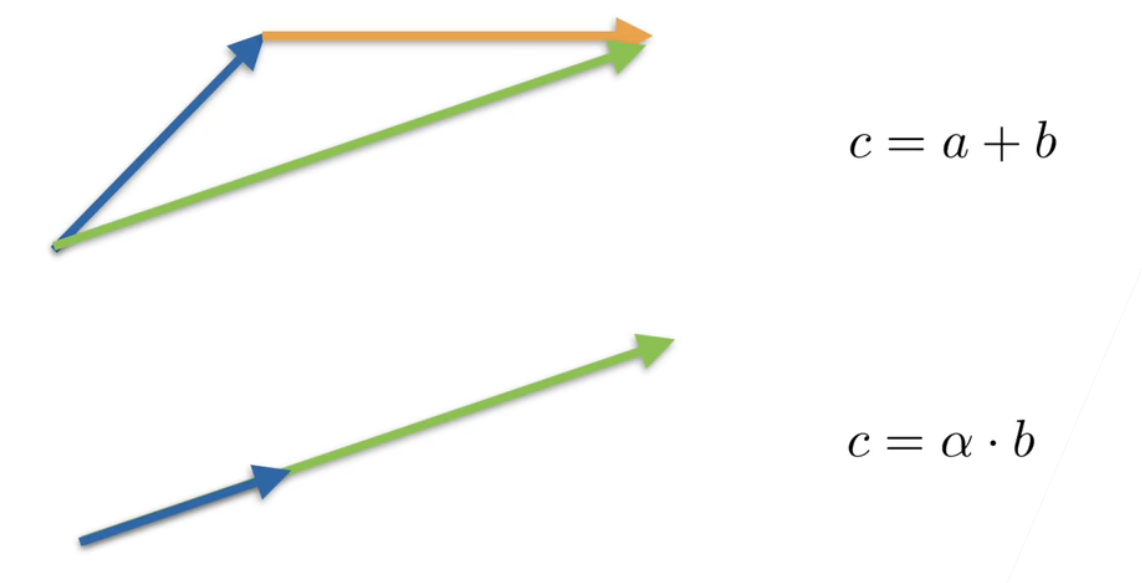
• 向量可以给一个直观上理解; 蓝色的是a的话; 黄色是b的话; a+b; 就是把这个两个向量接起来就是c; 就绿色c等于a加b;
• 如果a还是这个蓝色的；α是一个长度是个标量的话; 那就是说可以把它拉长;

3、乘法

• ====

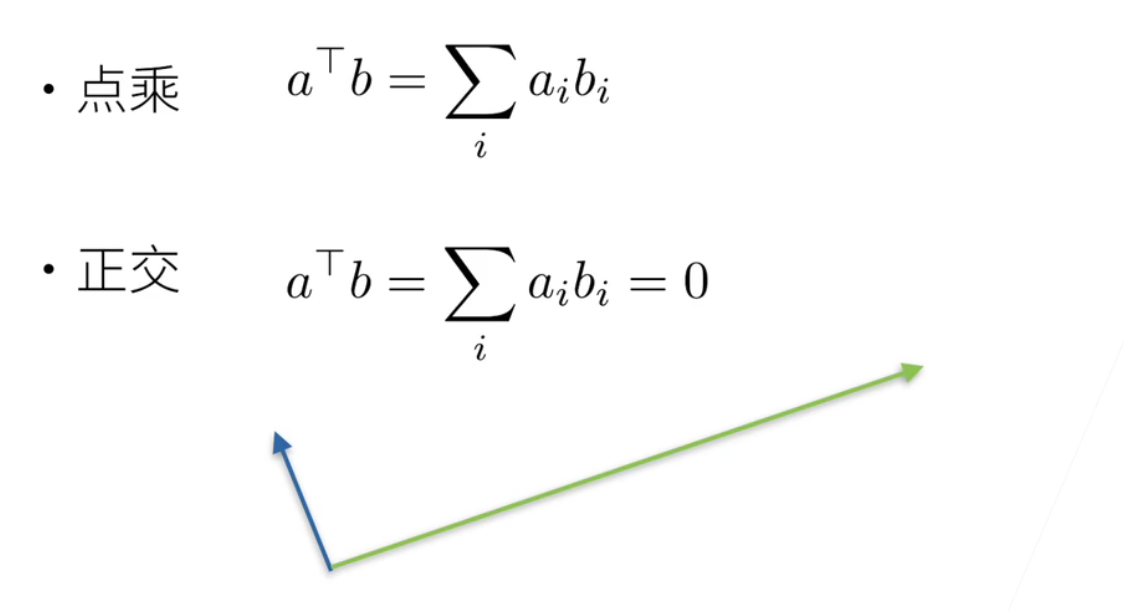
• 就a的转置*b就=把a的i元素乘以b的i的元素; 然后求和;

• 如果这两个向量是正交的话; 就是垂直的话; 那么他的求和是等于0的; 这是他这是正交向量

三、矩阵

1、基本操作

• 看到矩阵; 就说n行与n列

• c等于a加b; 那就是每个元素相加;

• α标量乘以矩阵那就每个元素相乘α;

• sin也是每个元素求sin; 这是一样的;

  
  

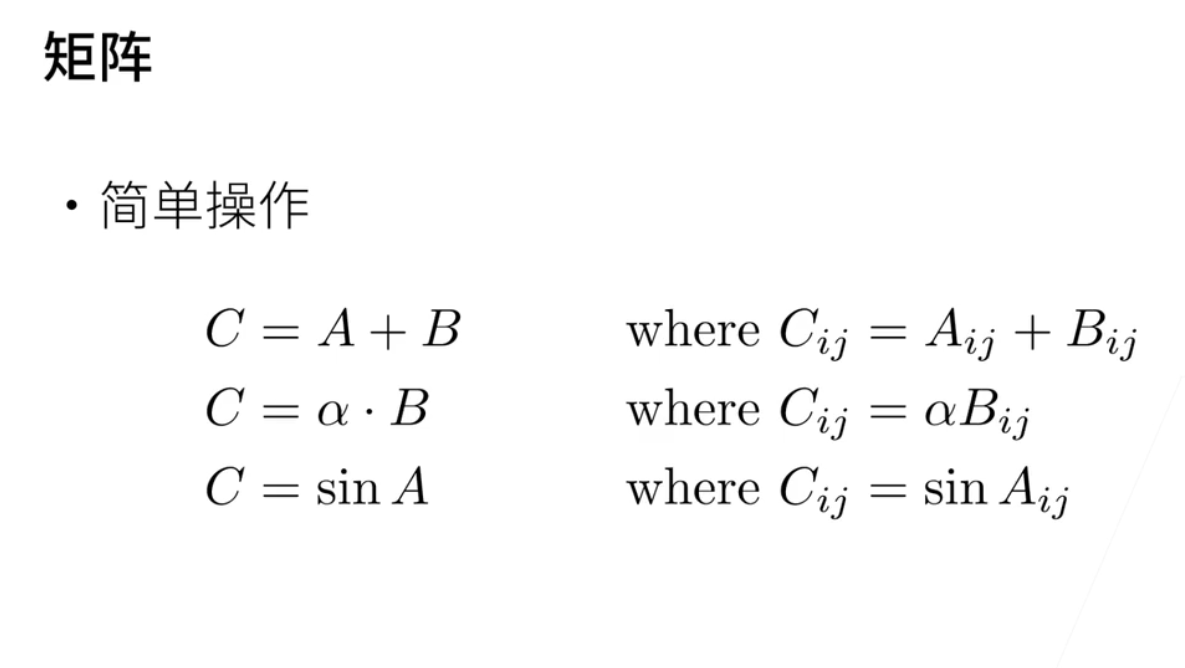
2、乘法

• 矩阵乘法略有不同
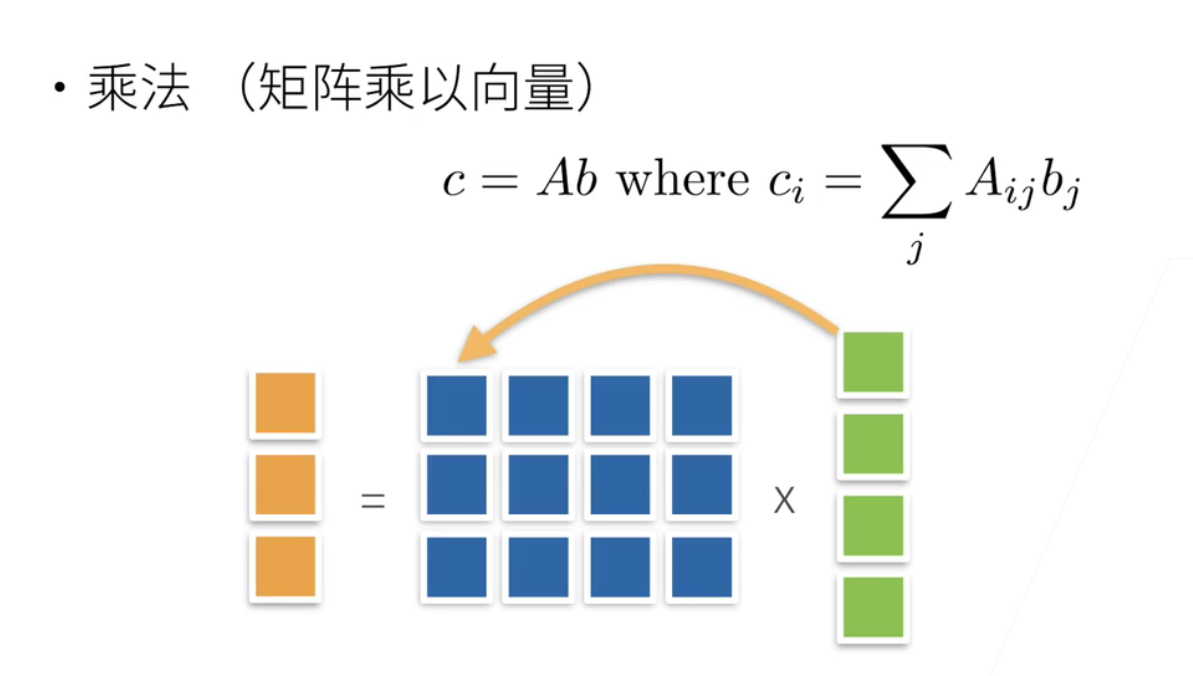
• 矩阵a乘以b就是a是一个矩阵; b是一个向量; 就是说对 a的每一行*b；做一个列向量; 就是每一行和这个列向量做内积;
• 就是每一个元素; 乘起来然后求和; 写到第一行; 这一行第二行再跟他列向量做内积; 写到第二行; 第三行跟列向量做内积写到第三行; 这是矩阵的乘法; 因为之后的机器学习所有的模型; 矩阵乘法是最基础的;

3、空间表示

• 矩阵乘法从直观上来说; 它是一个扭曲空间

• 可以认为是说一个向量; 通过一个矩阵乘法; 变成了另外一个向量;

• 就是这个矩阵; 其实是把一个空间进行了扭曲; 比如说这个是原始的两个向量; 通过矩阵乘法之后这个向量蓝向量变成这个蓝向量; 这个绿向量变成这个绿向量; 就说这个矩阵; 就是把整个空间进行到一个扭曲; 这是线形代数里面要讲的事情;

  
  

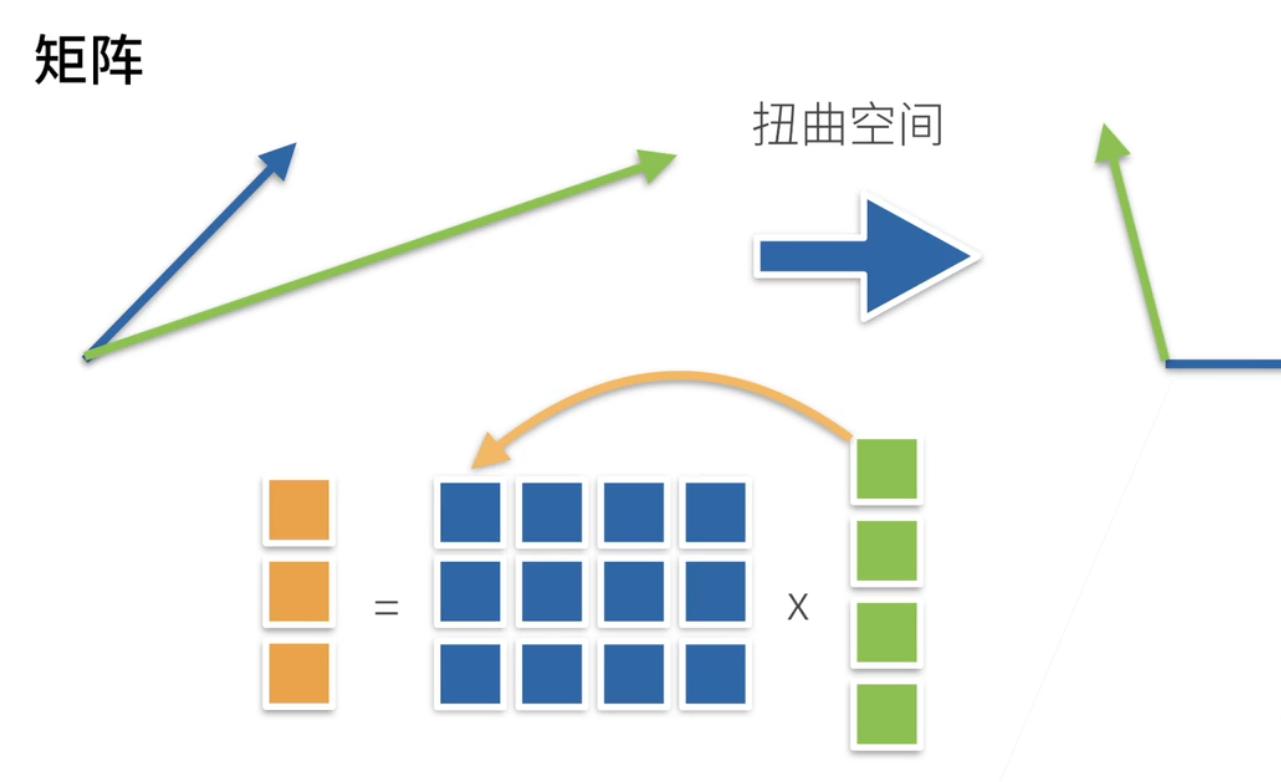
4、乘法

简单的矩阵乘法！

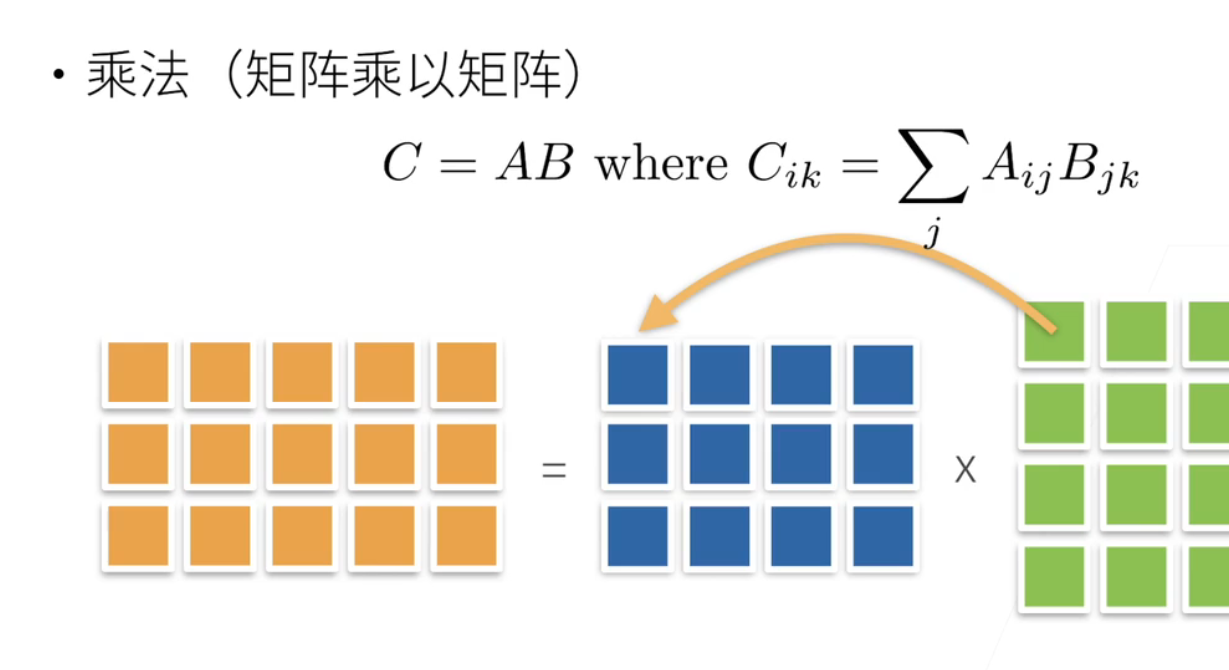
5、范数

• 矩阵范数
• [向量范数与矩阵范数](矩阵基础 | 向量范数与矩阵范数 - 知乎 (zhihu.com))
• 矩阵一样的; 要长度叫做范数; 因为c和b都是向量的话; 因为c等于a乘以b; c的长度就向量的长度; 根据刚刚的定义一定会小于等于a的范数乘以b的范数;
• 然后这个取决于怎么衡量b和c的长度了; 就说常见的范数有矩阵范数; 就说最小的满足上面公式的值; 就说对于a的矩阵;
• F范数的话; 把这个矩阵拉成一条向量; 然后做一个向量的范数；就说把a的所有的元素乘平方全部加起来; 然后开根号就是f范数; 因为它f范数比较简单; 所以一般会用f范数; 就矩阵范数会算起来会比较麻烦一点;

6、特殊矩阵

• ====
• 对称的; 和反对称; 就是说对称矩阵是以这条线; 它在这条线上; 是一个对称的; 就说这两个元素是一样的; 这两个绿色是元素的是一样的; 就是Aij等于Aji;
• 反对称就说Aij等于负的Aji;
• 另外一个说正定; 正定是说如果一个矩阵是正定的话; 那就是说它这个矩阵乘任何一个行 一个列向量和一个横向量; 它都大于等于0; 就是它是一个正定矩阵;

7、特征向量

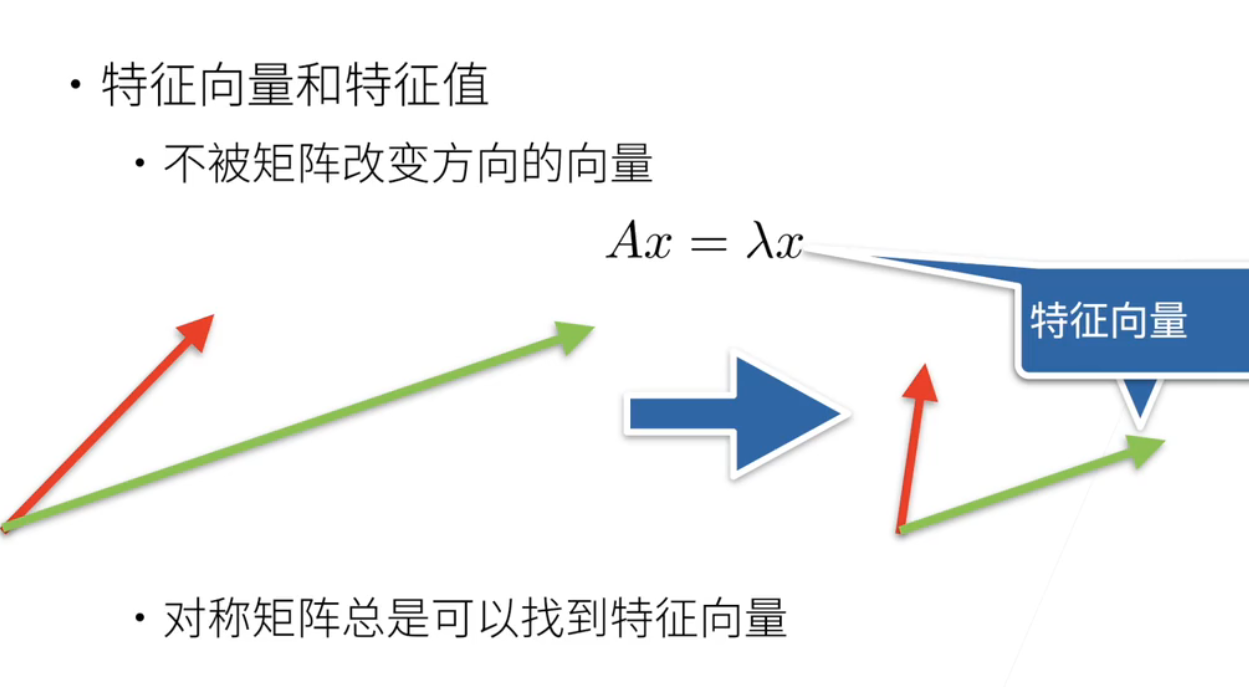
• 特征向量和特征值
• 特征向量; 是不被矩阵改变方向的向量; 矩阵就是把一个空间进行一个扭曲; 但有一些特殊的一些向量不被这个矩阵作用之后它不会改变;
• 这个红色和一个蓝色的向量; 被a作用之后; 做到这里; 红色被改变了; 但绿色没有被改变; 就绿色的方向没有变; 但是大小变了没关系; 那么这个绿色就是特征向量; 这个就是一个直观上的理解啊; 对称矩阵总是能找到特征向量; 但不是每个矩阵都有特征向量;

四、D2L注意点：

1、矩阵克隆

在这里使用克隆的话；更改B的数值并不会影响到A的数值；如果使用B = A；这样只是给的索引；

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
A, A + B

2、矩阵降维

关于2.3线性代数中的6降维需要重点理解；如何按照特定的轴做sum

举个例子；假设我们有个矩阵：5行4列；那么它的shape是[5,4]的list；它的维度就是2；并且它的axis：即它的轴；第一个轴是0；第二个轴是1；就是你的shape是一个list，那么第0轴就是第一个元素；2轴就是第二个元素；那么按照行就是轴为0；按照列就是轴为1；

如果按照axis=0来做sum的话，那么步骤就是按照第一列求sum；然后第二列求sum；以此类推得到的是一个长为4的行向量；

如果按照axis=1来做sum的话，同理；

如果是三维的话， shape[2,5,4] ；

如果按照axis=1来做sum的话，

五、QA

很多的东西啊~

No.3 矩阵计算

矩阵计算;其实是讲矩阵怎么求导数;因为对于机器学习;或者是说对于深度学习来讲;要知道怎么求导数;因为你的所有的优化模型的求解;都是通过求导数来进行的;

一、标量导数

• 高中数学标量的导数：y是一个函数;对函数y在x上求导

• a不是x函数的话;那么它对于x的导数;是0;

• 如果y是x的n次方的话;那么它的导数;那就是n乘以x的n减一次方;

• 如果y是x的指数的话;那么它的导数不变;

• 如果它是log的话;它会变成了x分之一;sin变成cos

  
  

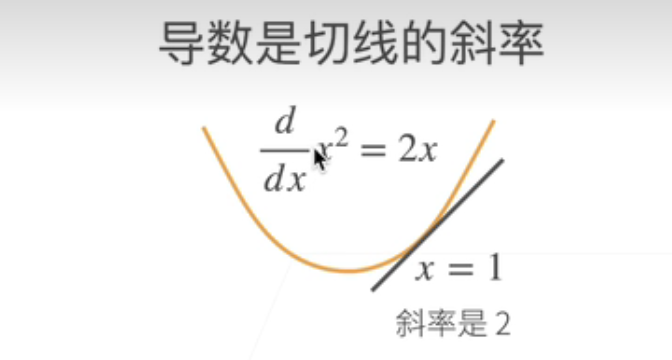
• 导数就是切线的斜率

• 比如说我有一个函数;y等于x的平方;那么画出来就是个黄线;那么这个它的导数那就是2 x;

• 然后在x等于1的导数;那么把x等于1代进去那么它就是2;那么在x等于1这个点;可以画一个切线;那么切线这个斜率它就是2;就是导数的意义;

  
  

• 导数的一些基本的运算规则

• 如果y是一个;u函数加上一个v函数的话;那么对x求导的话;那就是分别对u求导和对v求导;

• 如果y是u乘以v的话;那么就是说对u求导;然后乘以v加上对v求导乘以u;

• 对于y如果是一个u的函数;u是一个x的函数的话;那么y对x求导就是先对;y是u的函数先对u求到;然后对u对x求导;它可以做一个分解就是一个链式法则;

二、亚导数

• 不一定存在导数的话会怎么办将导数拓展到不可微的导数的情况下;怎么办？
• 举个简单例子;y是x的绝对值;那黄线就是这样子;在0点的时候它的切线不为1;就说你可以斜率等于0.5也行;等于-0.3也行;它都在这个线在这个函数的下面;
• 那么就是说;可以通过一个叫亚导数;就是它的数学符号就是一个；那就说x大于0的话它是一;x小于0的话它是-1;但是在x等于0的时候;它可以在-1和一之间取任意的值;

三、梯度

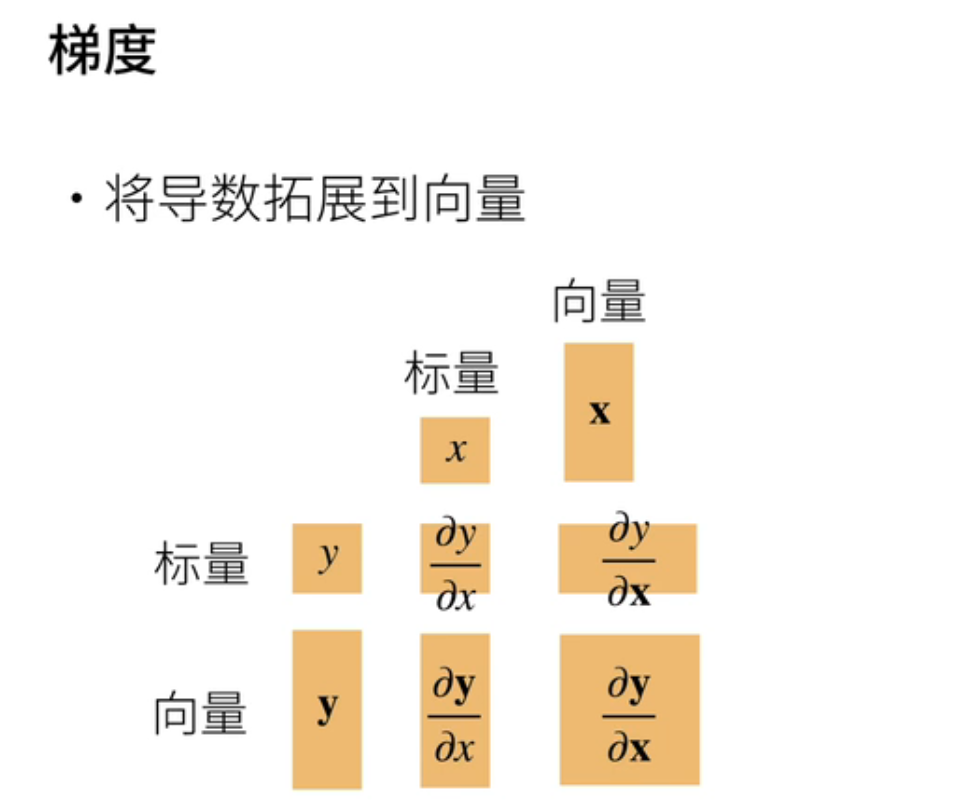
• 导数拓展到向量;通常我们叫梯度

• 就是说这里画了一张图;就是说最关键的是说要搞得清形状;当拓展到向量矩阵的时候;要把形状搞对；形状搞对了的话通常也就对了;

• 就是说当y是x的函数;y是标量;x是标量的话;它的求导当然是一个标量;

• 当你如果是y是一个向量;x是标量的话它会变成一个向量;同样的话你y是一个标量;你x是向量的话;它也是一个向量;那如果两个都是向量的话;它会变成一个矩阵;

  
  

1、y是标量，x是向量

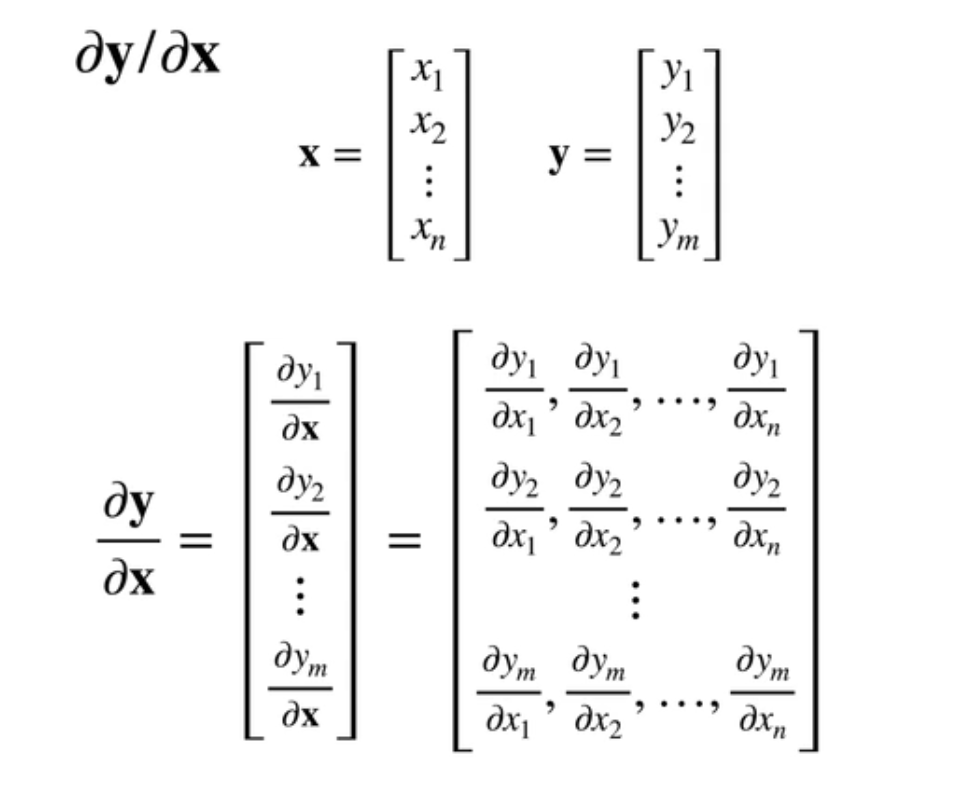
• y是一个标量;x是一个向量;

• X这是一个列向量;那么它的导数关于列向量的导数;它是一个行向量;

• 就是理解一下：就列会变行;它的第i个元素;那就是y是一个标量;关于x的第i个元素的导数;

• 举个例子;那就是说x是一个长为2的一个向量;y就是定义为第一个元素的平方加上2乘以第二个元素的平方;

• 那么就是说它的导数就是一个;首先我们第一个元素那就是说X1;它要求导那就是2乘X1;第二个元素就是对X2求导;那就是4倍乘X2;这就它的导数它是一个行向量;

  
  

• 理解

• 怎么理解这个东西呢;关键是一个理解;因为就是说可以不知道导数怎么求;但是一定要需要是怎么理解的;

• 理解上来说就是说;这个东西可以画成一个等高线;就是说这个函数X1的平方加上二乘以X2的平方;可以做等高线;就是一个一个这样子椭圆的形状;(好像是椭圆方程式)

• 那么对于X1和X2等于1和1这个点;我可以做等高线做切线;然后它的做一个正交方向出来;这个方向的值是一个2和4;它就跟你的梯度是一样的;你把X1和X2带值进去的话就变成2 4;就是说你的梯度就是跟你的等高线是正交的;

• 意味着是说你的梯度指向;是你的值变化最大的那个方向;这是一个核心的概念;就是说梯度一定指向你那一个值变化的最大的方向;通常是往大的直走;这个也是今后所有的机器学习求解的一个核心思想;

  
  

• 对上面的情况进行举例子

• 首先y是一个标量;x是一个向量;当标量是一个跟x无关的函数的话;那么它是一个全零的一个向量;它是一个行向量;就是我们要转置来表示;

• 如果是a乘以u的话;那么就是说你把a拿出来;然后对u对x求导;如果是求和的话;对x求和的话;那么就会变成一个全1的一个向量;

• 同样的话之前如果是u加v的话;那么同样的话;先对u就求导数和对v求导数;然后加起来;

• 乘法的话是一样;就是说;关于u关于x的导数乘以v加上v;关于x的导数;再乘以u;如何累计的话;首先是u的转置乘以它关于v的;关于x的导数就说两个向量;关于向量的导数它是一个矩阵;就是一个;行向量乘一个矩阵;再加上另外一个横向量乘一个矩阵;这就是一个;所以它的导数出来也是一个行向量;

  
  

2、y是向量，x是标量

• 上面的函数是一个向量;下面的是一个标量的话

• 假设y是一个列向量;那么关于列向量关于标量的导数;它也是一个列向量;就说刚刚是要会变现在是不变了;

• 所以可以看到这个图;所以是说当x是一个列向量;y是一个标量;那么它的导数是一个很怪的行向量;如果y是一个列向量;x是标量的话;那么它是一个跟它一样长的一个列向量;

• 所以说这个被称之为分子;分子布局符号你可以反过来;你可以把它就是说它们行列可以交换;那就叫分母布局;就说你有哪个布局的没关系;只是说你必须要用一个布局;这样子你的形状是能对上的;所以这里一般是用分子布局方法;

  
  

3、y和x均是向量

• 向量关于向量是一个矩阵

• 就是说;y是一个向量;x是一个向量;那么因为y是一个向量;先把它拆解成一个列的向量;然后每一列的那一个元素;第i个元素就是y的第i个元素;关于x的一个导数;它是一个横向量;那最后会变成一个矩阵;

  
  

• 上面的例子举例

• 同样的话;a是一个跟x无关的一个向量的话;那么它的输出是一个全0的一个向量;

• 不然的话如果是本身的话;那他就会变成一个对角;

• 如果是A乘以x的话;y等于x乘以x的话;它的导数是a这个矩限的本身;

• 如果你是反过来的话;你是一个x导啊转制成a的话;那么它导数就是a的转制的本身;这两个是非常有用的;之后可能会讲到的一个东西;然后同样的道理是说;如果是标量乘以u的话;那么呢就是标量可以拎出来;如果是矩阵乘以u的话;矩阵而且是跟x无关的话;那么可以把a拿出来;啊如果是u加上v的话;分别对u和对v求了;

  
  

4、y和x均是矩阵

这里基本不会；

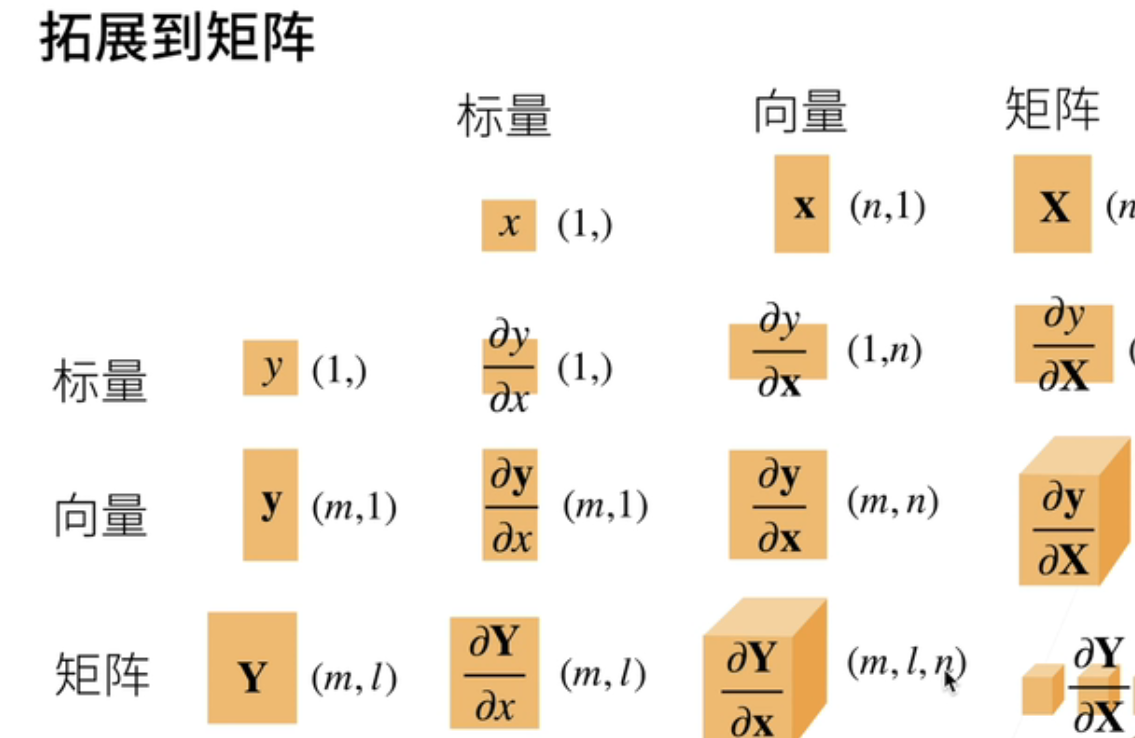
输入拓展到矩阵;就是大家不要求全部能弄懂是怎么回事啊;首先说我们当你的y是一个标量;这是一个矩阵的话;刚刚记得吗;我们如果是向量的话;我们就把它其实转置了一下;我们可以把一个通过一个刚刚提到过;可以通过用一个二维的数组来区分行向量和列向量;如果你的项量是在下面的话;那么它的结果会要转一下;如果你矩阵的话;你会被和k和n会转至一下;同样的话;如果你矩阵在上面的话;你其实不会变化的;就是m乘l是不会变化的;当这里比较好玩的是说;当你的y是一个矩阵;你x是一;个向量的话;那等于是说你要把n放到后面;然后拎到最后这个地方;如果你的y和x都是一个矩阵的话;那就是更好玩了;就是说我们绕开一点啊;就是说前面两项是来自于y的m乘以l;但是呢后面两项是来自于x;但是你要把x给翻过来;就是k要放到这里然后n要放到最后;它就会变成一个四维的一个丈量啊;就是说你当然可以做到更高位的情况;就是说以此类推;可以做到更高位的情况;这就是我们的矩阵的技巧;

四、QA

1、导数作用

导数的作用主要是进行梯度下降;但容易陷入局部最优解;请问是不是可以通过Leap PROF函数;或者其他方法来使得下降得到全局最优解;这个问题就是说;如果你是凸函数的话你可以拿到最优;如果你不是突函数的话;其实你不管用;几乎是拿不到最优解的;就说当然你可以;理论上你数学是可以但从计算上来说;几乎是拿不到最优解的;这个真的是;啊一个不幸的消息啊;

而且机器学习几乎是不会处理凸函数就是说;如果你这个问题能得到最优解的话;那就是一个P的问题;我们机器学习不关心P问题;我们只关心NP的问题;所以大家不要去纠结最优解这个事情;

2、自动微分和计算图

pytorch和M开头的;采用的是自动微分和计算图;对的;我们马上就会讲自动微分和计算图;就说不会让你自己去求导;大家能够知道;导数大概是怎么算的;至少你的形状能够搞清楚;就说你必须要知道整个是怎么算出来的;但是你能大概理解导数的形状跟你的input的形状是;什么样一个变化的关系;我觉得这个比较重要;

No.4 自动求导

一、向量链式法则

• 标量的链式法则

• y是一个u的一个函数；u是关于x的一个函数；那么y对x求导的话；那就是说先把y；把u做成一个变量进来求导；

• 然后把u做成一个函数关于x的导数；要拓展到向量；最大的问题说要把形状搞对；就说y是一个标量；x是一个向量；那么首先u也是一个标量；这个当然是个标量；u关于x；它就是一个1乘以n的一个东西；那么1乘它就变成1乘n；就是这个形状不发生变化；

• 那假设u是一个向量那怎么办呢；那就y关于u；那还是一个一乘k；假设u是一个k尾的一个向量；那是一乘k；u关于x它是一个k乘n的一个矩阵；那么它一乘还会变成一乘n；然后你的y是一个向量；x是一个向量u也是一个向量；

• 同样的道理；假设你的是一个m乘n的话；那么它就是u是一个长为k的话；那么它是一个m乘k；然后它是一个k乘n这样子矩阵；两个矩阵一乘；它还是变成一个m乘n的一个矩阵

  
  

• 举两个例子

• 这就是一个之后线性回归的一个例子；首先；假设x和w它都是一个长n的向量；y是一个标量；那么函数z是说x和w做内积；减去y然后做平方；

• 要计算z关于w的一个导数；那我们怎么做呢；就是先分解吧；先把它写开；首先说我记一个a中间变量a；它是x和w的内积；b是a减去y；然后z是等于b的平方；这样子我们把它分解成三个步骤；然后我们用链式法则；

• 那z关于w的导数那就是说；z关于b的导数；b关于a的导数a关于w的导数；然后把这个z b a的定义展开；那就b的平方关于b；a减y关于a；x和w的内积关于w；那么第一项我们知道就是2b对吧；那么这一块就是因为它是一个；就是一；它就是x的转置；那么再把b的定义拆开；就b是怎么定义的；然后它长成这个样子；

• 那么就会得到说z关于w的导数；那就是；w和x的内积减去y然后乘以x的转置；这是一个标量；所以它是说因为它是一个；它的向量在下面；所以它出来的是一个转置的一个向量；

  
  

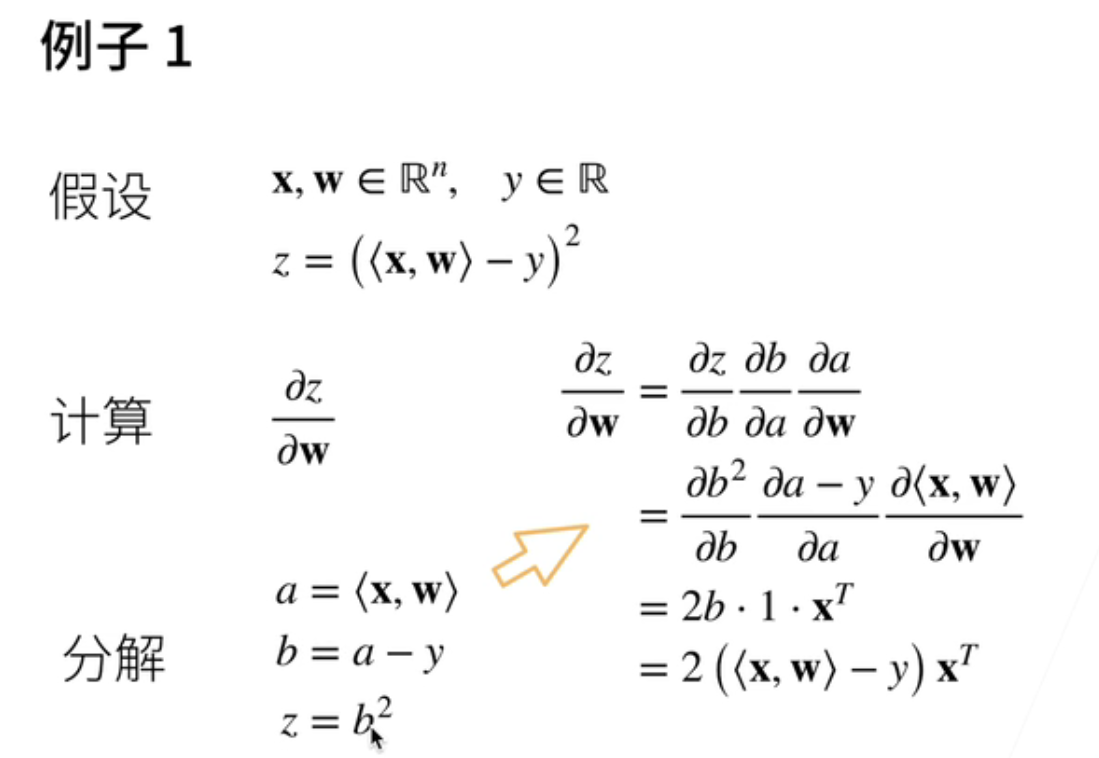
• 涉及到矩阵了

• x是一个m乘以n的一个矩阵；乘以w；一个向量减去另外一个向量；同样的道理它是一个标量对吧；

• 所以我要对标量对于向量求导；其实这个跟之前是一样的；首先就运用中间变量；a是一个向量等于x乘以w；b等于a减去y；z就等于b的||；用这个展开；那么就说它的本身是一个2的；b的转质；乘以它是一个ident；那就是说一个identity Matrix；它就是x的本身；那么最后的把b展开的话那就是；x乘以w减去y的转值乘以x然后乘2；

  
  

二、自动求导

• 目前，我们有能力执行自动求导。如果你提供一个函数，我可以使用链式法则和基本的导数规则，将其展开为一个导数链。然而，最大的问题在于，神经网络通常包含数百层，手动进行导数计算几乎是不可行的。因此，我们需要自动求导的能力，即在指定点计算函数的导数。
• 自动求导实际上有两种不同的定义：符号求导和数值求导。符号求导可以在给定一个函数时，明确地计算出其导数。如果你曾使用过类似Mathematica的软件，你可能已经体验过这种功能。另一种方法是数值求导，它允许我们在不知道函数的具体形式的情况下，通过数值逼近来计算导数。这可以通过微小的变化h来实现，即通过计算 (f(x+h) - f(x)) / h 来逼近导数值。
• 现在，让我们来掆自动求导是如何实现的。这涉及到一个称为计算图的概念。虽然我们在使用PyTorch等深度学习框架时不需要深入理解计算图的内部工作原理，但了解计算图的概念对于理解自动求导的基本原理是有帮助的。如果你之前使用过TensorFlow或其他深度学习框架，你可能已经对计算图有所了解。

三、计算图

• 关于计算图，实际上本质上是链式法则的一个求导过程。首先，我们将代码拆分成操作子，逐步展开。然后，我们将计算表示成一个无环图。让我们继续使用之前的示例，其中z等于x与w的内积减去y，然后再求平方。我们按照类似的方法，引入两个中间变量a和b，将每一步的计算都表示为基本的计算单元。因此，每个节点表示一个操作，也可以表示一个输入值。
• 例如，一个节点表示w，另一个节点表示x，还有一个节点表示a，它在这里执行计算。将a和y输入后，我们得到b。最后，将b输入后得到z。这就是计算图的构建过程，它是一个无环图的表示。

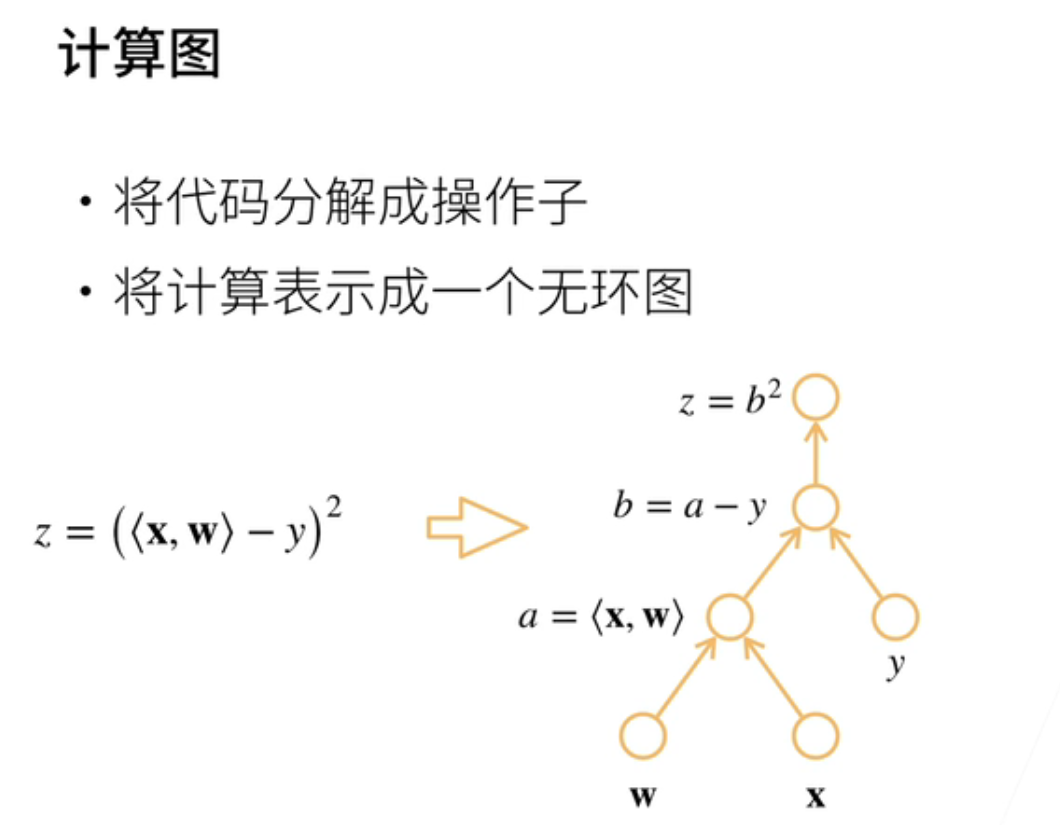
这个~~~

四、自动求导的两种模式

• 有两种自动求导的方法。让我们再回顾一下链式法则。假设我有一个函数y，它是关于x的函数。在计算整个导数过程时，我有两种方法：一种是正向计算，另一种是反向计算。
• 正向计算意味着我从x开始，首先计算关于x的导数U1，然后计算关于X1的导数U2，然后将它们相乘，一直向下传递，直到最后计算出目标导数。
• 反向计算是另一种方法。在这种方法中，首先计算y作为最终函数关于中间变量的导数，然后乘以倒数第二个中间变量的导数，依此类推，一直向前计算，直到最前面的导数。这个方法也被称为反向传播。
• 自动求导是计算机科学领域一个历史悠久的领域，它在人工智能中占有重要地位。其中一个著名的方法叫做反向传播。

五、反向累积

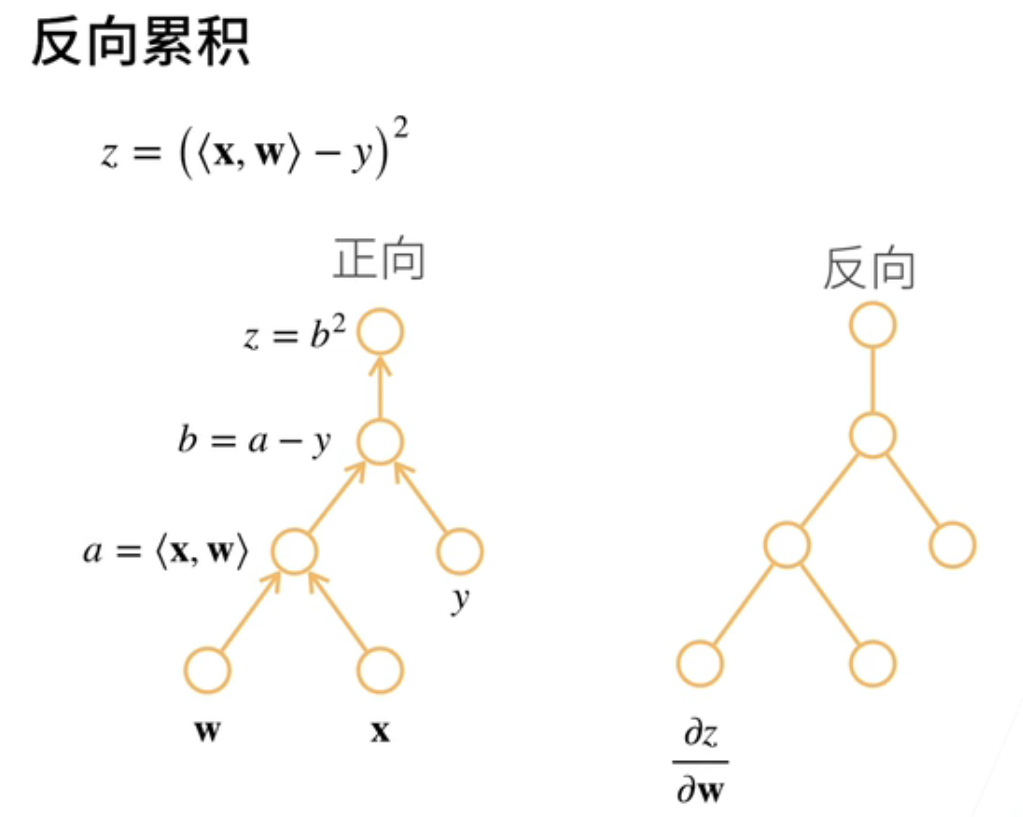
• 那么，反向传播究竟是如何计算的呢？首先，我们先回顾正向传播，因为我们已经讨论了正向传播的过程。现在，让我们来看看反向传播。
• 在反向传播中，我们首先计算z关于b的导数。这个导数等于2乘以b，根据之前的计算结果得到。因此，我们需要在计算z关于b的导数时，访问之前计算的b的值，将其存储在某个地方，然后将其检索出来。我们需要访问之前的计算结果。
• 同样地，我们可以计算z关于a的导数，这个导数也依赖于之前的计算结果。最后，我们计算z关于w的导数，这需要知道w的值和a的值，所以我们需要同时知道这两个值。因此，在反向传播中，我们需要存储所有中间计算的值，以便在反向计算时使用。
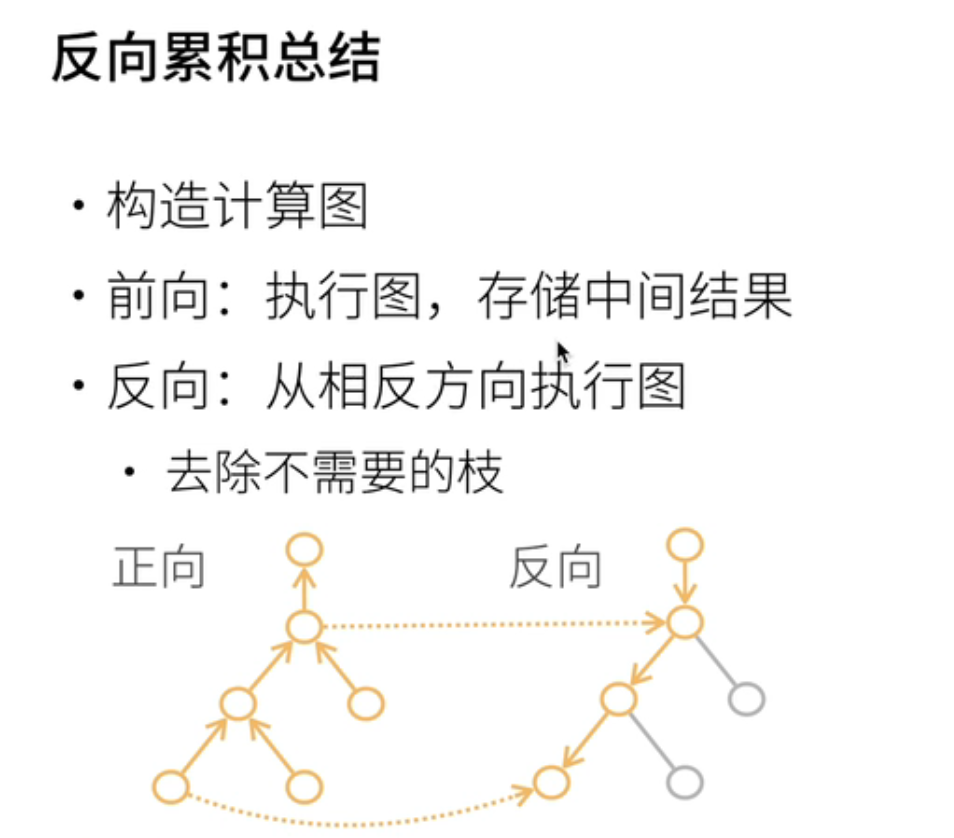
• 反向传播是一种累积的过程，与正向计算相反。在正向计算时，我们需要将所有中间计算的值存储下来。但在反向传播时，我们按相反的方向进行计算，如果某些导数不需要的话，我们可以选择不计算它们，但是我们需要保留中间结果，以便在后续的计算中使用。

• 那么，让我们来讨论一下计算复杂度。假设我有n个操作子，比如我的神经网络有n层。在正向传播和反向传播中，实际上代价差不多，即你需要运行正向传播和反向传播一次。换句话说，对于神经网络的前向传播和后向传播，计算复杂度是相近的。
• 然而，更加重要的是内存复杂度。它是O(n)，这意味着你需要存储所有的中间计算结果。这对于深度神经网络来说需要大量的GPU资源，因为在求梯度的过程中，需要保留前面的计算结果。
• 另一个值得注意的概念是正向累积。正向累积的好处在于内存复杂度是O(n)，无论网络有多深，都无需存储任何结果。然而，它的问题在于，计算一个梯度需要遍历整个网络两次。因此，正向累积通常在神经网络中不被使用，因为它的计算复杂度太高。

六、D2L注意点

1、梯度存储问题

在计算梯度之前，需要一个地方来存储梯度，

x.requires_grad_(True)  # 等价于x=torch.arange(4.0,requires_grad=True)
x.grad  #通过这个就可以以后访问梯度了；即y关于x的导数是放在了这个地方的；

2、求导问题

其实深度学习中大部分y都是标量；即之前学的向量对向量的求导在深度学习中是用的很少的

七、QA