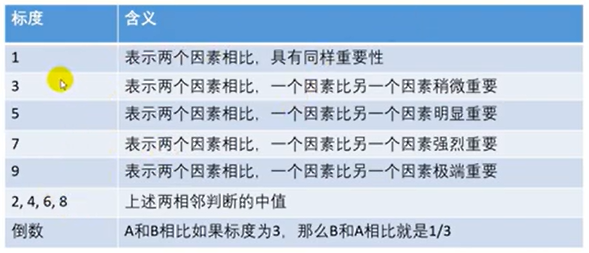
主要来解决评价类问题

什么是评价类问题：选择哪种方案最好，哪位运动员表现的更优秀。

评价类问题可以用打分解决

同一颜色的单元格权重之和为1

解决评价类问题，大家首先要想到以下三个问题：

1.我们评价的目标是什么？

2.我们为了达到这个目标有哪几种可选的方案？

3.评价的准则或者说指标是什么？（我们根据什么东西来评价好坏）

一般前两个问题是显而易见的，第三问题的答案需要我们根据题目的背景材料、常识以及网上搜集到（知网，万方、谷歌学术等）的参考资料进行结合，从中筛选出最合适的指标。

分而治之的思想： 来确定指标的权重来填表

问题：一次性考虑这五个指标的关系，往往考虑不周

解决方法：两个两个指标进行比较，最终根据两两比较的结果来推算出权重

层次分析法的思想登场：

正互反矩阵：若矩阵中每个元素都大于0且满足aij*aji=1即层次分析法的判断矩阵

一致矩阵：若正反矩阵满足aik=aijxajk

特点：各行（各列）之间成倍数关系

注意：在使用判断矩阵求权重之前，必须对其进行一致性检验

一致性检验原理：检验我们构造的判断矩阵和一致矩阵是否有太大的差别

引理：n阶正互反矩阵A为一致矩阵时当且仅当最大特征值=n.且当正互反矩阵非一致时，一定满足最大特征值大于n。

一致性检验的步骤：

第一步：计算一致性指标CI CI=(最大特征值-n)/(n-1)

第二步：查找对应的平均随机一致性指标RI

第三步：计算一致性比例CR CR=CI/RI 如果CR<0.1,则可以认为判断矩阵的一致性可以接受；否则需要对判断矩阵进行修正（往一致矩阵上去调整 两行成倍数）。

第四步：计算各层元素对系统目标的合成权重，并进行排序。

（1）RI怎么计算来的？

用随机方法构造500个样本矩阵；随机地从1-9及其倒数中抽取数字构造正互反矩阵，求得最大特征根的平均值，并定义 RI=（最大特征根的平均值-n）/(n-1)

一致矩阵怎么计算权重

判断矩阵计算权重：求出每一列的权重，再求各样本的平均权重

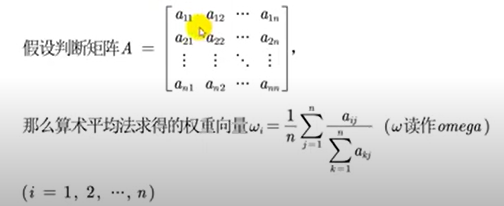
方法一：算数平均法求权重（可将文字叙述加到论文中）

第一步：将判断矩阵按照列归一化（每一个元素除以其所在列的和）

第二步：将归一化的各列相加（按行求和）

第三步：将相加得到的向量中每个元素除以n即可得到权重向量

方法二：几何平均法求权重

第一步：将A的元素按照行相乘得到一个新的列向量

第二步：将新的向量的每个分量开n次方

第三步：对该列向量进行归一化即可得到权重向量

方法三：特征值法求权重

一致矩阵有一个特征值为n，其余特征值为0.

假如判断矩阵一致性可以接受，那么我们可以仿照一致矩阵权重的求法。

第一步：求出矩阵A的最大特征值以及其对应的特征向量

第二步：对求出的特征向量进行归一化即可得到我们的权重

Excel F4可以锁定单元格

层次分析法第一步：

1.分析系统中各因素之间的关系，建立系统的递阶层次结构

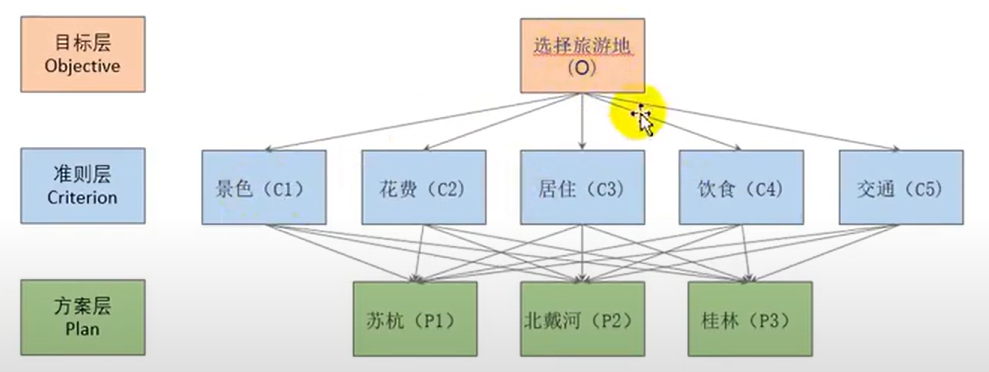
可将层次结构图加在论文中，可使用SmartArt生成，

或用亿图图示

层次分析法第二步：

2.对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较，构造两两比较矩阵（判断矩阵）

任何评价类模型都具有主观性：

理想：采用专家群体判断 现实：几乎都是自己填的

层次分析法第三步：

3.由判断矩阵计算被比较元素对于该准则的相对权重，并进行一致性检验（检验通过权重才能用）

三种方法计算权重：

（1）算数平均法 （2）几何平均法 （3）特征值法

建议大家比赛是三种方法都使用

层次分析法的一些局限性：

1.评价的决策层不能太多，太多的话n会很大，判断矩阵和一致矩阵差异可能会很大。

2.如果决策层中指标的数据是已知的，那么我们如何利用这些数据来使得评价更加准确呢

分享：

“我知道你最近很累 是那种看不见的 身体上的 精神上的 人际关系上的 面对未来和过去的那种无力感 但一定不要停下来 再坚持一下 如果觉得很累 就给自己买束花吧 生活是自己的 始终都要爱自己”