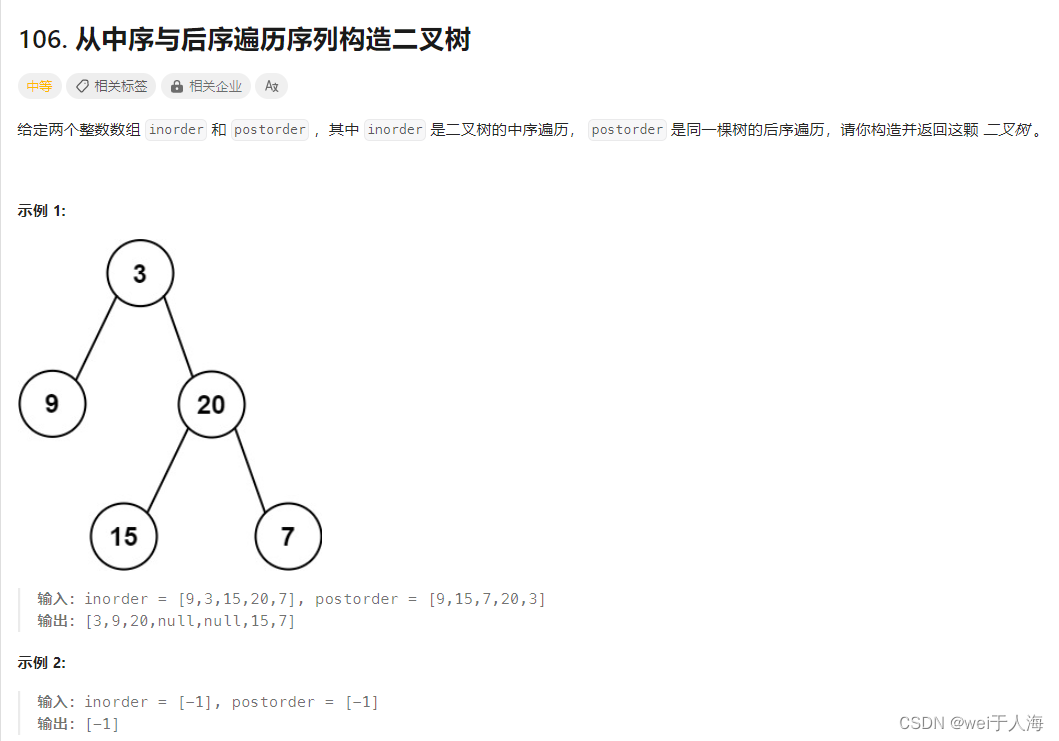
注意：该解法是基于二叉树中的值不存在重复所写的。

代码如下，可开袋即食

class Solution {
    private Map<Integer,Integer> map;
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        map = new HashMap<>();
        for(int i = 0; i < inorder.length; i++){
            map.put(inorder[i], i);//记录中序遍历的根节点位置
        }
        return build(inorder, postorder, 0, inorder.length-1, 0, inorder.length- 1);
    }
    
    public TreeNode build(int[] inorder, int[] postorder, int i_left, int i_right, int p_left, int p_right){
        if(p_left > p_right) return null;
        int r_root = map.get(postorder[p_right]);//中序遍历根节点位置
        TreeNode root = new TreeNode(postorder[p_right]);//创建根节点
        root.left = build(inorder, postorder, i_left, r_root-1, p_left, p_left +r_root-i_left-1);
        root.right = build(inorder, postorder, r_root+1, i_right, p_left + r_root-i_left, p_right-1);
        return root;
    }
}

这里主要的问题就是递归的边界问题了。

i_left：中序遍历的左边界

i_right：中序遍历的右边界

p_left：后序遍历的左边界

p_rigjt：后序遍历的右边界

递归的时候，需要注意里面的边界问题。

在左子树递归的时候，难的是后序遍历的边界处理。

i_left不变，i_right自然就变成r_root-1了

p_left不变，而p_right即左子树的长度了，即p_left+root-1-i_left。

为什么是这样算的？因为后序遍历的结果，前面一部分是左子树，后面一部分是柚子树，最后是根节点，如果不懂的话，可以自己画图，然后把中序和后序写出来，自己去想我这句话说的是什么意思。

然后右子树递归的时候，同样，难的是后序遍历的边界处理。

i_left变成r_root+1,i_right不变

p_left变成p_left+r_root-i_left，r_right向左移动一位，p_right-1

后序遍历的左右边界是这一题的难点。