文章目录
- 考试时间及策略
- 考试结果
- 考试反思
- 题解
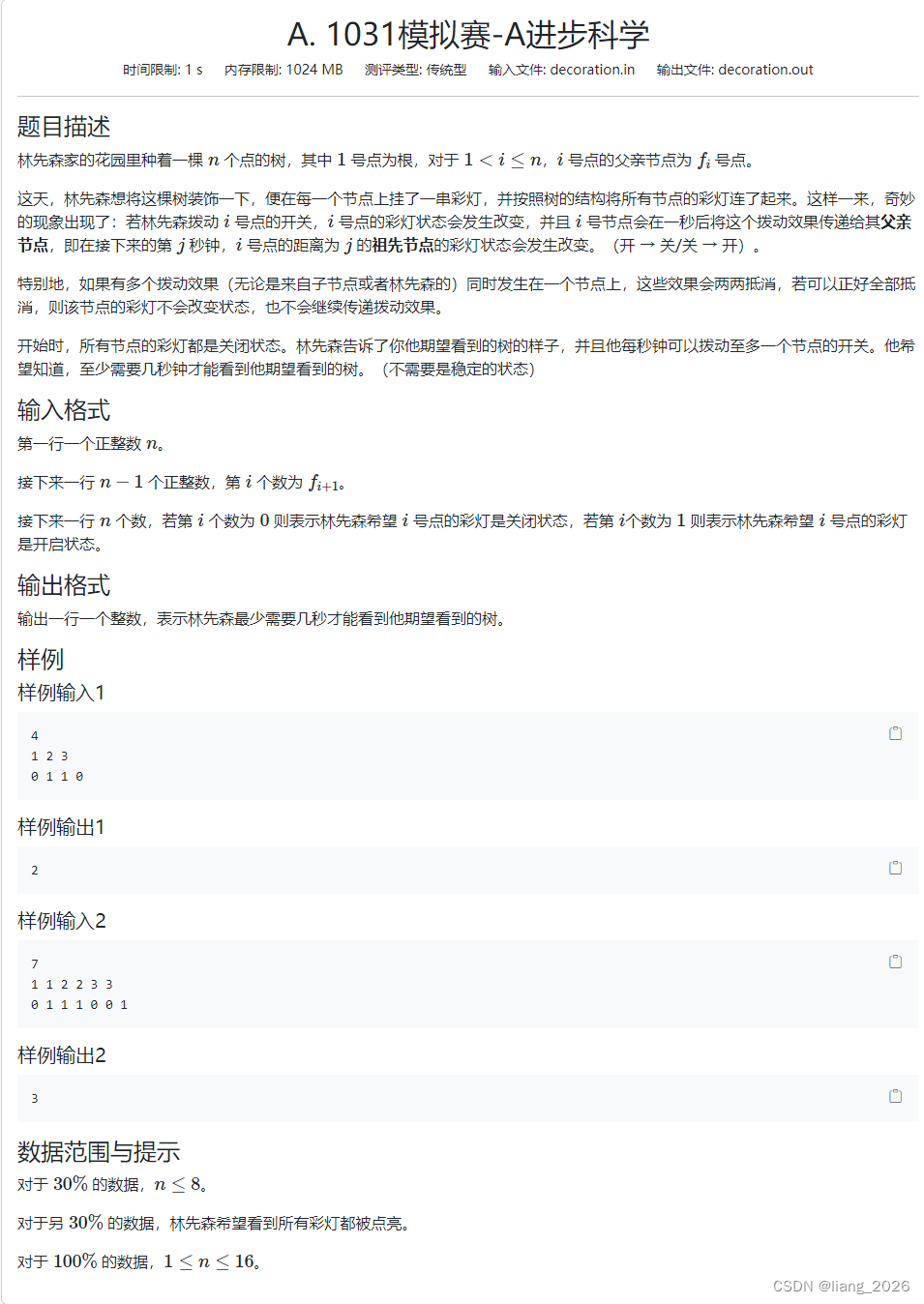
- A.进步科学
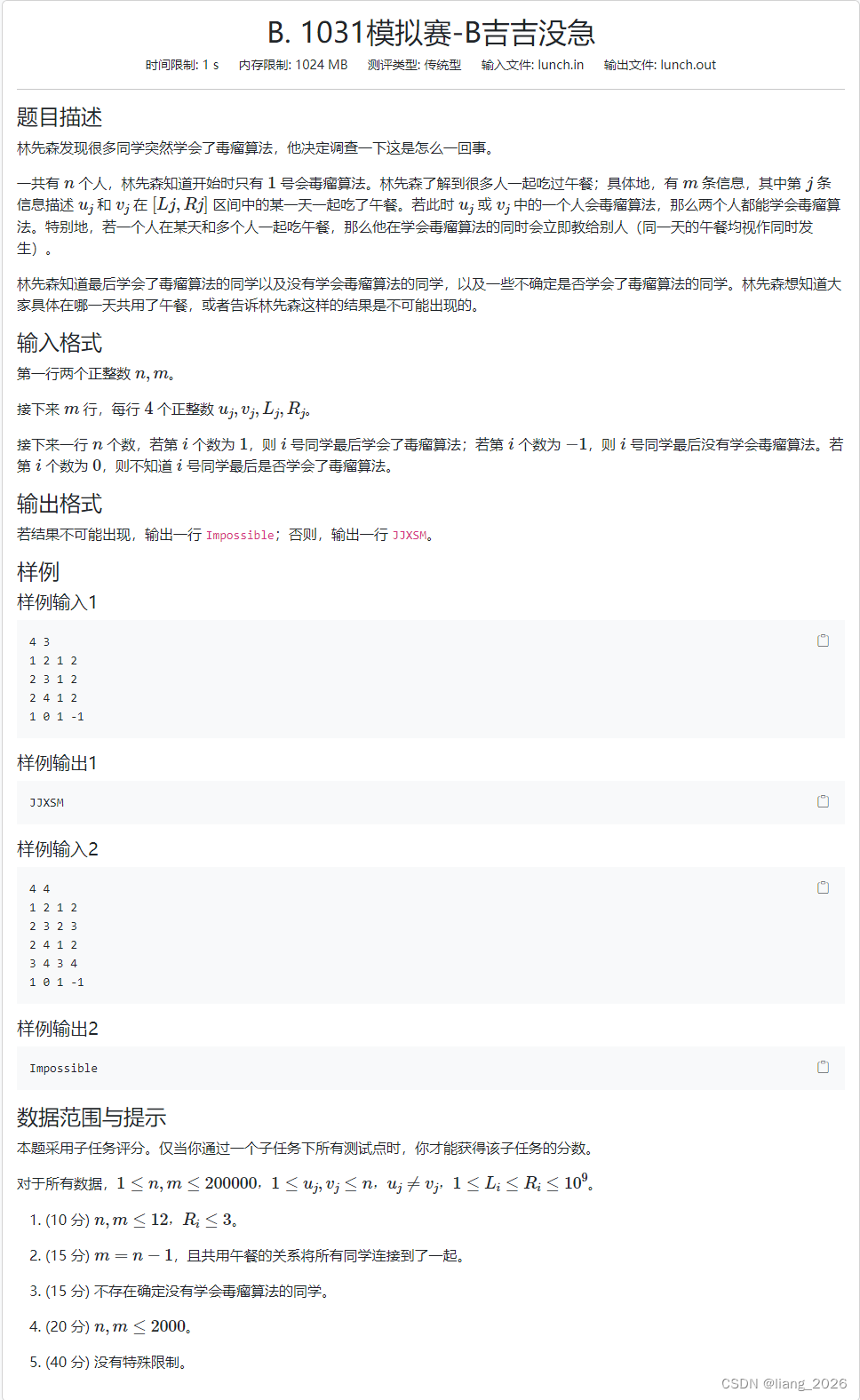
- B.吉吉没急
- C.老杰克哒
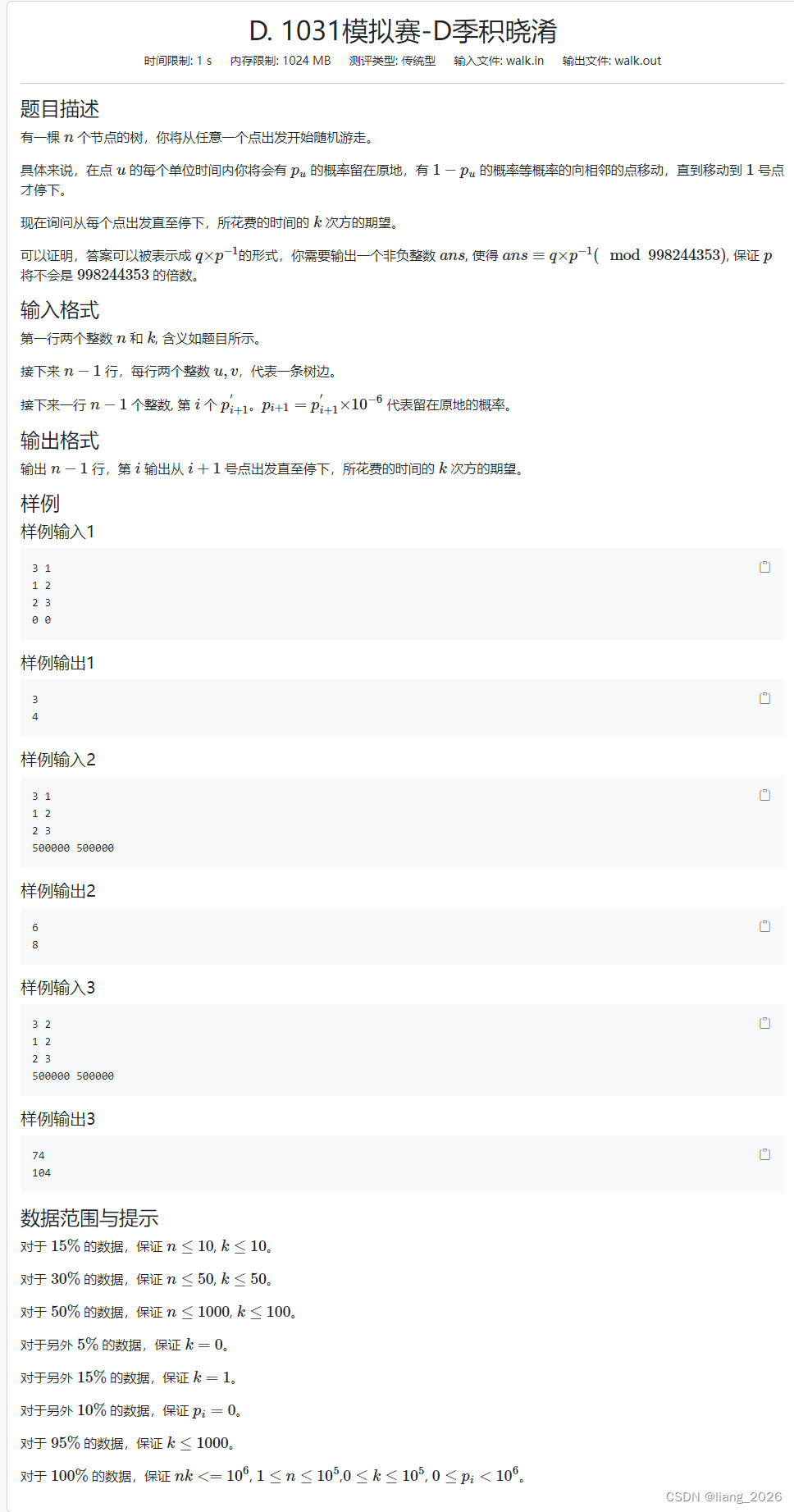
- D.季积晓淆
考试时间及策略
没啥好说的,因为好像都不会。所以全场感觉都在罚坐,很痛苦。
考试结果
30 + 0 + 50 + 5 = 85
考试反思
T1:T1是个神奇状压,感觉确实想不到。还是记住这个技巧吧。
T2:也是一道很难的题,会不了一点。
T3:只会 50pts 贪心的,没想出来暴力DP。如果能想出来暴力DP应该能想到正解吧。
T4:好像是FTT,会不了一点。
题解
A.进步科学
分析:
正常状压感觉没有什么阶段,我们设
d
p
i
,
m
a
s
k
dp_{i,mask}
dpi,mask 表示第
i
i
i 秒所有树上的节点的状态为
m
a
s
k
mask
mask 是否可行。
然后转移我们考虑若
d
p
i
,
m
a
s
k
=
1
dp_{i, mask} = 1
dpi,mask=1,那么我们让导致这个状态的操作整体后移1s,并且枚举第一秒操作哪个节点或者不操作节点。这样的好处是第
i
+
1
i + 1
i+1 秒 可以直接继承第
i
i
i 秒的状态,不用再考虑前
i
i
i 秒的操作会不会在 第
i
+
1
i + 1
i+1 秒产生影响。
我们设
j
u
m
p
i
,
j
jump_{i, j}
jumpi,j 表示如果扭动了第
i
i
i 个点,在扭动
j
j
j 秒后每个点的状态(最开始都是
0
0
0)。我们可以预处理出来
j
u
m
p
jump
jump 数组,然后转移 就是如果第一秒扭动了点
u
u
u,那么
d
p
i
,
m
a
s
k
→
d
p
i
+
1
,
m
a
s
k
⊕
j
u
m
p
u
,
i
dp_{i, mask} \to dp_{i+1, mask \oplus jump_{u, i} }
dpi,mask→dpi+1,mask⊕jumpu,i。最后如果某一时刻询问的状态为
1
1
1 就直接输出就好了。可以想到最多
n
n
n 秒就一定能得到答案。
CODE:
#include<bits/stdc++.h>// 设dp[i][mask] 表示i时刻状态为mask是否可行
using namespace std;// 我们考虑 i -> i + 1 的时候, 把操作往后平移一个单位,然后在第一时刻操作一个数。
const int N = 17;
bool dp[N][1 << 16];
int jump[N][N], fa[N], n, k, mask;
int main(){
freopen("decoration.in", "r", stdin);
freopen("decoration.out", "w", stdout);
scanf("%d", &n);
for(int i = 2; i <= n; i++){
scanf("%d", &fa[i]);
}
for(int i = 1; i <= n; i++){
scanf("%d", &k);
if(k) mask |= (1 << (i - 1));
}
for(int i = 1; i <= n; i++){
int now = i; k = 0;
jump[i][0] = (1 << (i - 1));
for(int j = 1; j <= n; j++){
if(fa[now]) jump[i][j] = (jump[i][j - 1] | (1 << (fa[now] - 1))), now = fa[now];
else jump[i][j] = jump[i][j - 1];
}
}
dp[0][0] = 1;
for(int i = 0; i <= n; i++){//最多n秒就可以了
for(int j = 0; j < (1 << n); j++){
if(dp[i][j]){
dp[i + 1][j] |= dp[i][j];//第一秒啥也不干
for(int k = 1; k <= n; k++){
dp[i + 1][j ^ jump[k][i]] |= dp[i][j]; // 第一秒选择了k,剩下的平移,那么可以抵消
}
}
}
if(dp[i][mask]){
printf("%d\n", i);
break;
}
}
return 0;
}
B.吉吉没急
分析:
很神奇的一道题。
我们首先把最后确定没学会算法的人当成一个限制。也就是说,我们考虑通过这些人来给其他人加一个限制。
具体来说,我们设
h
i
h_{i}
hi 表示每个人 允许最早在什么时间学会算法。如果
x
x
x 最后没有学会,那么
h
i
=
I
N
F
h_i = INF
hi=INF。我们跑一边 dijkstra ,设当前在堆头的点编号为
u
u
u,与它连边的点是
v
v
v,边的出现时间范围时
[
l
,
r
]
[l,r]
[l,r]。若
h
u
>
r
h_u > r
hu>r,说明如果
v
v
v 这个人想要学会算法,最早得在
l
+
1
l + 1
l+1 时刻,因为我们至少要拿出
1
s
1s
1s 使得这个时刻
v
v
v 还没学会算法,
u
u
u 此时和他吃饭。而
l
+
1
l + 1
l+1 相当与是这个限制的极限。我们将
h
v
h_v
hv 赋值成
m
a
x
(
h
v
,
l
+
1
)
max(h_v, l + 1)
max(hv,l+1),如果更新了放入堆中。如果
h
u
≤
r
h_u \leq r
hu≤r,也就意味着
h
u
h_u
hu 允许在
r
r
r 之前学会算法,所以
h
v
h_v
hv 什么时候学会都无所谓,我们只需要让边在某一个合适的时刻出现就好了。
跑完一边 dijkstra 后,我们检验一下
h
1
h_1
h1 是否大于
0
0
0。如果
h
1
h_1
h1 大于
0
0
0,那么一定无解,因为这意味着
1
1
1 号点不允许一开始就学会算法,与条件是冲突的。
否则,我们设
d
i
d_i
di 表示每个点在满足
h
i
h_i
hi 的限制下(也就是
d
i
d_{i}
di 要大于等于
h
i
h_i
hi)最早能够什么时候学会算法。因为每一个点越早学会算法,才越有可能教会其他最后确定学会的人。开始时
d
1
=
0
d_1 = 0
d1=0,其他的点设成
I
N
F
INF
INF,最后我们只需要检验所有确定学会的人
x
x
x 他的
d
x
d_x
dx 是否等于
I
N
F
INF
INF 就好了。如果有一个等于,那么无解,否则有解。
相当于
h
h
h 数组用来检验能否满足让确定学不会的人能够学不会,
d
d
d 数组用来保证确定学会的人可以学会。
CODE:
#include<bits/stdc++.h>// 首先根据不能学会算法的人求出每一个人学会算法的最早时间
using namespace std;// 然后在大于等于这个最早时间的前提下,每个人学会算法的时间应该尽可能早,这样能保证传递给后面的人
const int N = 2e5 + 10;
int read(){
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){if(c == '-') f = -1, c = getchar();}
while(isdigit(c)){x = (x << 1) + (x << 3) + (c ^ 48); c = getchar();}
return x * f;
}
struct edge{
int v, last, l, r;
}E[N * 2];
struct state1{
int x, val;
bool operator < (const state1 &a)const{
return a.val > val;
}
};
struct state2{
int x, val;
bool operator < (const state2 &a)const{
return a.val < val;
}
};
priority_queue< state1 > q1;
priority_queue< state2 > q2;
const int INF = 1e9;
int head[N], n, m, u, v, l, r, d[N], h[N], tot, flag[N];
void add(int u, int v, int l, int r){
E[++tot].v = v;
E[tot].last = head[u];
E[tot].l = l;
E[tot].r = r;
head[u] = tot;
}
bool vis[N];
void dijkstra1(){
memset(vis, 0, sizeof vis);
while(!q1.empty()){
state1 u = q1.top(); q1.pop();
int x = u.x, val = u.val;
if(vis[x]) continue;
vis[x] = 1;
for(int i = head[x]; i; i = E[i].last){
int v = E[i].v, l = E[i].l, r = E[i].r;
if(h[x] > r){
if(h[v] < l + 1){
h[v] = l + 1;
q1.push((state1){v, h[v]});
}
}
}
}
}
void dijkstra2(){
memset(vis, 0, sizeof vis);
while(!q2.empty()){
state2 u = q2.top(); q2.pop();
int x = u.x, val = u.val;
if(vis[x]) continue;
vis[x] = 1;
for(int i = head[x]; i; i = E[i].last){
int v = E[i].v, l = E[i].l, r = E[i].r;
if(d[x] > r) continue;
if(h[v] <= r){
if(max(d[x], max(h[v], l)) < d[v]){
d[v] = max(d[x], max(h[v], l));
q2.push((state2){v, d[v]});
}
}
}
}
}
int main(){
freopen("lunch.in", "r", stdin);
freopen("lunch.out", "w", stdout);
n = read(), m = read();
for(int i = 1; i <= m; i++){
u = read(), v = read(), l = read(), r = read();
add(u, v, l, r);
add(v, u, l, r);
}
for(int i = 1; i <= n; i++){
flag[i] = read();
}
for(int i = 1; i <= n; i++){
if(flag[i] == -1) h[i] = INF, q1.push(state1{i, h[i]});
}
dijkstra1();
for(int i = 1; i <= n; i++){
if(h[1] > 0){
printf("Impossible\n");
return 0;
}
}
memset(d, 0x3f, sizeof d);
d[1] = 0;
q2.push((state2){1, 0});
dijkstra2();
for(int i = 1; i <= n; i++){
if(flag[i] == 1 && d[i] == 0x3f3f3f3f){
printf("Impossible\n");
return 0;
}
}
printf("JJXSM\n");
return 0;
}
C.老杰克哒

分析:
首先我们把区间内划分成若干
1
1
1 的连续段,那么对于一段,最多花费
2
2
2 的代价把它消除:我们可以现在后面加1,然后进位后在前面减1。并且一段至少需要花费1的代价。
基于上面的想法,我们可以考虑从后往前扫段,如果当前段长度大于1,那么就让它进位,否则就直接删掉。注意:进位后可能会与前面组成1段。所以这样做时肯定优的。贪心可以得到 50pts。
但是这样做没有什么优化的空间。我们考虑dp。
设
d
p
i
,
0
/
1
dp_{i, 0/1}
dpi,0/1 表示从开头到
i
i
i,字符串变成先一段连续的
0
0
0,然后一段连续的
0
/
1
0/1
0/1 的最小代价。考虑转移:
如果第 i i i 位是 0 0 0:
d
p
i
,
0
←
d
p
i
−
1
,
0
dp_{i, 0} \leftarrow dp_{i-1, 0}
dpi,0←dpi−1,0,
d
p
i
,
0
←
d
p
i
−
1
,
1
+
2
dp_{i,0} \leftarrow dp_{i-1, 1} + 2
dpi,0←dpi−1,1+2
d
p
i
,
1
←
d
p
i
−
1
,
0
+
1
dp_{i, 1} \leftarrow dp_{i - 1, 0} + 1
dpi,1←dpi−1,0+1,
d
p
i
,
1
←
d
p
i
−
1
,
1
+
1
dp_{i, 1} \leftarrow dp_{i - 1, 1} + 1
dpi,1←dpi−1,1+1
解释一下上面的转移, d p i , 0 dp_{i, 0} dpi,0 可以由 d p i − 1 , 0 dp_{i - 1, 0} dpi−1,0 转移而来,代表什么也不操作, d p i , 0 dp_{i, 0} dpi,0 由 d p i − 1 , 1 + 2 dp_{i - 1, 1} + 2 dpi−1,1+2 转移过来,代表我们可以通过加1减1两次操作把前面的一段1给消除完,这样多的花费是2。 d p i , 1 dp_{i, 1} dpi,1 的转移同理。
如果第 i i i 位是 1 1 1:
d
p
i
,
0
←
d
p
i
−
1
,
0
+
1
dp_{i, 0} \leftarrow dp_{i - 1, 0} + 1
dpi,0←dpi−1,0+1,
d
p
i
,
0
←
d
p
i
−
1
,
1
+
2
dp_{i, 0} \leftarrow dp_{i - 1, 1} + 2
dpi,0←dpi−1,1+2
d
p
i
,
1
←
d
p
i
−
1
,
0
dp_{i, 1} \leftarrow dp_{i - 1, 0}
dpi,1←dpi−1,0,
d
p
i
,
1
←
d
p
i
−
1
,
1
dp_{i, 1} \leftarrow dp_{i - 1, 1}
dpi,1←dpi−1,1。
这转移和上面的是同理的。
那么对每一次询问,我们设左端点是 s t st st,实际上就是按照 S s t S_{st} Sst 的类型给 d p s t , 0 / 1 dp_{st, 0/1} dpst,0/1 一个初值,然后 O ( n ) O(n) O(n)转移。
我们发现转移是取 m i n min min,并且这个转移方式只跟当前为字符是 0 0 0 还是 1 1 1 有关。并且和矩阵乘法很想。我们对应 0 0 0, 1 1 1,直接构造两种矩阵,然后用线段树维护区间内矩阵的乘积,加速转移就好了。
CODE:
#include<bits/stdc++.h>// 每一次转移可以看做是乘一个矩阵
using namespace std;// 用线段树维护矩阵的乘积
const int N = 3e5 + 10;
struct matrix{
int mt[2][2];
friend matrix operator * (matrix a, matrix b){
matrix c; memset(c.mt, 0x3f, sizeof c.mt);
for(int i = 0; i <= 1; i++)
for(int j = 0; j <= 1; j++)
for(int k = 0; k <= 1; k++)
c.mt[i][j] = min(c.mt[i][j], a.mt[i][k] + b.mt[k][j]);
return c;
}
};
matrix m1, m2;
struct SeqmentTree{
int l, r; matrix mt;
#define l(x) t[x].l
#define r(x) t[x].r
#define mt(x) t[x].mt
}t[N * 4];
int n, m, opt, x, y;
char str[N];
int read(){
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){if(c == '-') f = -1; c = getchar();}
while(isdigit(c)){x = (x << 1) + (x << 3) + (c ^ 48); c = getchar();}
return x * f;
}
void build(int p, int l, int r){
l(p) = l, r(p) = r;
if(l == r) return ;
int mid = (l + r >> 1);
build(p << 1, l, mid);
build(p << 1 | 1, mid + 1, r);
}
void update(int p){mt(p) = mt(p << 1) * mt(p << 1 | 1);}
void ins(int p, int pos, matrix c){
if(l(p) == r(p)){
mt(p) = c;
return ;
}
int mid = (l(p) + r(p) >> 1);
if(pos <= mid) ins(p << 1, pos, c);
else ins(p << 1 | 1, pos, c);
update(p);
}
matrix ask(int p, int l, int r){
if(l <= l(p) && r >= r(p)) return mt(p);
int mid = (l(p) + r(p) >> 1);
if(r <= mid) return ask(p << 1, l, r);
else if(l > mid) return ask(p << 1 | 1, l, r);
else return ask(p << 1, l, r) * ask(p << 1 | 1, l, r);
}
int query(int l, int r){
matrix res;
if(str[l] == '1') res.mt[0][0] = 1, res.mt[0][1] = 0;
else res.mt[0][0] = 0, res.mt[0][1] = 1;
if(l == r) return res.mt[0][0];
matrix tmp = ask(1, l + 1, r);
res = res * tmp;
return res.mt[0][0];
}
int main(){
freopen("string.in", "r", stdin);
freopen("string.out", "w", stdout);
n = read();
scanf("%s", str + 1);
int len = strlen(str + 1);
m1.mt[0][0] = 0; m1.mt[0][1] = 1; m1.mt[1][0] = 2; m1.mt[1][1] = 1;
m2.mt[0][0] = 1; m2.mt[0][1] = 0; m2.mt[1][0] = 2; m2.mt[1][1] = 0;
build(1, 1, n);
for(int i = 1; i <= len; i++){
if(str[i] == '0') ins(1, i, m1);
else ins(1, i, m2);
}
m = read();
for(int i = 1; i <= m; i++){
opt = read(), x = read(), y = read();
if(opt == 1) printf("%d\n", query(x, y));
else{
if(y == 0) ins(1, x, m1);
else ins(1, x, m2);
str[x] = (y + '0');
}
}
return 0;
}
D.季积晓淆
分析:
会不了一点 。