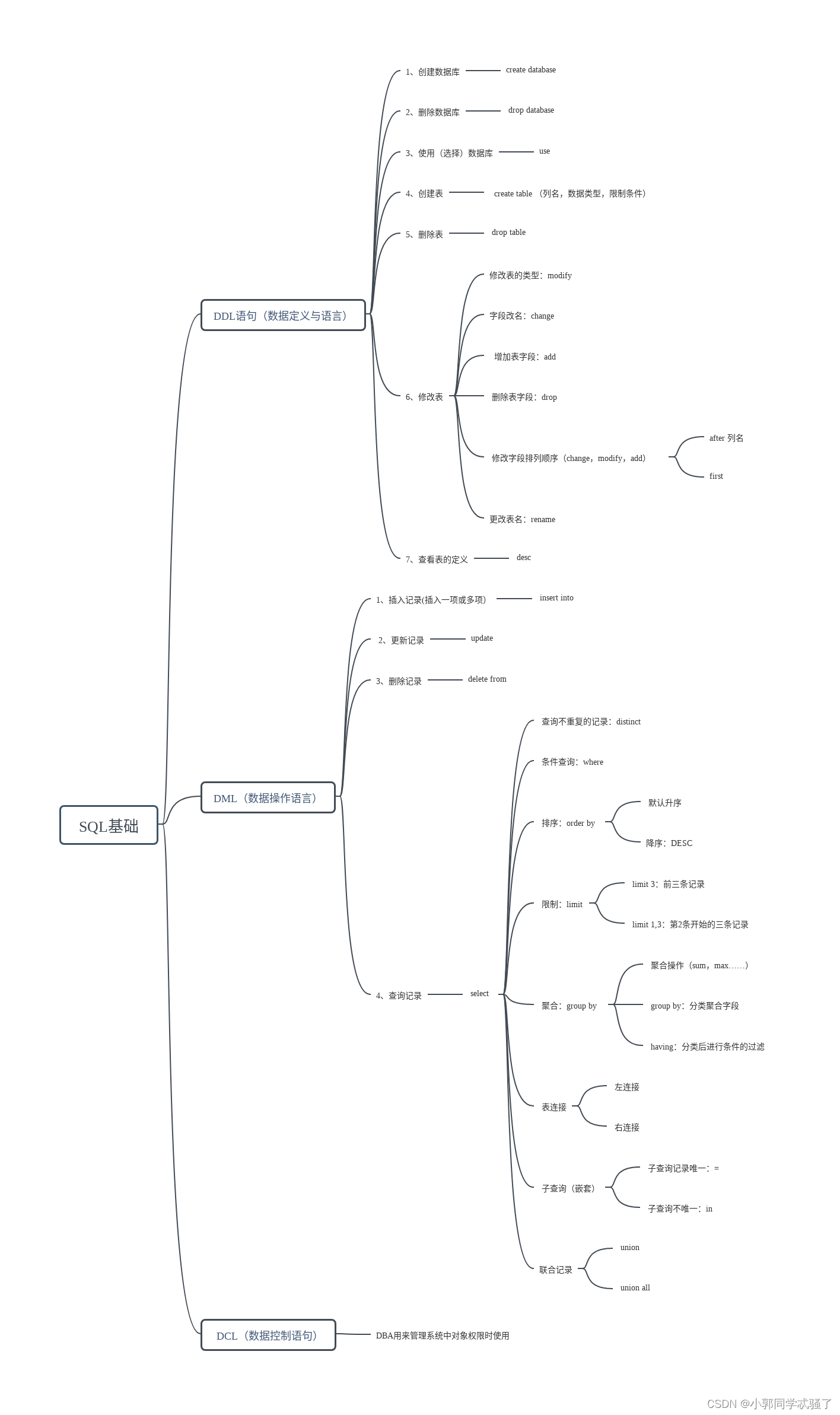
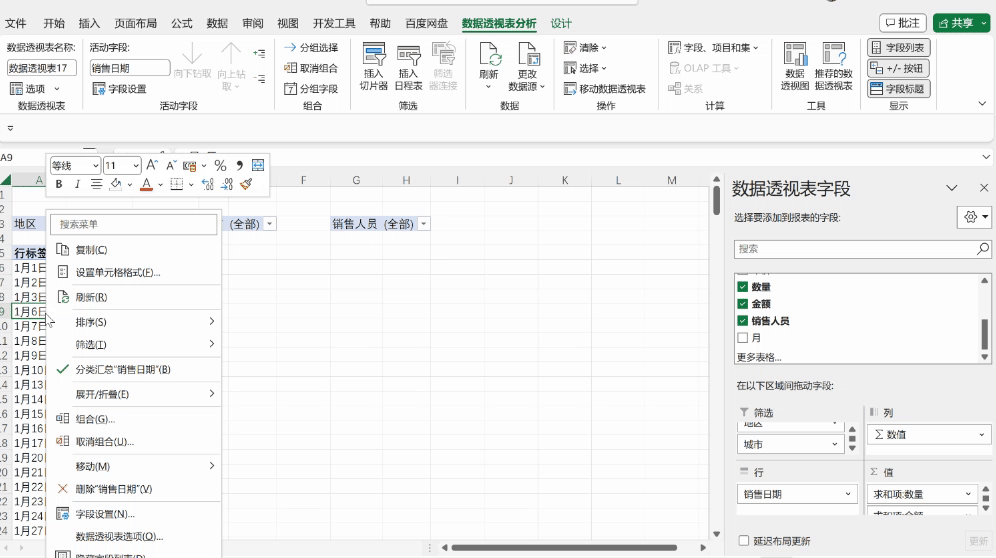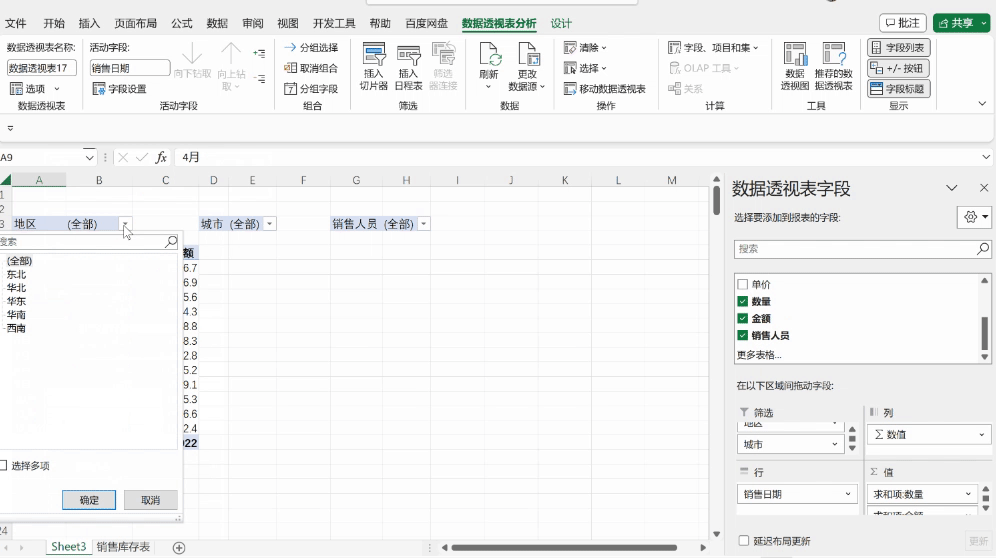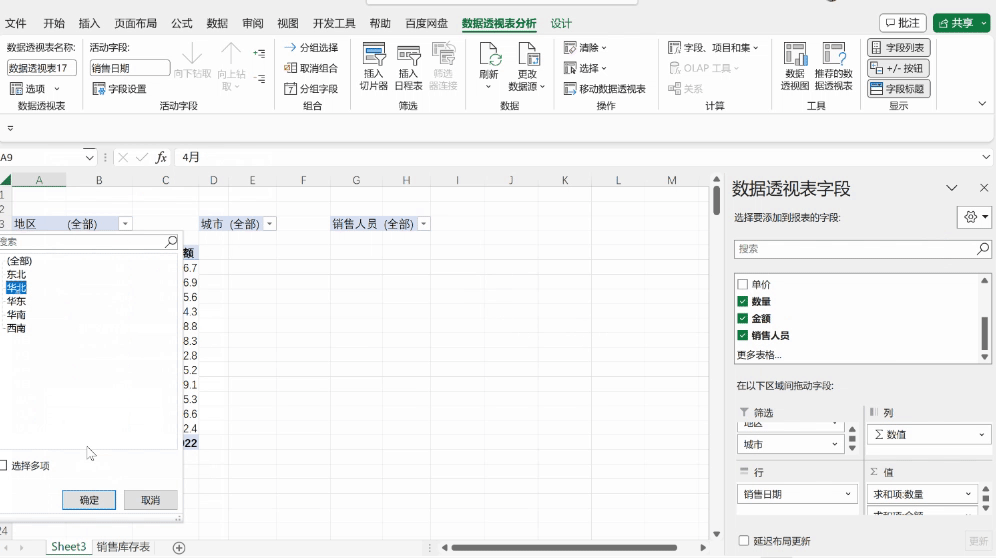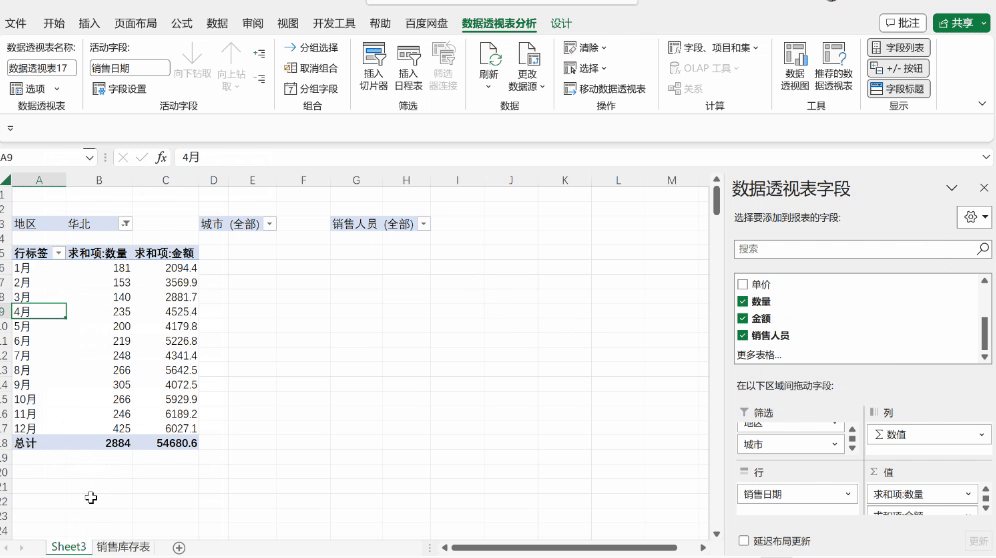
LeetCode 221. 最大正方形

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] 为 '0' 或 '1'

思路：

参考：LeetCode 视频题解并加以修改：LeetCode官方视频题解

注意：

• 在递推方程中 d[i][j] 代表的是 以坐标点 (i,j) 为【右下角】的正方形最大边长。
• 若某格子值为 1，则以此为右下角的正方形的最大边长为：上面的正方形、左面的正方形或左上的正方形中，最小的那个，再加上此格。即：min(上, 左, 左上) + 1

时间复杂度：O(mn)，其中 m 和 n 是矩阵的行数和列数

空间复杂度：O(mn)，其中 m 和 n 是矩阵的行数和列数

func maximalSquare(matrix [][]byte) int {
    m, n, maxLen := len(matrix), len(matrix[0]), 0
    
    // init dp array
    dp := make([][]int, m)
    for i := 0; i < m; i++ {
        dp[i] = make([]int, n)
    }

    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if matrix[i][j] == '1' {
                // 边界条件处理：自身格子为1的前提下，判断是否是第0行或第0列，避免越界
                if i == 0 || j == 0 {
                    dp[i][j] = 1
                } else {
                    // 以坐标点(i,j) 为【右下角】的正方形最大边长 = min(上, 左, 左上) + 1
                    dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1]) + 1 // +1：右下角的格子本身
                }

                if maxLen < dp[i][j] {
                    maxLen = dp[i][j]
                }
            }
        }
    }

    return maxLen*maxLen
}

func min(vals ... int) int {
    minVal := vals[0]
    for _, val := range vals {
        if val < minVal {
            minVal = val
        } 
    }
    return minVal
}

// func min(left, up, leftUp int) int {
//     arr := []int{left, up, leftUp}
//     sort.Ints(arr)
//     return arr[0]
// }

另外附上：自己在LeetCode上写的题解：我的题解