343. 整数拆分

题目要求：给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

示例 1:

• 输入: 2
• 输出: 1
• 解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

• 输入: 10
• 输出: 36
• 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
• 说明: 你可以假设 n 不小于 2 且不大于 58。

思路

dp[i]，分拆数字i，表示拆分到当前位置能够得到的乘积最大值。两种方法，一种是j*(i-j)，另一种是j*dp[i-j]。需要比较dp[i]和新乘积的关系。

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n+1);
        dp[2] = 1;
        for (int i = 3; i <= n; ++i) {
            for (int j = 1; j <= i/2; ++j) {
                dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j]));
            }
        }
        return dp[n];
    }
};

96. 不同的二叉搜索树

题目要求：给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

思路

dp[i]表示整数i最多能生成的二叉树个数，二叉搜索树的条件是左<中<右。n为1的时候有1棵二叉搜索树，n=2的时候有两棵，这都是直观的。

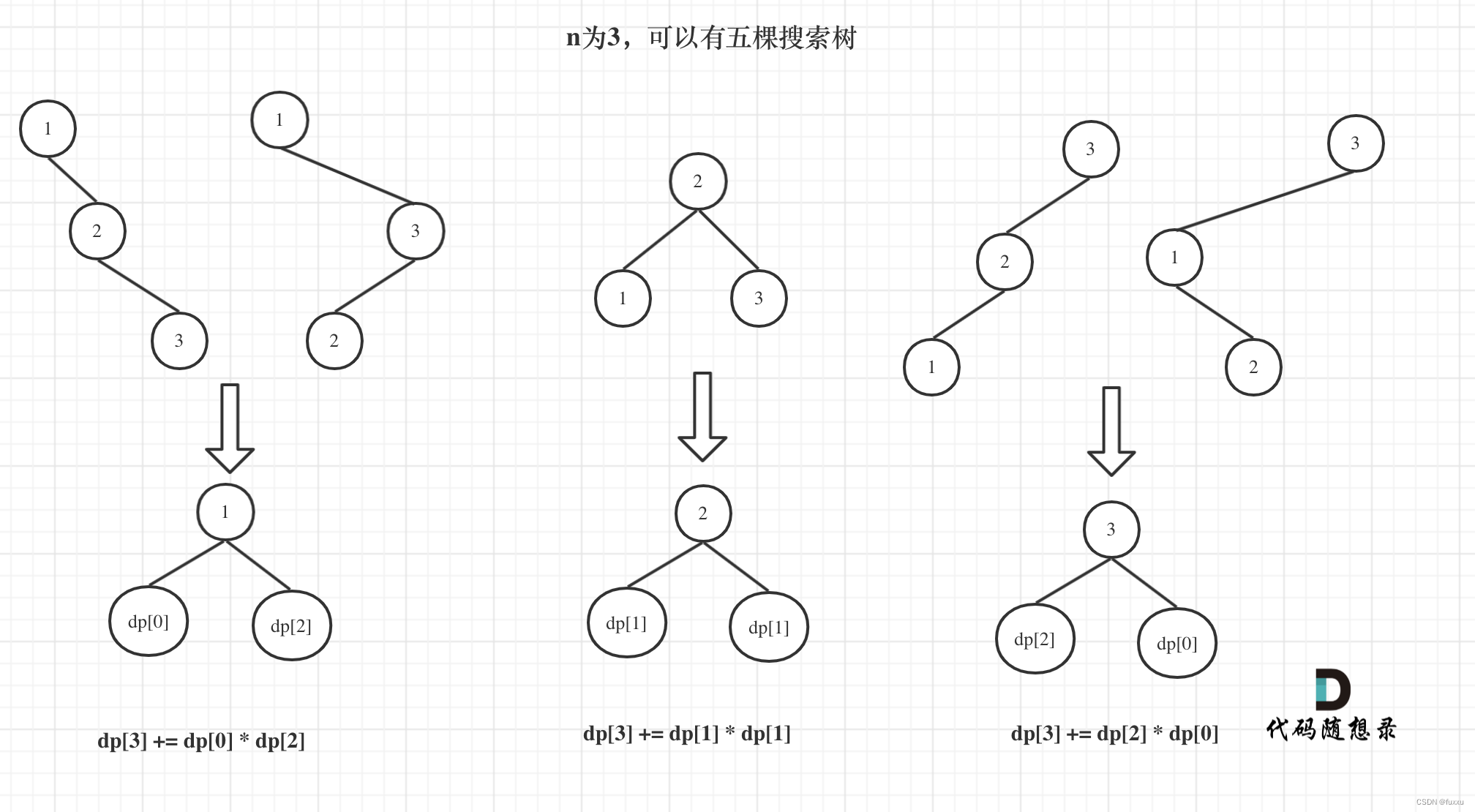
而n=3的时候能够生成5棵二叉搜索树。

以1为头节点的时候，右子树有两个节点，布局和n=2时候的两种布局是一致的。以2为头节点的时候，左右子树的布局和n=1的时候是一致的。可以通过dp[1]和dp[2]推导出dp[3]的某种模式。

dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量

元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量

元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量

元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]。

递推公式为，在上面的分析中，其实已经看出其递推关系， dp[i] += dp[以j为头结点左子树节点数量] * dp[以i-j为头结点右子树节点数量]

j相当于是头结点的元素，从1遍历到i为止。

所以递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量，dp[0]需要被初始化为1，尽管没有0个节点的二叉搜索树。

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n+1, 0);
        dp[0] = 1;
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= i; ++j) {
                dp[i] += dp[j-1] * dp[i-j];
            }
        }
        return dp[n];
    }
};

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$

总结

两个题目都是经典的递归题目，思路远大于代码复杂度的类型。需要通过举例推导递推关系式，通过小样本找规律得到递推关系。再通过调试和模拟找到初始化dp数组的值。