枚举：枚举所有的情况，逐个判断是否是问题的解

判断题目是否可以使用枚举：估算算法复杂度
1秒计算机大约能处理10⁷的数据量，即O(n)=10⁷，则O(n²)能处理的数据量就是根号10⁷≈3162

复杂度对应的数据量是该算法能处理的最大数据量
题目数据量n<在算法复杂度下能处理的最大数据量，则该算法可行

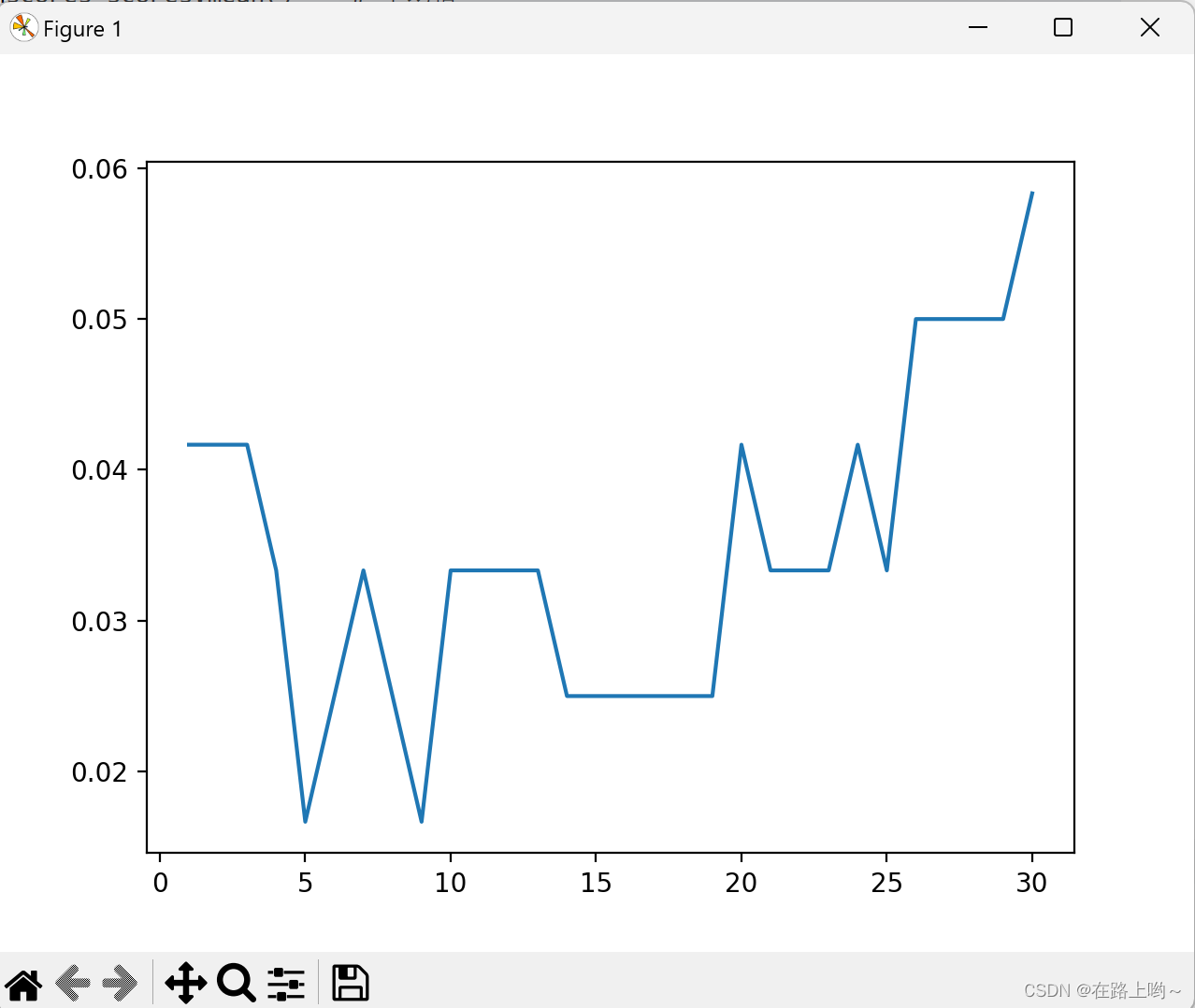
在1秒内各复杂度的算法能处理数据的量级↓

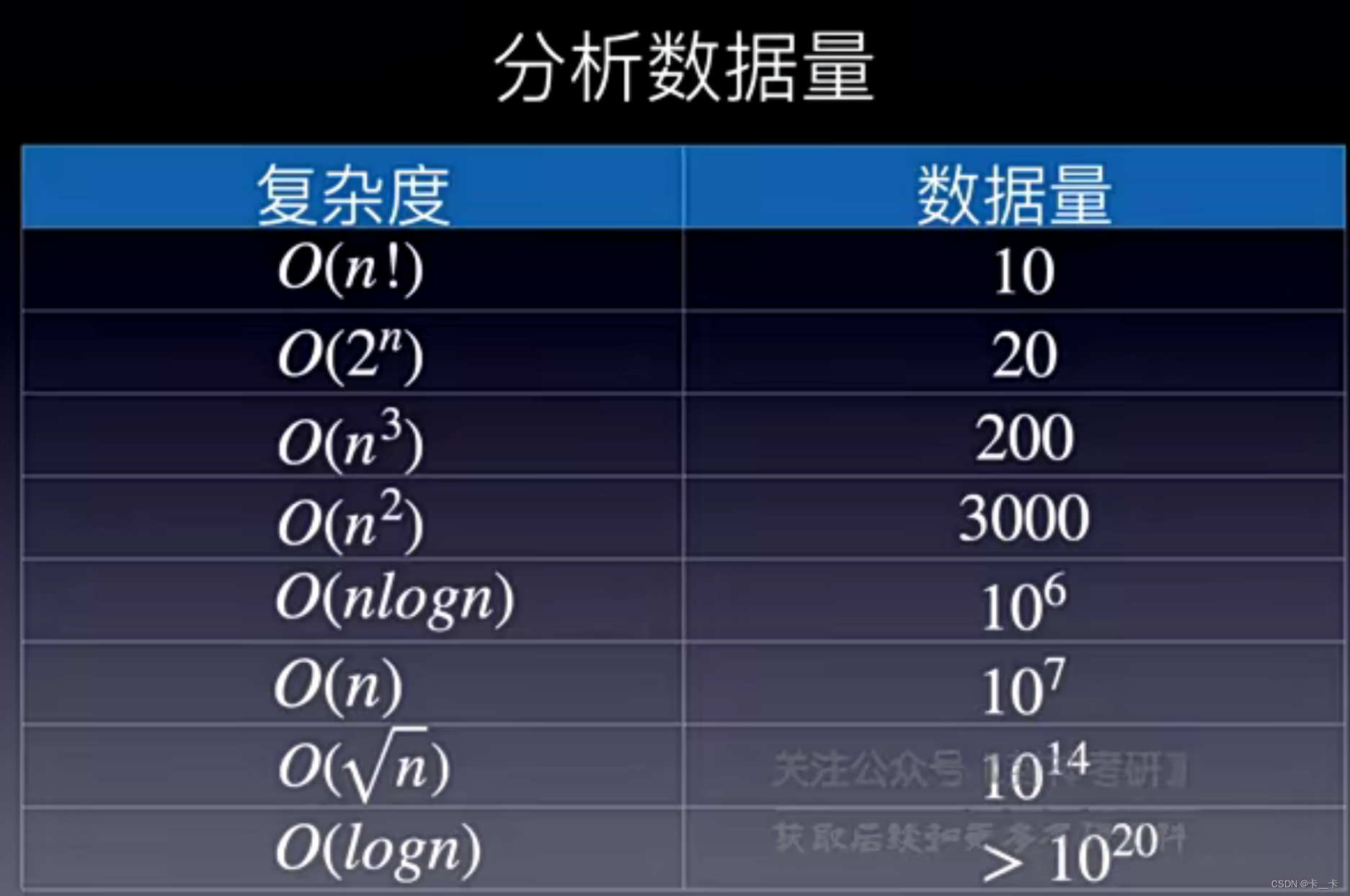
可以看出，若题目有10⁵的数据量，则不能采用O(n²)的算法，O(nlogn)是可以的

常见问题的复杂度

1.abc（清华大学）

评测系统

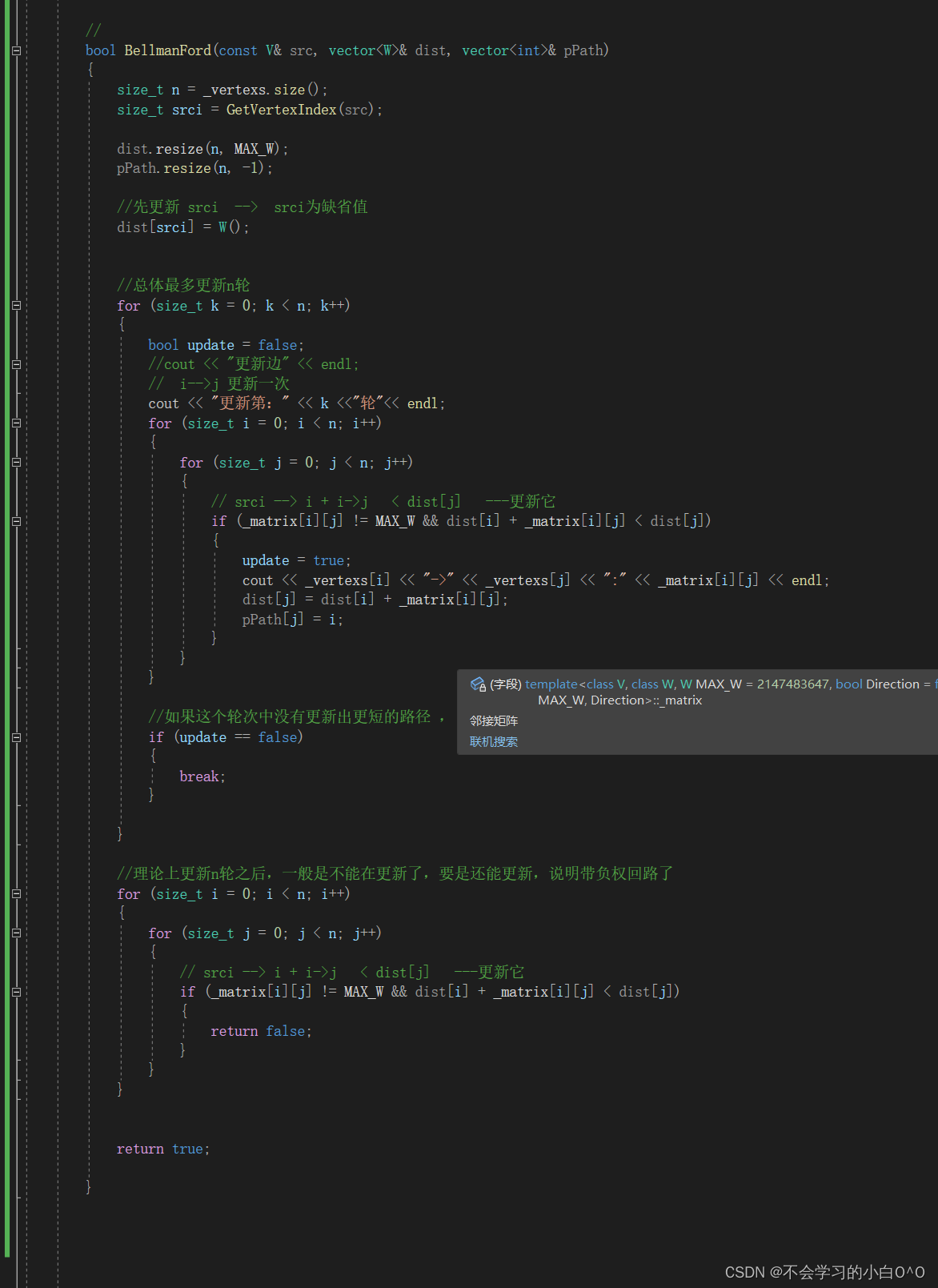
分析：题目的数据量n=10，可以采用三次for循环的方式，算法时间复杂度为O(n³)，能处理的数据量是200，10<200，算法可行

#include<iostream>
using namespace std;
int main() {
	for (int a = 0; a <= 9; a++) {
		for (int b = 0; b <= 9; b++) {
			for (int c = 0; c <= 9; c++) {
				if (100 * a + 10 * b + c + 100 * b + 10 * c + c == 532) {
					cout << a << " " << b << " " << c << endl;
				}
			}
		}
	}
}

2.反序数（清华大学）

评测系统

分析：四位数从1000到9999，数据量<10000，直接遍历复杂度O(n)。求反序数过程复杂度O(1)，总复杂度O(n)，能处理的数据量约为10⁷，10000<10⁷，算法可行

#include<iostream>
using namespace std;
int reverse(int x) {
	int sum = 0;
	while(x!=0){
		sum = sum*10 + x % 10;
		x = x / 10;
	}
	return sum;
}
int main() {
	for (int i = 1000; i <= 9999; i++) {
		if (i * 9 == reverse(i)) {
			cout << i << endl;
		}
	}
}

3.对称平方数（清华大学）

评测系统

注：数据>=0

分析：对称 → 原数=反序数

#include<iostream>
using namespace std;
int reverse(int x) {
	int sum=0;
	while (x) {
		sum = sum * 10 + x % 10;
		x = x / 10;
	}
	return sum;
}
int main() {
	for (int i = 0; i <= 256; i++) {
		if (i*i==reverse(i*i)) {
			cout << i << endl;
		}
	}
}

4.与7无关的数（北京大学）

评测系统

#include<iostream>
using namespace std;
bool relate2(int x) { //判断某位数字是否为7
	while (x) {
		if (x % 10 == 7)
			return true;
		x = x / 10;
	}
	return false;
}
bool relate(int x) { //判断是否与7相关
	if (x % 7 == 0)
		return true;
	else if (relate2(x)) {
		return true;
	}
	else
		return false;
}
int main() {
	int sum = 0;
	int n=0;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		if (!relate(i)) {
			sum += i * i;
		}
	}
	cout << sum;
}

5.百鸡问题（哈尔滨工业大学）

评测系统

分析：xyz的取值最大为100，采用三次for循环的方式，算法时间复杂度为O(n³)，能处理的数据量是200，100<200，算法可行；1/3的等式两边同乘3化为整数

#include<iostream>
using namespace std;
int main() {
	int n = 0;
	cin >> n;
	for (int x = 0; x <= 100; x++) {
		for (int y = 0; y <= 100; y++) {
			for (int z = 0; z <= 100; z++) {
				if (15 * x + 9 * y + z <= 3*n && x + y + z == 100)
					printf("x=%d,y=%d,z=%d\n", x, y, z);
			}
		}
	}
}

6.Old Bill（上海交通大学）

评测系统

#include<iostream>
using namespace std;
int main() {
	int N = 0;
	int first, x, y, z, last, pricemax = 0;
	while (cin >> N) {
		cin >> x >> y >> z;
		if (N == 0) {
			cout << 0;
			break;
		}
		bool flag = 0;
		for (int i = 1; i <= 9; i++) {
			for (int j = 0; j <= 9; j++) {
				int temp = 10000 * i + 1000 * x + 100 * y + 10 * z + j;
				if (temp < N) {
					break;
				}
				if (temp % N == 0 && temp / N > pricemax) {
					pricemax = temp / N;
					first = i;
					last = j;
					flag = 1;
				}
			}
		}
		if (flag == 1)
			cout << first << " " << last << " " << pricemax << endl;
		else {
			cout << 0 << endl;
		}
		flag = 0;
	}
}