详解numpy.meshgrid()方法使用

news2024/11/19 1:48:06

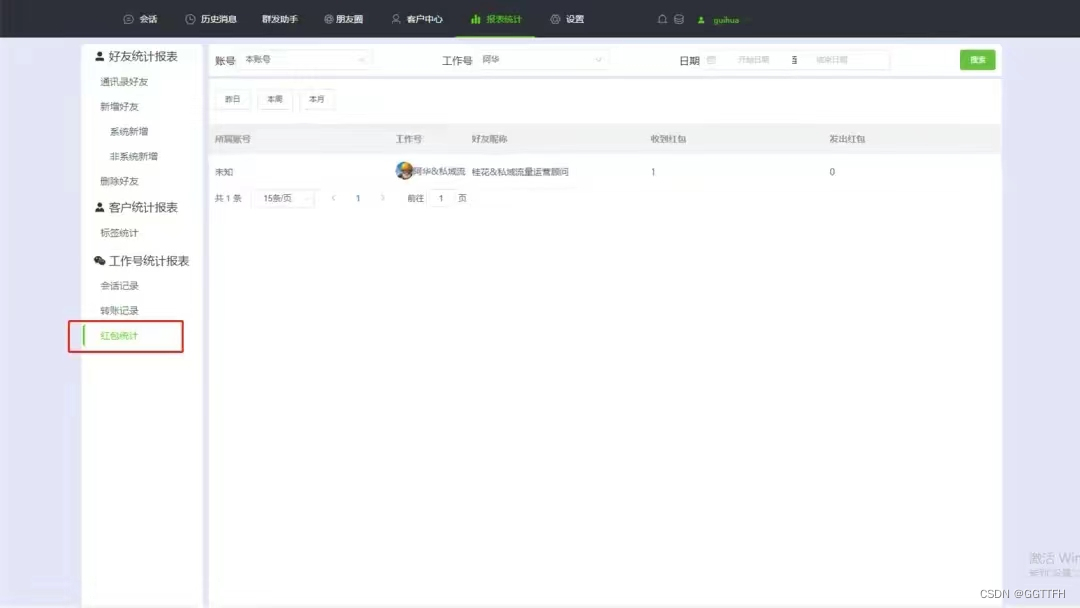
这篇文章主要介绍了详解numpy.meshgrid()方法使用，文中通过示例代码介绍的非常详细，对大家的学习或者工作具有一定的参考学习价值。

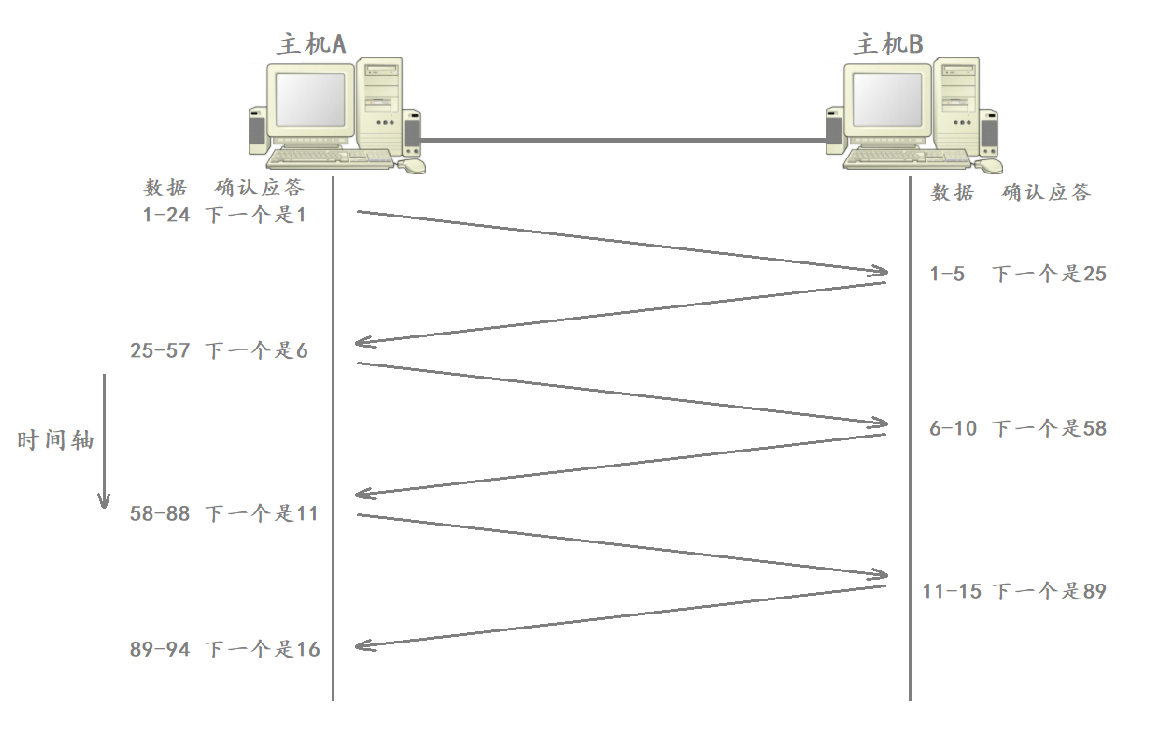
一句话解释numpy.meshgrid()——生成网格点坐标矩阵。

网格点是什么？坐标矩阵又是什么鬼？看个图就明白了：

图中，每个交叉点都是网格点，描述这些网格点的坐标的矩阵，就是坐标矩阵。

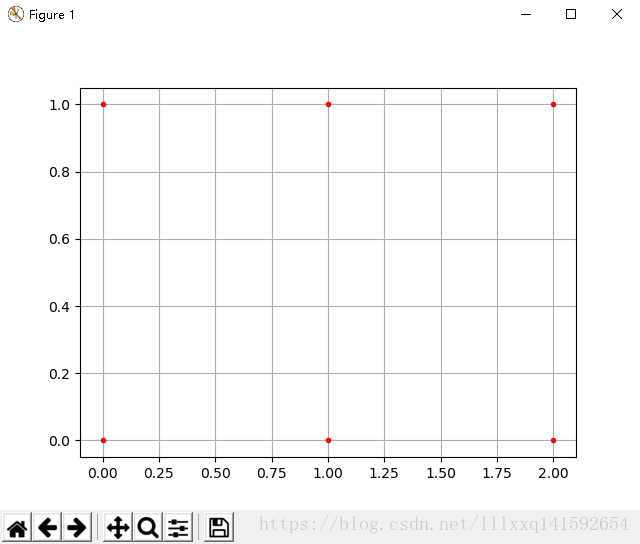
再看个简单例子

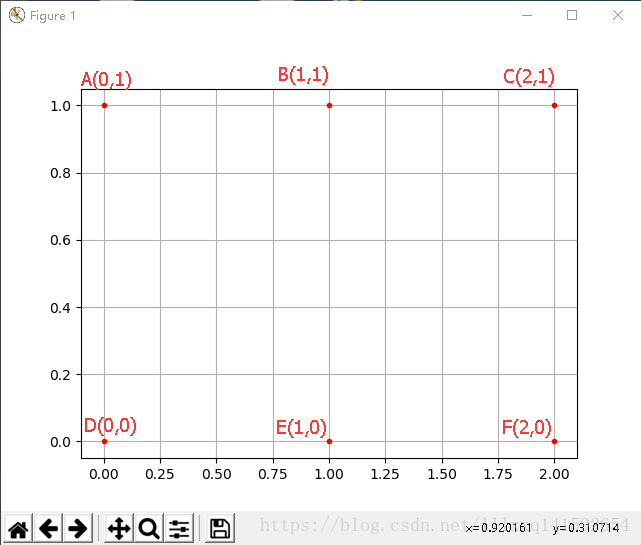
A,B,C,D,E,F是6个网格点，坐标如图，如何用矩阵形式（坐标矩阵）来批量描述这些点的坐标呢？

答案如下：

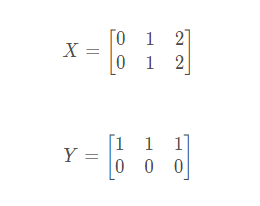
这就是坐标矩阵——横坐标矩阵XXX中的每个元素，与纵坐标矩阵YYY中对应位置元素，共同构成一个点的完整坐标。如B点坐标

下面可以自己用matplotlib来试一试，输出就是上边的图

1

2

3

4

5

6

7

8

9

10

11

12

13

import numpy as np

import matplotlib.pyplot as plt

x = np.array([[0, 1, 2], [0, 1, 2]])

y = np.array([[0, 0, 0], [1, 1, 1]])

plt.plot(x, y,

   color='red', # 全部点设置为红色

   marker='.', # 点的形状为圆点

   linestyle='') # 线型为空，也即点与点之间不用线连接

plt.grid(True)

plt.show()

如果对matplotlib不熟悉，可能只知道用一列横坐标（线性代数中的1维列向量），一列纵坐标生成（两者元素个数相等）一些点。但是实际上，给matplotlib的坐标信息是矩阵也是可以的，只要横纵坐标的尺寸一样。都会按照对应关系生成点。

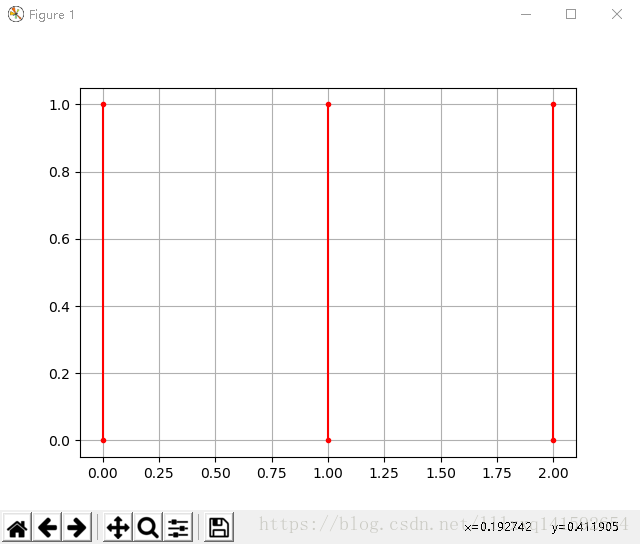
但是有需要注意的地方，按照矩阵给坐标点信息，matplotlib会把横坐标矩阵中，每一列对应的点当做同一条线。

举个例子，把上面的代码plot的linestyle=''删掉，或者变成linestyle='-'（这个操作把图的线型改为默认状态），就会发现A-D是连接的，B-E是连接的，C-F是连接的，也即，会认为你输入的是3条线，如图

作为练习，自己试着生成如下结果

提示：线型等关键字参数设置可用如下代码

1

2

3

4

plt.plot(x, y,

   marker='.', # 点的形状为圆点

   markersize=10, # 点设置大一点，看着清楚

   linestyle='-.') # 线型为点划线

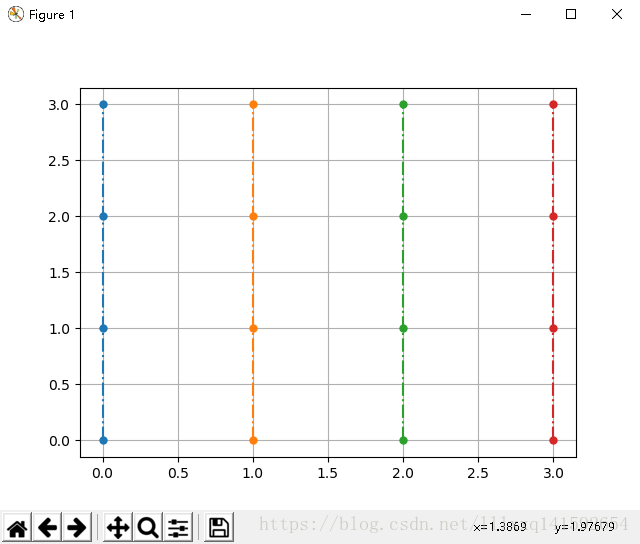
答案

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

import numpy as np

import matplotlib.pyplot as plt

x = np.array([[0, 1, 2, 3],

    [0, 1, 2, 3],

    [0, 1, 2, 3],

    [0, 1, 2, 3]])

y = np.array([[0, 0, 0, 0],

    [1, 1, 1, 1],

    [2, 2, 2, 2],

    [3, 3, 3, 3]])

plt.plot(x, y,

   marker='.', # 点的形状为圆点

   markersize=10, # 点设置大一点，看着清楚

   linestyle='-.') # 线型为点划线

plt.grid(True)

plt.show()

到这里，网格点和坐标矩阵的概念就解释清楚了。

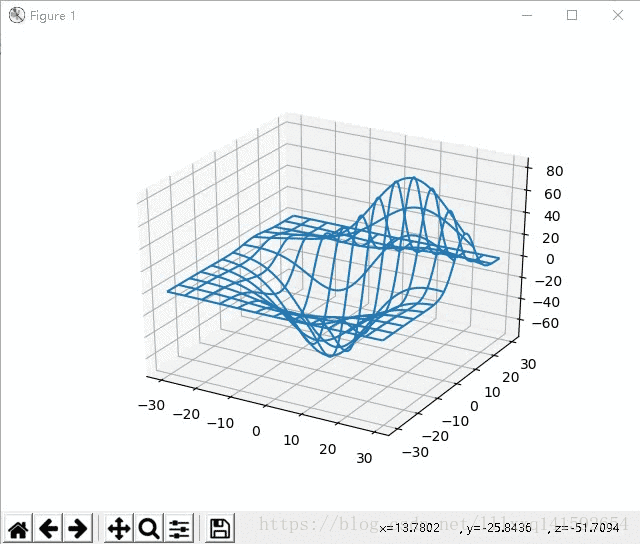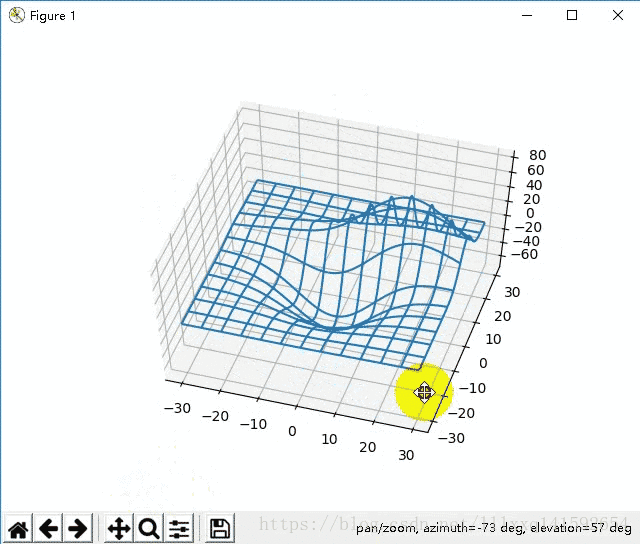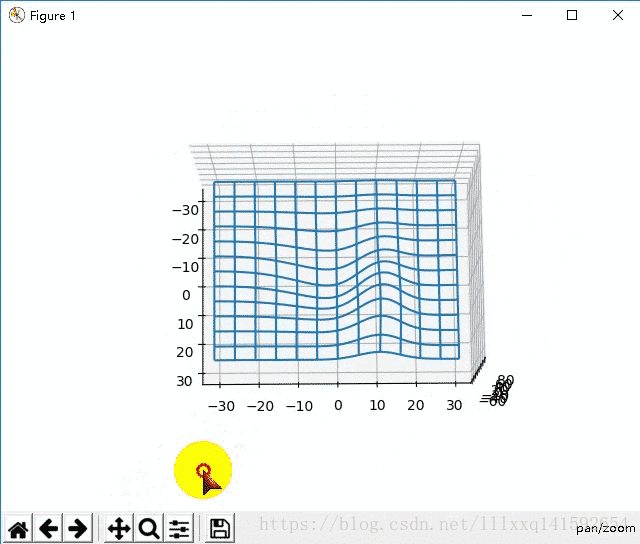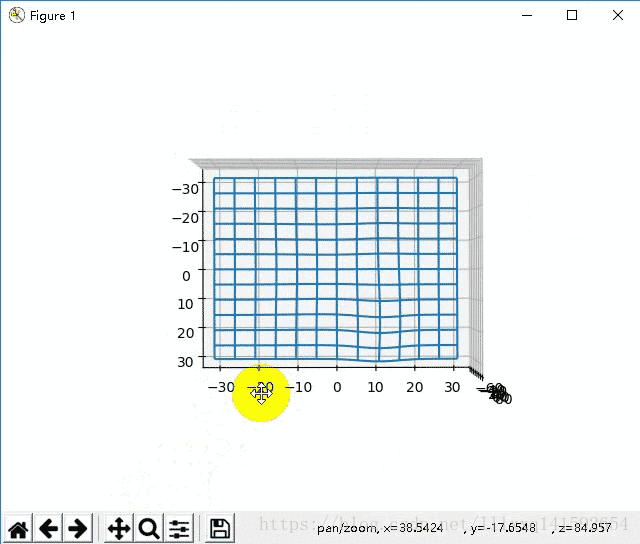
那么问题来了，如果需要的图比较大，需要大量的网格点该怎么办呢？比如下面的这种

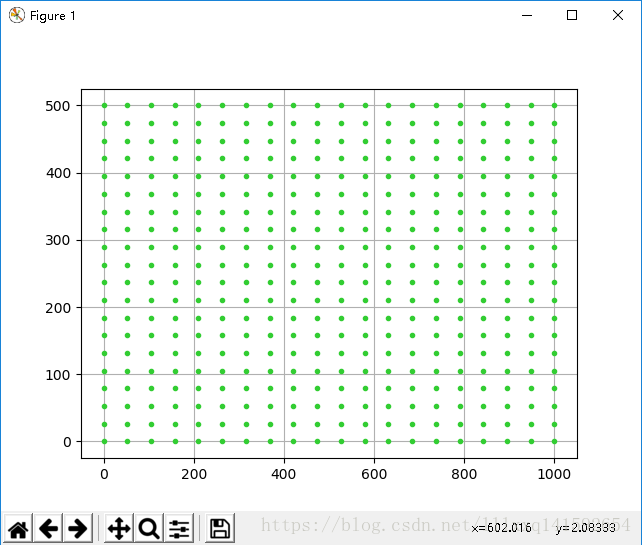
最直接但是最笨的方法，就是按照上面的方法把横纵坐标矩阵XXX，YYY写出来，就像上面练习题中的

很明显，对于网格点很多的情况根本没法用。有啥好的办法吗？

有的，注意到我们练习题中的坐标矩阵，其实有大量的重复——XXX的每一行都一样，YYY的每一列都一样。基于这种强烈的规律性，numpy提供的numpy.meshgrid()函数可以让我们快速生成坐标矩阵XXX，YYY。

语法：X,Y = numpy.meshgrid(x, y)

输入的x，y，就是网格点的横纵坐标列向量（非矩阵）
输出的X，Y，就是坐标矩阵。

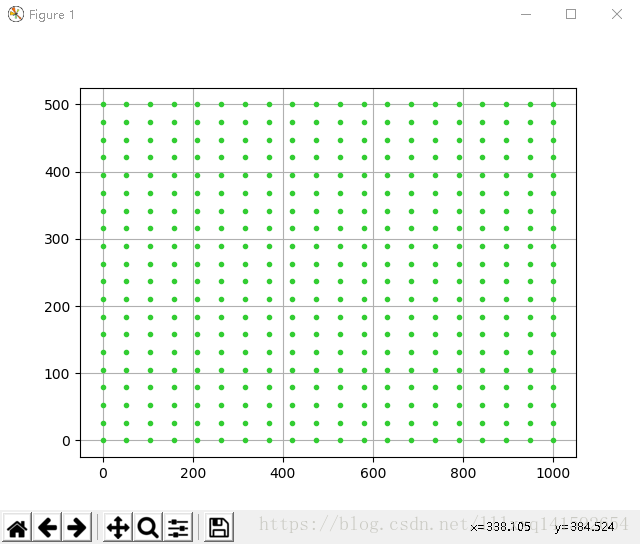
我们来试验一下：改写第一个例子中的代码，用numpy.meshgrid来实现。

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

import numpy as np

import matplotlib.pyplot as plt

x = np.array([0, 1, 2])

y = np.array([0, 1])

X, Y = np.meshgrid(x, y)

print(X)

print(Y)

plt.plot(X, Y,

   color='red', # 全部点设置为红色

   marker='.', # 点的形状为圆点

   linestyle='') # 线型为空，也即点与点之间不用线连接

plt.grid(True)

plt.show()

1

2

3

4

5

# 从输出的结果来看，两种方法生成的坐标矩阵一毛一样。

[[0 1 2]

 [0 1 2]]

[[0 0 0]

 [1 1 1]]

最后给出上面这个图的代码

1

2

3

4

5

6

7

8

9

10

11

12

13

14

import numpy as np

import matplotlib.pyplot as plt

x = np.linspace(0,1000,20)

y = np.linspace(0,500,20)

X,Y = np.meshgrid(x, y)

plt.plot(X, Y,

   color='limegreen', # 设置颜色为limegreen

   marker='.', # 设置点类型为圆点

   linestyle='') # 设置线型为空，也即没有线连接点

plt.grid(True)

plt.show()

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1155390.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

公司员工的销售微信号如何管理？

公司员工的销售微信号如何管理？

在当今数字化时代，微信已成为企业营销的重要工具之一。其中，公司员工的销售微信号更是企业拓展业务、提高品牌知名度的重要途径。然而，如何有效管理这些销售微信号，确保其正常运行并避免潜在风险，已成为许多企业面临的…
阅读更多...
IOI车机系统刷机和改包笔记2 - 改包脚本

IOI车机系统刷机和改包笔记2 - 改包脚本

前言： 最近对雪佛兰改包需求感兴趣的网友很多，大家都遇上了很多奇怪的问题，这里就我自己使用的环境和脚本进行分享，供大家参考。 1. 准备环境 我这里使用Ubuntu系统进行操作 andyandy-vm:~$ sudo lsb_release -a No LSB module…
阅读更多...
Web3 React项目Dapp获取智能合约对象

Web3 React项目Dapp获取智能合约对象

上文Web3 整理React项目 导入Web3 并获取区块链信息中，我们在react搭建的dapp中简单拿到了我们区块链中的账号授权信息 那 我们继续 先终端运行 ganache -d将ganache环境起起来 然后 我们运行 dapp 拿到授权列表 回到上文结束的一个状态 然后 我们发布一下自己的…
阅读更多...
Qt 常用方法 获取磁盘总大小、可用空间、文件夹大小 文件大小B KB M G转换

Qt 常用方法 获取磁盘总大小、可用空间、文件夹大小 文件大小B KB M G转换

1.通过QFile获取文件大小 注意&#xff1a;返回的是字节个数 QFile file("E:/59.raw");if (file.open(QIODevice::ReadOnly)) {qDebug() << file.size();// byte} else {qDebug() << "文件打开失败&#xff01;";} 通过QFileInfo获取文件大小…
阅读更多...
初识CSS层叠样式表

初识CSS层叠样式表

文章目录 CSS介绍CSS层叠样式表1.CSS组成2.CSS语法结构3.注释语法4.引入CSS的多种方式 CSS选择器1.CSS基础选择器2.CSS组成选择器3.分组与嵌套4.CSS属性选择器5.CSS伪类选择器6.CSS伪元素选择器 选择器优先级CSS继承选择器的优先级 CSS样式调节字体样式文本颜色文本属性 边框di…
阅读更多...
c++从入门到放弃,小白踩坑记录1

c++从入门到放弃,小白踩坑记录1

c从入门到放弃,小白踩坑记录1 错误问题描述 没有与这些操作数匹配的运算符操作数类型为std::basic_ostream <char,std::char traits <char > > < < <unknown-type > 错误代码 #include<iostream> int main(void) {std::cout << "…
阅读更多...
从小白到精通：揭秘perf工具的全部功能与操作技巧

从小白到精通：揭秘perf工具的全部功能与操作技巧

揭秘perf工具的全部功能与操作技巧 一、引言二、理解perf工具的基本概念三、安装与配置perf工具3.1、不同操作系统的perf工具安装3.2、perf工具的配置选项和环境设置 四、perf工具的常用命令和功能4.1、perf工具的基本命令结构和常用参数4.2、perf工具的常见用法和功能4.3、per…
阅读更多...
医学AI智能导诊系统源码

医学AI智能导诊系统源码

医院智能导诊系统是一款基于人工智能和大数据技术开发的医疗辅助软件&#xff0c;旨在为患者提供更加便捷、精准的医疗服务。 一、什么是智能导诊系统&#xff1f; 智能导诊系统是一种基于人工智能和大数据技术开发的医疗辅助软件&#xff0c;它能够通过对患者的症状、病史等信…
阅读更多...
Qt扫盲-QFontDatabase理论

Qt扫盲-QFontDatabase理论

QFontDatabase理论 一、概述二、常用功能 一、概述 QFontDatabase 类提供有关底层窗口系统中可用字体的信息。 这个类最常见的用途是查询数据库中的字体系列列表()以及每个系列可用的 pointSizes() 和 styles()。pointSizes() 的另一种替代方法 是smoothSizes()&#xff0c;它…
阅读更多...
使用传感器融合的前方碰撞预警-(Forward Collision Warning Using Sensor Fusion)

使用传感器融合的前方碰撞预警-(Forward Collision Warning Using Sensor Fusion)

这个例子matlab自动驾驶工具箱中关于使用传感器融合的前方碰撞预警-(Forward Collision Warning Using Sensor Fusion)例子&#xff0c;其展示了如何通过融合视觉和雷达传感器的数据来跟踪车辆前方的物体&#xff0c;从而实现前向碰撞预警系统的开发与验证。 1 概述 前方碰撞…
阅读更多...
Java体系性能测试进阶必须了解的知识点——Thread Dump

Java体系性能测试进阶必须了解的知识点——Thread Dump

Thread Dump定义 Java Thread dump记录了线程在jvm中的执行信息&#xff0c;可以看成是线程活动的日志。Java线程转储文件有助于分析应用程序和死锁情况中的瓶颈。Thread Dump是非常有用的诊断Java应用问题的工具。它提供了当前活动线程的快照及JVM中所有Java线程的堆栈跟踪信…
阅读更多...
【计算机网络】传输层——TCP

【计算机网络】传输层——TCP

目录 1.概念2.可靠性概念3.TCP协议格式序号和确认序号窗口大小六个标志位 4.TCP可靠性保障确认应答机制&#xff08;ACK&#xff09;超时重传机制连接管理机制流量控制拥塞控制 5.TCP提高性能滑动窗口延迟应答捎带应答 6.面向字节流7.粘包问题8.TCP异常情况9.TCP总结 1.概念 T…
阅读更多...
MES 价值点之数据追随

MES 价值点之数据追随

在现代制造业中&#xff0c;数据追溯已经越来越得到重视&#xff0c;特别是那些推行精益生产的企业重要性就更加突出了&#xff0c;而制造执行系统&#xff08;MES&#xff09;作为一种关键的生产管理工具&#xff0c;是能很好的为制造企业提供数据追溯功能。今天&#xff0c;和…
阅读更多...
基因家族扩张与收缩分析-CAFE5

基因家族扩张与收缩分析-CAFE5

CAFE(Computational Analysis of gene Family Evolution)是一款以解释系统发育历史的方式分析基因家族大小变化的软件&#xff0c;这种分析常被称为基因家族收缩扩张(Gene family expansions and contractions)分析。 CAFE使用出生和死亡过程来模拟用户指定的系统发育树中的基…
阅读更多...
剑指JUC原理-7.线程状态与ReentrantLock

剑指JUC原理-7.线程状态与ReentrantLock

&#x1f44f;作者简介&#xff1a;大家好&#xff0c;我是爱吃芝士的土豆倪&#xff0c;24届校招生Java选手&#xff0c;很高兴认识大家&#x1f4d5;系列专栏&#xff1a;Spring源码、JUC源码&#x1f525;如果感觉博主的文章还不错的话&#xff0c;请&#x1f44d;三连支持&…
阅读更多...
Linux的开发环境安装配置与后端项目部署

Linux的开发环境安装配置与后端项目部署

目录 一.安装开发环境 1.准备阶段 1.1 创建新目录 1.2 解压文件 2.JDK的安装与配置环境变量 2.1 解压jdk压缩包 2.2 配置环境变量 2.3 设置环境变量生效 2.4 验证是否安装成功 3.Tomcat的安装与使用 3.1 解压安装 3.2 开启服务 3.3 开放端口 3.4 访问成功 4.MySQ…
阅读更多...
Python的错误和异常处理

Python的错误和异常处理

一、错误和异常 编程中出现的错误大致可以分为两类&#xff1a;错误和异常。 (一)错误 错误又可以分为两类&#xff1a;语法错误和逻辑错误。 1. 语法错误 语法错误又称解析错误&#xff0c;它是指在编写程序时&#xff0c;程序的语法不符合Python语言的规范&#xff0c;导致…
阅读更多...
虚拟机和Windows的文件传输

虚拟机和Windows的文件传输

拖拽/复制粘贴 直接将虚拟机linux系统的文件拖曳到windows桌面&#xff0c;或者直接将windows的文件拖曳到虚拟机linux系统当中&#xff0c;可以实现文件传输。当然复制粘贴方式也可以&#xff0c;但是前提是需要下载安装好VMware tools。 共享文件夹 概念&#xff1a;在Win…
阅读更多...
阿里在盘古云存储系统中部署RDMA的经验谈

阿里在盘古云存储系统中部署RDMA的经验谈

1 阿里如何进行RDMA部署 1.1 RDMA部署规划中的考虑因素 存储集群的部署规划控制着网络拓扑结构、RDMA通信范围、存储节点配置等&#xff0c;必须考虑多种因素&#xff0c;包括存储容量与需求的匹配、硬件成本的控制、性能的优化、可用性和SLA风险的最小化。最终的结果是所有这…
阅读更多...
cmake构建多项目编译

cmake构建多项目编译

项目结构如下 CMakeLists清单 最外层的主CMakeLists cmake_minimum_required(VERSION 3.17) project(cmakeMulPackage)set(CMAKE_CXX_STANDARD 11)#添加一个子目录并构建该子目录 add_subdirectory(proj1) add_subdirectory(proj2)#定义头文件路径 include_directories(proj1…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023