高效处理大规模数据集的概率型数据结构—— 布隆过滤器 [C++入门]

news2024/11/20 16:31:11

在这里插入图片描述

阅读导航

  • 引言
  • 一、布隆过滤器提出
  • 二、布隆过滤器的概念
  • 三、布隆过滤器的实现
    • 1. 插入
    • 2. 查找
    • 3. 删除（不支持）
    • C++模拟实现布隆过滤器
  • 四、布隆过滤器的优缺点
    • ✅优点
    • ✅缺点

引言

🍔在上一篇文章位图中，我们了解了C++中位图的概念和实现。位图是一种用于表示和操作大量二进制位的数据结构，它在解决需要高效存储和操作布尔类型数据的问题上具有重要作用。而在本篇文章中，我们将继续探讨另一个在C++中常用的数据结构——布隆过滤器。布隆过滤器是一种概率型数据结构，它可以高效地判断一个元素是否存在于一个集合中，同时具备较小的内存占用和快速查询的特点。通过对比位图和布隆过滤器的实现原理和应用场景，我们可以更全面地了解不同数据结构在C++中的应用。接下来，让我们深入探索布隆过滤器的奥秘吧！坐稳扶好咱们要开车了😍

一、布隆过滤器提出

🍪在我们日常生活中我们一定会收到不少的垃圾邮件所以我们有时候会开启自动过滤垃圾邮件，垃圾邮件过滤中，布隆过滤器可以快速判断一个邮件发送者是否为垃圾邮件发送者，从而减少用户收到垃圾邮件的数量。要想实现上面的功能我们需要从数据库中寻找出来并判断是不是垃圾邮件经常发送者。那么如何快速查找呢？

  1. 用哈希表存储用户记录，缺点：浪费空间
  2. 用位图存储发送者的信息，缺点：位图一般只能处理整形，如果发送者信息是字符串，就无法处理了。
  3. 将哈希与位图结合，即布隆过滤器

二、布隆过滤器的概念

🍁布隆过滤器是由布隆（Burton Howard Bloom）在1970年提出的一种概率型数据结构，用于快速判断一个元素是否存在于一个集合中。它通过使用多个哈希函数和位数组来实现，具有较小的内存占用和快速查询的特点。由于其高效的元素存在性判断能力，布隆过滤器在各种应用场景中得到了广泛的应用。

🍁然而，布隆过滤器也存在一定的缺点。首先，它是一个概率型数据结构，存在一定的误判率。即使一个元素不存在于集合中，也有可能被误判为存在。其次，布隆过滤器不支持删除操作，因为删除一个元素会影响到其他元素的判断结果。最后，由于使用了多个哈希函数和位数组，布隆过滤器的构建和查询操作需要一定的计算资源。

🍁在实际应用中，我们可以根据具体的需求和数据特点来选择合适的布隆过滤器参数，如位数组长度、哈希函数数量等，以达到较低的误判率和较高的性能。同时，我们需要注意布隆过滤器的误判率与插入元素数量、位数组长度和哈希函数数量等因素相关，需要合理权衡这些参数，以满足实际应用的需求。

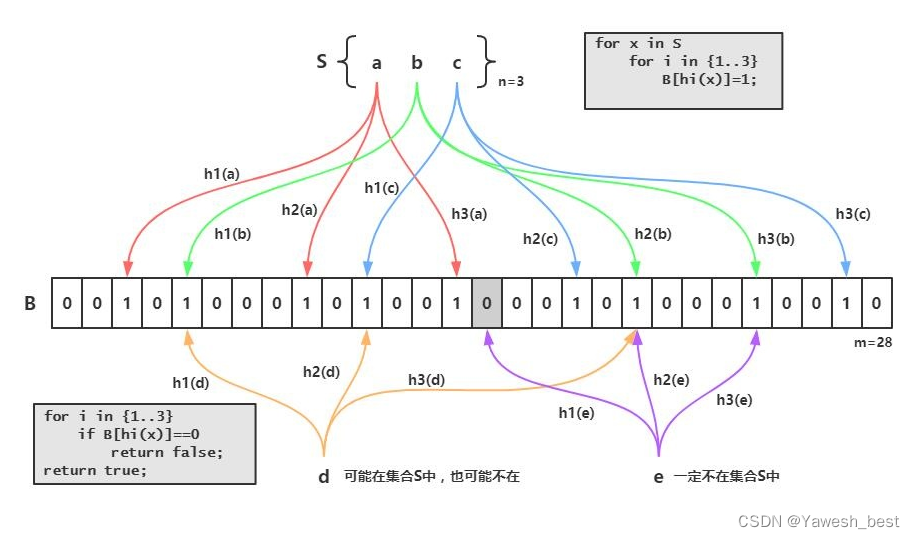
在这里插入图片描述

三、布隆过滤器的实现

1. 插入

布隆过滤器是一种快速判断某个元素是否存在于一个集合中的数据结构，它通过哈希函数将元素映射到位数组中的多个位置，并将这些位置标记为1。

void set(const K& key)
{
	size_t len = N * _X;
	size_t hash1 = Hash1()(key) % len;
	_bs.set(hash1);

	size_t hash2 = Hash2()(key) % len;
	_bs.set(hash2);

	size_t hash3 = Hash3()(key) % len;
	_bs.set(hash3);

}

具体来说，set函数接受一个键值key作为参数，将其哈希后的值映射到位数组中的多个位置，并将这些位置标记为1。这里使用了三个不同的哈希函数 H a s h 1 Hash1 Hash1、 H a s h 2 Hash2 Hash2和 H a s h 3 Hash3 Hash3，它们的返回值被分别对位数组的大小（即N * _X）取模，得到三个不同的哈希值 h a s h 1 hash1 hash1、 h a s h 2 hash2 hash2和 h a s h 3 hash3 hash3。这样可以使得每个元素在位数组中的位置更加分散，减少冲突的可能性。

最后，使用bitset的set函数将对应的位设置为1，表示该元素存在于集合中。

2. 查找

在C++中，布隆过滤器的查找操作可以通过以下方式实现：

bool contains(const K& key) const {
    size_t len = N * _X;
    size_t hash1 = Hash1()(key) % len;
    size_t hash2 = Hash2()(key) % len;
    size_t hash3 = Hash3()(key) % len;

    // 判断位数组中对应位置的值是否都为1
    if (_bs.test(hash1) && _bs.test(hash2) && _bs.test(hash3)) {
        return true;  // 可能存在于集合中
    }

    return false;  // 一定不存在于集合中
}

在上述代码中，contains函数接受一个键值key作为参数，通过哈希函数将其映射到位数组中的多个位置。然后，使用bitset的test函数判断位数组中对应位置的值是否都为1。如果所有对应的位都是1，则返回true，表示该元素可能存在于集合中；否则，返回false，表示该元素一定不存在于集合中。

需要注意的是，由于布隆过滤器存在一定的误判率，即有可能将一个不存在的元素误判为存在，因此在使用contains函数进行查询时，可能会出现误判的情况。因此，布隆过滤器更适合用于快速判断元素不存在的情况，而不能完全依赖它来判断元素是否存在。

3. 删除（不支持）

🚨🚨布隆过滤器不能直接支持删除工作，因为在删除一个元素时，可能会影响其他元素

💧布隆过滤器使用多个哈希函数将元素映射到位数组中的多个位置，并将这些位置的位设置为1。在查询操作时，如果所有位置的位都为1，则判断该元素可能存在于集合中。然而，当我们想要删除一个元素时，如果直接将对应位置的位设置为0，那么其他元素可能会受到影响。

💧考虑这样一种情况：假设有两个元素A和B，它们经过多个哈希函数映射后，分别在位数组的位置1、2、3上都设置了1。现在我们想要删除元素A，将位置1、2、3上的位设置为0。但是，这样一来，当查询元素B时，由于位置1、2、3上的位都为0，系统会错误地判断元素B不存在于集合中，即产生了误判。

💧因此，为了避免删除操作对其他元素的判断造成干扰，布隆过滤器通常被设计为只能进行插入和查询操作，不支持删除操作。如果需要删除某个元素，通常的做法是重新构建一个新的布隆过滤器，将需要删除的元素排除在外。

C++模拟实现布隆过滤器

#include <vector>
#include <string>
#include <time.h>
using namespace std;

    //位图
template<size_t N>
class bitset
{
public:
	bitset()
	{
		_bits.resize(N / 8 + 1, 0);
	}

	void set(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;
		_bits[i] |= (1 << j);
	}

	void reset(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;

		_bits[i] &= ~(1 << j);
	}

	bool test(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;

		return _bits[i] & (1 << j);
	}

private:
	vector<char> _bits;
};


struct BKDRHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (auto ch : s)
		{
			hash += ch;
			hash *= 31;
		}

		return hash;
	}
};

struct APHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (long i = 0; i < s.size(); i++)
		{
			size_t ch = s[i];
			if ((i & 1) == 0)
			{
				hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
			}
			else
			{
				hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
			}
		}
		return hash;
	}
};


struct DJBHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 5381;
		for (auto ch : s)
		{
			hash += (hash << 5) + ch;
		}
		return hash;
	}
};

// N最多会插入key数据的个数
template<size_t N,
	class K = string,
	class Hash1 = BKDRHash,
	class Hash2 = APHash,
	class Hash3 = DJBHash>
class BloomFilter            //布隆过滤器
{
public:
	void set(const K& key)
	{
		size_t len = N * _X;
		size_t hash1 = Hash1()(key) % len;
		_bs.set(hash1);

		size_t hash2 = Hash2()(key) % len;
		_bs.set(hash2);

		size_t hash3 = Hash3()(key) % len;
		_bs.set(hash3);

		//cout << hash1 << " " << hash2 << " " << hash3 << " " << endl << endl;
	}

	bool test(const K& key)
	{
		size_t len = N * _X;

		size_t hash1 = Hash1()(key) % len;
		if (!_bs.test(hash1))
		{
			return false;
		}

		size_t hash2 = Hash2()(key) % len;
		if (!_bs.test(hash2))
		{
			return false;
		}

		size_t hash3 = Hash3()(key) % len;
		if (!_bs.test(hash3))
		{
			return false;
		}

		// 在      不准确的，存在误判
		// 不在    准确的

		return true;
	}
private:
	static const size_t _X = 6;
	bitset<N* _X> _bs;
};

四、布隆过滤器的优缺点

✅优点

  1. 快速查询：布隆过滤器可以在常数时间内进行元素的插入和查询操作，不受数据规模的影响。这是因为布隆过滤器使用位数组和多个哈希函数，可以快速计算出元素对应的位数组位置，并进行位操作。

  2. 空间效率高：相比于其他数据结构，布隆过滤器占用的空间很小。它通过位数组来表示元素的存在与否，并且可以通过调整位数组大小和哈希函数个数来控制空间占用和误判率之间的平衡。

  3. 高效的哈希函数：布隆过滤器使用多个哈希函数将元素映射到位数组中的多个位置，这样可以减少冲突的可能性，提高查询的准确性。

✅缺点

  1. 误判率：布隆过滤器存在一定的误判率，即有可能将一个不存在的元素误判为存在。这是由于位数组中的某些位置可能被多个元素映射到，导致多个元素的位都被设置为1。因此，在实际使用中，需要根据需求和误判率的可接受范围来选择合适的位数组大小和哈希函数个数。

  2. 不支持删除操作：布隆过滤器的设计初衷是用于快速判断元素是否存在，而不支持删除操作。因为删除一个元素可能会影响其他元素的判断结果。如果需要支持删除操作，可以考虑使用其他数据结构或者扩展布隆过滤器的设计。

  3. 无法存储额外信息：布隆过滤器只能判断元素是否存在，无法存储额外的信息。如果需要存储额外的信息，可以考虑使用其他数据结构，如哈希表或数据库。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1154772.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

动作捕捉系统输出四元数、欧拉角数据

动作捕捉系统输出四元数、欧拉角数据

四元数和欧拉角是进行无人机、无人车、机器人等相关实验中经常需要获取的数据。NOKOV度量动作捕捉系统支持实时获取数据&#xff0c;也支持采集导出数据。 一、创建刚体 1、在场地中间放置被测物&#xff0c;这时被测物显示在形影软件界面中。 2、在形影软件界面左上角点击“…
阅读更多...
银河集团香港优才计划95分获批案例展示！看看是如何申请的？

银河集团香港优才计划95分获批案例展示！看看是如何申请的？

银河集团香港优才计划95分获批案例展示&#xff01;看看是如何申请的&#xff1f; 今天来分享一则银河集团香港优才计划获批案例&#xff01;客户本科学历非名校、从事业务支援及人力资源行业&#xff0c;优才打分95分&#xff0c;这个条件可能在很多人的印象里&#xff0c;会觉…
阅读更多...
C语言实现从键盘输入一个正整数，判断他们是否是回文数，所谓回文数，是指正数和反数都一样例如 123321 是回文数

C语言实现从键盘输入一个正整数，判断他们是否是回文数，所谓回文数，是指正数和反数都一样例如 123321 是回文数

完整代码&#xff1a; /*从键盘输入一个正整数&#xff0c;判断他们是否是回文数&#xff0c;所谓回文数&#xff0c;是指正数和反数都一样 例如 123321 是回文数*/ #include<stdio.h> //这个数的最大长度 #define N 10 int main(){//length是这个数的长度int num,lengt…
阅读更多...
CDN加速技术海外与大陆优劣势对比

CDN加速技术海外与大陆优劣势对比

内容分发网络&#xff08;CDN&#xff09;是一项广泛应用于网络领域的技术&#xff0c;旨在提高网站和应用程序的性能、可用性和安全性。CDN是一种通过将内容分发到全球各地的服务器来加速数据传输的服务。本文将探讨使用CDN的优势以及国内CDN和海外CDN之间的不同优势和劣势。 …
阅读更多...
驱动第十天

驱动第十天

阅读更多...
智能化管理大规模电脑文件的高效方法

智能化管理大规模电脑文件的高效方法

在现代社会中&#xff0c;电脑已经成为我们生活和工作中必不可少的工具。随着时间的推移&#xff0c;我们电脑中的文件越来越多&#xff0c;管理起来也变得越来越困难。为了提高工作效率&#xff0c;我们需要学会高效管理电脑文件。下面&#xff0c;我将分享一些在线分享批量智…
阅读更多...
Mysql5.7安装配置详细图文教程（msi版本）

Mysql5.7安装配置详细图文教程（msi版本）

博主介绍&#xff1a;✌全网粉丝5W&#xff0c;全栈开发工程师&#xff0c;从事多年软件开发&#xff0c;在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战&#xff0c;博主也曾写过优秀论文&#xff0c;查重率极低&#xff0c;在这方面有丰富的经验…
阅读更多...
超级账本区块链Fabric2.4.4版本搭建过程（完整过程）

超级账本区块链Fabric2.4.4版本搭建过程（完整过程）

前提环境:乌班图20.04环境 安装所需要的工具 先配置一下代理源为阿里云代理&#xff1a; sudo apt-get update 更新源 sudo apt-get install ssh 安装远程客户端 sudo apt-get install curl 安装命令行工具 sudo apt-get install git 安装git sudo apt-get install gcc 安装…
阅读更多...
C语言之用指针交换两个数

C语言之用指针交换两个数

1.指针存放是是地址&#xff0c;所以在用指针交换两个数的时候&#xff0c;需要对指针进行解引用(*p)。 用指针交换两个数&#xff0c;需要知道p1p2与*p1*p2。 p1p1是将p2的值赋值给p1. *p1*p2是将p2指针地址存放的值&#xff0c;赋值给p1指针地址存放的值&#xff0c;即p1地…
阅读更多...
YOLOv7改进： AIFI (尺度内特征交互）助力YOLO | YOLO终结者？RT-DETR一探究竟

YOLOv7改进： AIFI (尺度内特征交互）助力YOLO | YOLO终结者？RT-DETR一探究竟

💡💡💡本文全网首发独家改进： AIFI (尺度内特征交互）助力YOLO ,提升尺度内和尺度间特征交互能力，同时降低多个尺度的特征之间进行注意力运算，计算消耗较大等问题 推荐指数：五星 AIFI | 亲测在多个数据集能够实现涨点 收录： YOLOv7高阶自研专栏介绍： http:…
阅读更多...
JSX语法入门

JSX语法入门

目录 元素与组件 属性与表达式 条件渲染 列表渲染 使用JSX的注意事项 总结 JSX是JavaScript的扩展语法&#xff0c;它允许我们在JavaScript中编写类似HTML的代码。在React中广泛使用JSX来描述用户界面。在本文中&#xff0c;我们将介绍JSX的基础知识&#xff0c;包括元素…
阅读更多...
CSDN----Markdown编辑器

CSDN----Markdown编辑器

这里写自定义目录标题 欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题&#xff0c;有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants 创建一个自定义列表如何创建一个…
阅读更多...
库函数sort

库函数sort

1 sort自定义大小cmp bool cmp(Rec a,Rec b)//W1a是否应该排在b前面 { return a.x<b.x;//a小于b就排在前面 // return a>b; }只需在这里改变大于还是小于排序 #include <iostream> #include <algorithm> #include <vector> #include <cti…
阅读更多...
脉冲离子风机和普通离子风机有什么区别

脉冲离子风机和普通离子风机有什么区别

脉冲离子风机和普通离子风机都是利用电离空气的原理来净化空气中的微粒和有害气体&#xff0c;但它们的工作原理和性能有所不同。 普通离子风机是通过将电压施加到电极上&#xff0c;使电极周围的空气分子电离&#xff0c;产生负离子&#xff0c;从而吸附空气中的微粒和有害气体…
阅读更多...
react中的useReducer复杂的状态管理

react中的useReducer复杂的状态管理

reducer官网教程 useReducer 是 React 提供的一个用于状态管理的 Hook。它可以替代 useState&#xff0c;更适用于处理复杂的状态逻辑。 useReducer 接受一个reducer函数和一个初始状态&#xff0c;并返回当前状态以及一个 dispatch 函数&#xff0c;用来触发状态更新。reduce…
阅读更多...
vue/react项目刷新页面出现404报错的原因及解决办法

vue/react项目刷新页面出现404报错的原因及解决办法

Vue项目打包部署到线上后,刷新页面会提示404,下面这篇文章主要给大家介绍了关于vue/react项目刷新页面出现404报错的原因及解决办法,文中将解决的办法介绍的很详细,需要的朋友可以参考下 ​​​​​​​ 背景解决办法 法1&#xff1a;将vue/react路由模式由history路由改为has…
阅读更多...
c++-set和map

c++-set和map

文章目录 前言一、set容器1、set容器介绍2、set的使用2.1 set的构造函数和迭代器2.2 set的容量2.3 set修改操作 3、multiset容器3.1 multiset容器介绍3.2 multiset容器使用 二、map容器1、map容器介绍2、map容器使用2.1 map的构造函数与迭代器2.2 map中元素的修改2.3 map的容量…
阅读更多...
ME创新计划 | 山乡花开项目护童计划——山乡宝贝周末营会

ME创新计划 | 山乡花开项目护童计划——山乡宝贝周末营会

为给山乡宝贝搭建更大的平台&#xff0c;帮助他们探索自身的潜力&#xff0c;并培养自信和自尊。2023年10月28日至29日&#xff0c;溆浦志愿者协会开展“ME创新计划 | 山乡宝贝项目护童计划——山乡宝贝周末营会”活动&#xff0c;来自卢峰镇、桥江镇、大江口镇等35名山乡宝贝参…
阅读更多...
代购商城源码如何保障用户信息和交易数据的安全性？

代购商城源码如何保障用户信息和交易数据的安全性？

多样支付方式的需求和背景 支付方式的重要性 随着电子商务的快速发展&#xff0c;支付是在线购物过程中至关重要的环节。不同用户有着不同的支付习惯和需求&#xff0c;因此一个代购商城源码需要支持多种支付方式&#xff0c;以满足用户的个性化需求。 便捷性和安全性的需求 支…
阅读更多...
Anaconda安装Bertopic流程

Anaconda安装Bertopic流程

前面是参考一个博主的搭建&#xff0c;但是我装之后还是遇到了些问题 1、先建一个虚拟环境 conda create --name BERTopic_Env python3.8 activate BERTopic_Env2、安装清华镜像 conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ con…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023