dfs序及相关例题

news2025/1/16 8:10:14

常用的三种dfs序

欧拉序

每经过一次该点记录一次的序列。

dfs序

记录入栈和出栈的序列。

dfn序

只记录入栈的序列。

dfs序

DFS 序列是指 DFS 调用过程中访问的节点编号的序列。

在这里插入图片描述

如何求dfs序？可以用以下代码来找dfs序。

    vector<vector<int>> g(n+1);
    for(int i = 1; i < n; ++i) {
        // u,v 建图
        int u,v; u = fread(); v = fread();
        g[u].push_back(v);
        g[v].push_back(u);
    }
    // dfs序的左右端点
    // 表示以x为根的子树的左右端点位置
    vector<int> l(n + 1), r(n + 1);
    int cnt = 0;
    // 一个dfs找dfs序
    auto dfs = [&](auto &&self, int u, int fa) -> void {
        l[u] = ++cnt;
        for(auto y: g[u]) {
            if(y == fa) continue;
            self(self, y,u);
        }
        r[u] = cnt;
    };
    dfs(dfs, k,-1);

一道简单的dfs序的问题。

题目链接：求和 (nowcoder.com)

问题描述：n个节点，n - 1条边，根节点为k。现在又m个操作。

1 a x：将节点a的权值加上x
2 a：求a节点的子树上所有节点的和（包括a节点本身）

思路，发现以a为根的子树权值和是一个非线性的，不能用树状数组或者线段树来做。但是dfs序却有一个天然的顺序可以来处理。

在这里插入图片描述

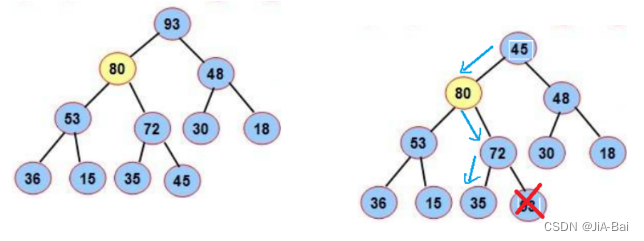
观察上图：

以5为根的子树序列在dfs序中的排序是：1 2 3 4 5 6 7 8
以8为根的子树序列在dfs序中的排序是：2 3
以2为根的子树序列在dfs序中的排序是：3
以1为根的子树序列在dfs序中的排序是：4 5 6 7 8

…

我们发现，每个子树都对应 DFS 序列中的连续一段（一段区间）。

DFS（图论） - OI Wiki (oi-wiki.org)

因此本题思路就是：用dfs序将非序列顺序转线性序列。之后就是单点修改，区间查询，可以用树状数组或者线段树来进行求解。

本人是用线段树来进行处理的（线段树大法好

AC代码：

#include <iostream>
#include <vector>
#include <string>
#include <cstring>
#include <set>
#include <map>
#include <queue>
#include <ctime>
#include <random>
#include <sstream>
#include <numeric>
#include <stdio.h>
#include <functional>
#include <bitset>
#include <algorithm>
using namespace std;

// #define Multiple_groups_of_examples
#define int_to_long_long
#define IOS std::cout.tie(0);std::cin.tie(0)->sync_with_stdio(false); // 开IOS，需要保证只使用Cpp io流 *
#define dbgnb(a) std::cout << #a << " = " << a << '\n';
#define dbgtt cout<<" !!!test!!! "<<'\n';
#define rep(i,x,n) for(int i = x; i <= n; i++)

#define all(x) (x).begin(),(x).end()
#define pb push_back
#define vf first
#define vs second

typedef long long LL;
#ifdef int_to_long_long
#define int long long
#endif
typedef pair<int,int> PII;

const int INF = 0x3f3f3f3f;
const int N = 2e5 + 21;


struct SegTree {
    static const int N = 1e6 + 21;
    struct node {
        int l, r, mi;
        LL sum,add;
    }tr[N << 2];
    int w[N];
    // 左子树
    inline int ls(int p) {return p<<1; }
    // 右子树
    inline int rs(int p) {return p<<1|1; }
    // 向上更新
    void pushup(int u) {
        tr[u].sum = tr[ls(u)].sum + tr[rs(u)].sum;
        tr[u].mi = min(tr[ls(u)].mi, tr[rs(u)].mi);
    }
    // 向下回溯时，先进行更新
    void pushdown(int u) { // 懒标记，该节点曾经被修改，但其子节点尚未被更新。
        auto &root = tr[u], &right = tr[rs(u)], &left = tr[ls(u)];
        if(root.add) {
            right.add += root.add; right.sum += (LL)(right.r - right.l + 1)*root.add; right.mi -= root.add;
            left.add += root.add; left.sum += (LL)(left.r - left.l + 1)*root.add; left.mi -= root.add;
            root.add = 0;
        }

    }
    // 建树
    void build(int u, int l, int r) {
        if(l == r) tr[u] = {l, r, w[r], w[r], 0};
        else {
            tr[u] = {l,r}; // 容易忘
            int mid = l + r >> 1;
            build(ls(u), l, mid), build(rs(u), mid + 1, r);
            pushup(u);
        }
    }
    // 修改
    void modify(int u, int l, int r, int d) {
        if(tr[u].l >= l && tr[u].r <= r) {
            tr[u].sum += (LL)(tr[u].r - tr[u].l + 1)*d;
            tr[u].add += d;
        }
        else {
            pushdown(u);
            int mid = tr[u].l + tr[u].r >> 1;
            if(l <= mid) modify(ls(u), l ,r, d);
            if(r > mid) modify(rs(u), l, r, d);
            pushup(u);
        }
    }
    // 查询
    LL query(int u, int l, int r) {
        if(tr[u].l >= l && tr[u].r <= r) {
            return tr[u].sum;
        }
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        LL sum = 0;
        if(l <= mid) sum = query(ls(u), l, r);
        if(r > mid ) sum += query(rs(u), l, r);
        return sum;
    }
}tree;
// 当输入数据大于 1e6 时用快读
inline int fread() // 快读
{
    int x = 0, f = 1; char ch = getchar();
    while(ch < '0' || ch > '9') {if (ch == '-') f = -1; ch = getchar(); }
    while(ch >= '0' && ch <= '9') {
        x = x * 10 + (ch - '0');
        ch = getchar();
    }
    return x * f;
}
void inpfile();
void solve() {
    // int n,m,k; cin>>n>>m>>k;
    int n = fread(), m = fread(), k = fread();
    vector<int> a(n + 1);
    for(int i = 1; i <= n; ++i) a[i] = fread();
    vector<vector<int>> g(n+1);
    for(int i = 1; i < n; ++i) {
        int u,v; u = fread(); v = fread();
        g[u].push_back(v);
        g[v].push_back(u);
    }
    vector<int> l(n + 1), r(n + 1);
    int cnt = 0;
    auto dfs = [&](auto &&self, int u, int fa) -> void {
        l[u] = ++cnt;
        for(auto y: g[u]) {
            if(y == fa) continue;
            self(self, y,u);
        }
        r[u] = cnt;
    };
    dfs(dfs, k,-1);
    for(int i = 1; i <= n; ++i) tree.w[l[i]] = a[i];
    tree.build(1,1,n);
    while(m--) {
        int opt,x,y; opt = fread();
        if(opt == 2) {
            // cin>>x>>y;
            x = fread();
            cout<<tree.query(1, l[x], r[x])<<'\n';
        } else {
            x = fread(), y = fread();
            tree.modify(1,l[x],l[x],y);
        }
    }
}
#ifdef int_to_long_long
signed main()
#else
int main()
#endif

{
    #ifdef Multiple_groups_of_examples
    int T; cin>>T;
    while(T--)
    #endif
    solve();
    return 0;
}
void inpfile() {
    #define mytest
    #ifdef mytest
    freopen("ANSWER.txt", "w",stdout);
    #endif
}