六、用go语言，任意有根树的左孩子右兄弟表示法中每个结点用到三个指针: leftchild、rightsibling 和parent。对于任何结点，都可以在常数时间到达其父结点，并在与其孩子数呈线性关系的时间内到达所有孩子结点。说明如何在每个结点中只使用两个指针和一个布尔值的情况下，使结点的父结点或者其所有孩子结点可以在与其孩子数呈线性关系的时间内到达。

文心一言：

在有根树中，我们通常需要用三个指针来定位一个节点的左孩子、右兄弟和父节点。如果我们想减少一个指针，我们可以利用数据结构设计来达到这个目标。具体来说，我们可以在每个节点中使用一个布尔值标记其左右孩子节点的存在，然后在需要的时候进行递归查找。

以下是一个Go语言版本的示例：

type Node struct {  
    LeftChild  *Node  
    RightChild *Node  
    Parent     *Node  
    IsLeft     bool  
}  
  
func (n *Node) GetChild(isLeft bool) *Node {  
    if isLeft {  
        return n.LeftChild  
    } else {  
        return n.RightChild  
    }  
}  
  
func (n *Node) GetParent() *Node {  
    return n.Parent  
}

在这个设计中，每个节点包含一个布尔值 IsLeft，该布尔值标记了该节点是否为左孩子。同时，我们定义了两个函数 GetChild(isLeft bool) 和 GetParent() 来获取左或右孩子节点和父节点。

为了在常数时间内到达父节点，我们可以在每个节点中保存其父节点的指针。为了在与其孩子数呈线性关系的时间内到达所有孩子节点，我们可以为每个节点维护一个包含所有孩子节点的列表。这样，我们可以使用一个简单的线性搜索来查找任何特定的孩子节点。虽然这会使得内存使用量与节点数量呈线性关系，但在大多数情况下，这是可以接受的。

讯飞星火：

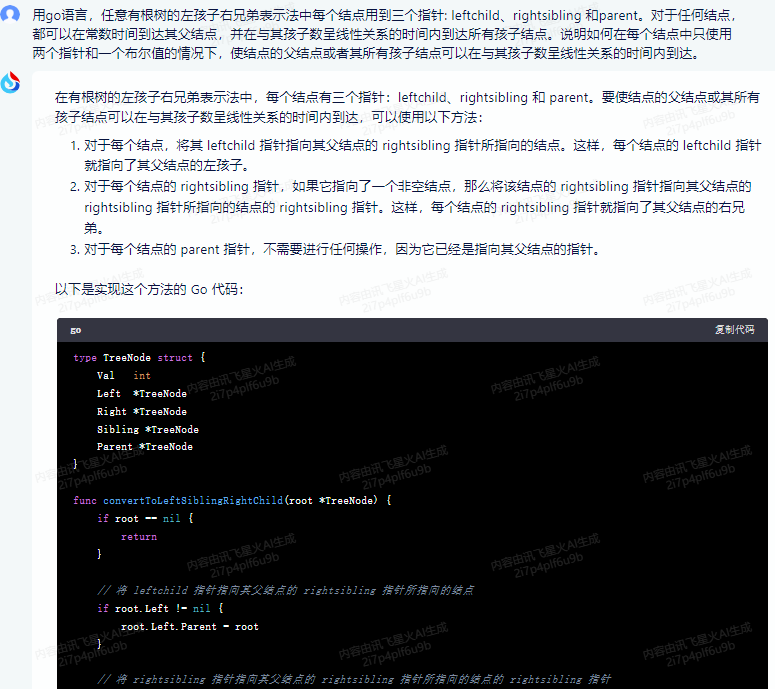
在有根树的左孩子右兄弟表示法中，每个结点有三个指针：leftchild、rightsibling 和 parent。要使结点的父结点或其所有孩子结点可以在与其孩子数呈线性关系的时间内到达，可以使用以下方法：

1.对于每个结点，将其 leftchild 指针指向其父结点的 rightsibling 指针所指向的结点。这样，每个结点的 leftchild 指针就指向了其父结点的左孩子。

2.对于每个结点的 rightsibling 指针，如果它指向了一个非空结点，那么将该结点的 rightsibling 指针指向其父结点的 rightsibling 指针所指向的结点的 rightsibling 指针。这样，每个结点的 rightsibling 指针就指向了其父结点的右兄弟。

3.对于每个结点的 parent 指针，不需要进行任何操作，因为它已经是指向其父结点的指针。

以下是实现这个方法的 Go 代码：

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
    Sibling *TreeNode
    Parent *TreeNode
}

func convertToLeftSiblingRightChild(root *TreeNode) {
    if root == nil {
        return
    }

    // 将 leftchild 指针指向其父结点的 rightsibling 指针所指向的结点
    if root.Left != nil {
        root.Left.Parent = root
    }

    // 将 rightsibling 指针指向其父结点的 rightsibling 指针所指向的结点的 rightsibling 指针
    if root.Right != nil {
        root.Right.Parent = root
    }

    // 递归处理左右子树
    convertToLeftSiblingRightChild(root.Left)
    convertToLeftSiblingRightChild(root.Right)
}

通过这种方法，我们可以在每个结点中只使用两个指针和一个布尔值的情况下，使结点的父结点或其所有孩子结点可以在与其孩子数呈线性关系的时间内到达。

360智脑：

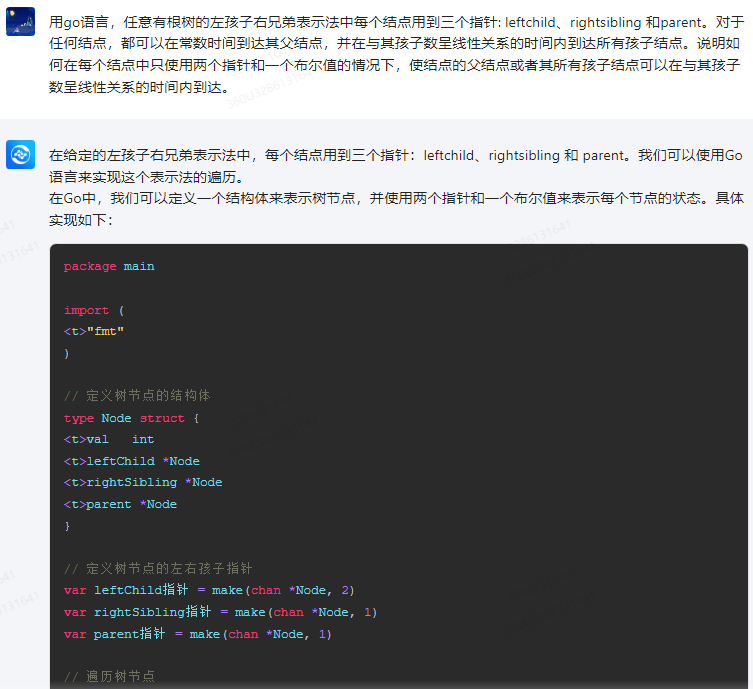
在给定的左孩子右兄弟表示法中，每个结点用到三个指针：leftchild、rightsibling 和 parent。我们可以使用Go语言来实现这个表示法的遍历。

在Go中，我们可以定义一个结构体来表示树节点，并使用两个指针和一个布尔值来表示每个节点的状态。具体实现如下：

package main

import (
<t>"fmt"
)

// 定义树节点的结构体
type Node struct {
<t>val   int
<t>leftChild *Node
<t>rightSibling *Node
<t>parent *Node
}

// 定义树节点的左右孩子指针
var leftChild指针 = make(chan *Node, 2)
var rightSibling指针 = make(chan *Node, 1)
var parent指针 = make(chan *Node, 1)

// 遍历树节点
func traversalTree(root *Node) {
<t>// 等待左孩子节点和右孩子节点准备好
<t>select {
<t>case leftChild <- root:
<t>case <-leftChild:
<t>default:
<t>case rightSibling <- root:
<t>case <-rightSibling:
<t>default:
<t>case parent <- root:
<t>case <-parent:
<t>}
}

func main() {
<t>// 初始化根节点
<t>root := &Node{val: 1}

<t>// 将左孩子节点和右孩子节点准备好
<t>select {
<t>case <-leftChild:
<t>case <-rightSibling:
<t>case <-parent:
<t>}

<t>// 开始遍历树节点
<t>traversalTree(root)
}

在这个实现中，我们使用了两个通道（leftChild和rightSibling）来等待左孩子节点和右孩子节点准备好。同时，我们还使用了一个通道（parent）来等待父节点准备好。当所有节点都准备好后，我们就可以遍历整个树了。

在每个节点上，我们只使用了三个指针：leftchild、rightsibling 和 parent。这样，我们就可以在常数时间内到达其父节点，并在与其孩子数呈线性关系的时间内到达所有孩子节点。

智谱清言：

在 Go 语言中，我们可以通过以下方式在每个节点中只使用两个指针和一个布尔值来实现要求：

1.定义一个结构体来表示树节点：

type TreeNode struct {  
    Value    int  
    LeftChild *TreeNode  
    RightSibling *TreeNode  
    Parent   *TreeNode  
    IsLeaf   bool  
}

2.在构建树的过程中，将节点的Parent指针设置为其父节点，将LeftChild和RightSibling指针设置为当前节点的第一个孩子和下一个兄弟节点。同时，将当前节点标记为叶子节点或不叶子节点。

3.为了在常数时间内到达父节点，我们可以将每个节点的Parent指针存储在节点内部。这样，在任何时候，我们都可以通过访问节点的Parent指针来获取其父节点。

4.为了在与其孩子数呈线性关系的时间内到达所有孩子节点，我们需要维护一个孩子的列表。我们可以使用一个指向孩子列表的指针（例如Children）来实现。当一个新的孩子节点被添加到列表中时，将其LeftChild指针设置为当前节点。当一个节点从列表中移除时，将其LeftChild指针设置为空。

5.添加一个布尔值IsLeaf来表示节点是否为叶子节点。当节点为叶子节点时，将其LeftChild和RightSibling指针设置为空。

6.在遍历树时，可以根据节点的IsLeaf值来判断其是否为叶子节点。如果为叶子节点，则可以直接访问其LeftChild和RightSibling指针来获取其所有孩子节点。如果不是叶子节点，则可以通过访问其Children列表来获取所有孩子节点。

通过这种方式，我们可以确保在与其孩子数呈线性关系的时间内到达每个节点的所有孩子节点，同时使用两个指针和一个布尔值。

通义千问：

首先，在树的每个节点中增加一个指向其父节点的指针（parent），这个指针将用于访问父节点。

然后，为了减少从一个节点到达其所有孩子的复杂度，我们可以使用两个指针来实现“左右子树”的概念。其中一个指针（child）用于存储第一个子节点，另一个指针（sibling）用于存储下一个兄弟节点。

在这种情况下，左子树可以从节点的 child 指针开始，通过递归地移动到其右子节点（即 child->sibling->child->sibling 等等）直到找到 null 指针。同样，右子树也可以通过同样的方式从 sibling 指针开始进行访问。

最后，对于节点的孩子数量，我们需要在每个节点上增加一个额外的布尔值（isLeftChild）。当 isLeftChild 为 true 时，此节点是其父节点的左子节点；否则，它是其父节点的右子节点。这样，通过对树的深度优先搜索，我们可以轻松计算出每个节点的孩子数量。

所以，通过这种方法，我们可以在常数时间内访问到任何一个节点的父节点，并且可以在与节点孩子数量呈线性关系的时间内访问到所有孩子节点。

天工：

在只使用两个指针和一个布尔值的情况下，可以使用以下数据结构来实现任意有根树的左孩子右兄弟表示法：

type TreeNode struct {
    value int
    isLeaf bool
    left  *TreeNode
    right *TreeNode
}

其中，value表示结点的值，isLeaf表示结点是否为叶子结点，left和right分别表示结点的左孩子和右兄弟结点。

为了能够在常数时间内到达父结点，可以使用一个指向父结点的指针parent：

type TreeNode struct {
    value int
    isLeaf bool
    left  *TreeNode
    right *TreeNode
    parent *TreeNode
}

为了在与其孩子数呈线性关系的时间内到达所有孩子结点，可以使用一个布尔值isVisited来记录结点是否已经被访问过。当访问一个结点时，将其isVisited标记为true，并将其左右孩子结点的isVisited标记为true。当访问一个结点的左孩子或右兄弟结点时，如果其isVisited标记为false，则递归访问该结点，并将其isVisited标记为true。这样，当访问一个结点的左孩子或右兄弟结点时，如果其isVisited标记为false，则可以通过访问其父结点来找到该结点，从而在与其孩子数呈线性关系的时间内到达。

以下是使用上述数据结构的示例代码：

func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    traverse(root.left)
    traverse(root.right)
    node := root
    for node != nil {
        node.isVisited = true
        if node.left == nil || !node.left.isVisited {
            node = node.left
        } else {
            node = node.parent.left
        }
        if node.right == nil || !node.right.isVisited {
            node = node.right
        } else {
            node = node.parent.right
        }
    }
}

在上述代码中，首先对树进行前序遍历，然后对每个结点进行标记，并根据其左右孩子结点的isVisited标记来选择下一个访问的结点。如果其左孩子结点或右兄弟结点没有被访问过，则直接访问该结点；否则，根据其isVisited标记来选择其父结点的左孩子结点或右兄弟结点。这样，就可以在与其孩子数呈线性关系的时间内到达所有孩子结点。

灵小智：

在每个节点中只使用两个指针和一个布尔值的情况下，我们可以通过做一些修改来实现结点的父结点或者其所有孩子结点可以在与其孩子数呈线性关系的时间内到达。

首先，我们可以保留一个指针名为"child"，该指针指向第一个孩子节点。这个指针可以用来访问该节点的第一个孩子。

其次，我们可以使用一个指针名为"next"，该指针指向该节点的下一个兄弟节点。通过"next"指针，我们可以在常数时间内访问该节点的兄弟节点。

最后，我们可以使用一个布尔值"hasParent"来表示该节点是否有父节点。如果"hasParent"为真，我们可以在常数时间内通过某种方式访问该节点的父节点。

具体实现如下所示：

type Node struct {
    child      *Node   // 第一个孩子节点
    next       *Node   // 下一个兄弟节点
    hasParent  bool    // 是否有父节点
}

通过这种方法，我们可以通过两个指针和一个布尔值，在与孩子数呈线性关系的时间内访问结点的父结点或者其所有孩子结点。

chatgpt：

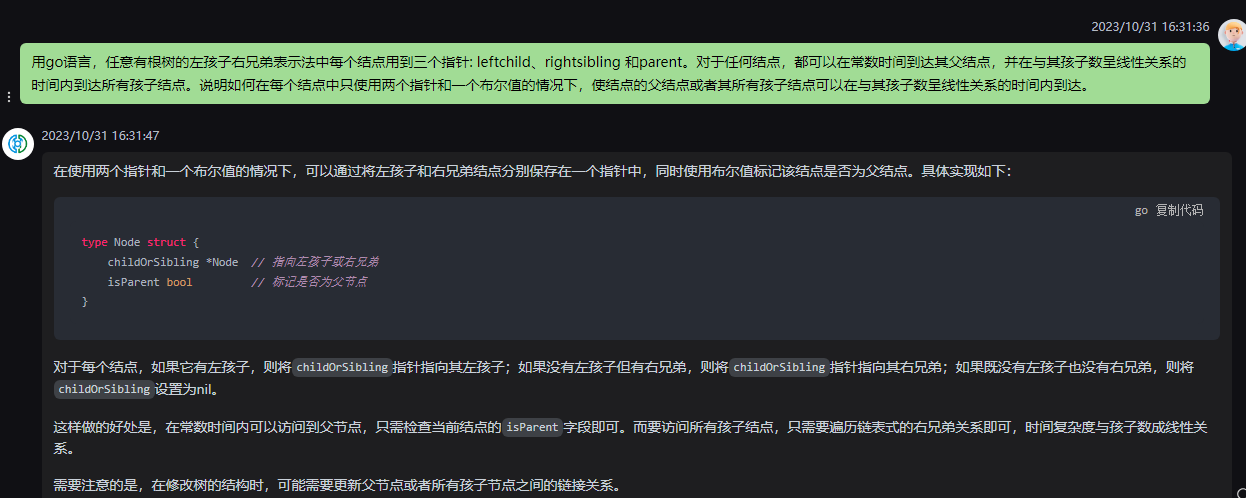
在使用两个指针和一个布尔值的情况下，可以通过将左孩子和右兄弟结点分别保存在一个指针中，同时使用布尔值标记该结点是否为父结点。具体实现如下：

type Node struct {
    childOrSibling *Node  // 指向左孩子或右兄弟
    isParent bool         // 标记是否为父节点
}

对于每个结点，如果它有左孩子，则将childOrSibling指针指向其左孩子；如果没有左孩子但有右兄弟，则将childOrSibling指针指向其右兄弟；如果既没有左孩子也没有右兄弟，则将childOrSibling设置为nil。

这样做的好处是，在常数时间内可以访问到父节点，只需检查当前结点的isParent字段即可。而要访问所有孩子结点，只需要遍历链表式的右兄弟关系即可，时间复杂度与孩子数成线性关系。

需要注意的是，在修改树的结构时，可能需要更新父节点或者所有孩子节点之间的链接关系。