题目
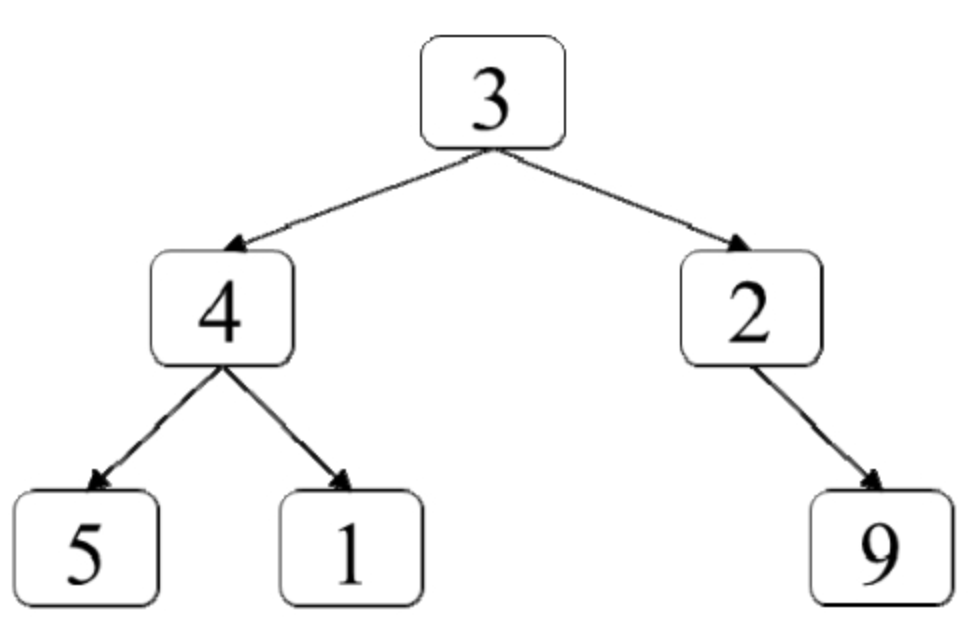
输入一棵二叉树,请找出二叉树中每层的最大值。例如,输入图7.4中的二叉树,返回各层节点的最大值[3,4,9]。
分析:用一个队列实现二叉树的广度优先搜索
由于要找出二叉树中每层的最大值,因此在遍历时需要知道每层什么时候开始、什么时候结束。如果还是和前面一样只用一个队列来保存尚未遍历到的节点,那么有可能位于不同的两层的节点同时在队列之中。例如,遍历到节点4时,就把节点4从队列中取出来,此时节点2已经在队列中。接下来要把节点4的两个子节点(节点5和节点1)都添加到队列中。这个时候第2层的节点2和第3层的节点5、节点1都在队列中。
如果不同层的节点同时位于队列之中,那么每次从队列之中取出节点来遍历时就需要知道这个节点位于哪一层。解决这个问题的一个办法是计数。需要注意的是,当遍历某一层的节点时,会将下一层的节点也放入队列中。因此,可以用两个变量分别记录两层节点的数目,变量current记录当前遍历这一层中位于队列之中节点的数目,变量next记录下一层中位于队列之中节点的数目。
解:用一个队列实现二叉树的广度优先搜索
public class Test {
public static void main(String[] args) {
TreeNode node3 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node2 = new TreeNode(2);
TreeNode node5 = new TreeNode(5);
TreeNode node1 = new TreeNode(1);
TreeNode node9 = new TreeNode(9);
node3.left = node4;
node3.right = node2;
node4.left = node5;
node4.right = node1;
node2.right = node9;
List<Integer> result = largestValues(node3);
System.out.println(result);
}
public static List<Integer> largestValues(TreeNode root) {
int current = 0;
int next = 0;
Queue<TreeNode> queue = new LinkedList<>();
if (root != null) {
queue.offer(root);
current = 1;
}
List<Integer> result = new LinkedList<>();
int max = Integer.MIN_VALUE;
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
current--;
max = Math.max(max, node.val);
if (node.left != null) {
queue.offer(node.left);
next++;
}
if (node.right != null) {
queue.offer(node.right);
next++;
}
if (current == 0) {
result.add(max);
max = Integer.MIN_VALUE;
current = next;
next = 0;
}
}
return result;
}
}
分析:用两个队列实现二叉树的广度优先搜索
当遍历某一层时,会将位于下一层的子节点也插入队列中,也就是说,队列中会有位于两层的节点。可以用两个不同的队列queue1和queue2分别存放两层的节点,队列queue1中只放当前遍历层的节点,而队列queue2中只放下一层的节点。
当队列queue1被清空时,当前层的所有节点都已经被遍历完。通过比较这一层所有节点的值,就能找出这一层所有节点的最大值。在开始遍历下一层之前,把队列queue1指向队列queue2,并将队列queue2重新初始化为空的队列。重复这个过程,直到所有节点都遍历完为止。
解:用两个队列实现二叉树的广度优先搜索
public class Test {
public static void main(String[] args) {
TreeNode node3 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node2 = new TreeNode(2);
TreeNode node5 = new TreeNode(5);
TreeNode node1 = new TreeNode(1);
TreeNode node9 = new TreeNode(9);
node3.left = node4;
node3.right = node2;
node4.left = node5;
node4.right = node1;
node2.right = node9;
List<Integer> result = largestValues(node3);
System.out.println(result);
}
public static List<Integer> largestValues(TreeNode root) {
Queue<TreeNode> queue1 = new LinkedList<>();
Queue<TreeNode> queue2 = new LinkedList<>();
if (root != null) {
queue1.offer(root);
}
List<Integer> result = new LinkedList<>();
int max = Integer.MIN_VALUE;
while (!queue1.isEmpty()) {
TreeNode node = queue1.poll();
max = Math.max(max, node.val);
if (node.left != null) {
queue2.offer(node.left);
}
if (node.right != null) {
queue2.offer(node.right);
}
if (queue1.isEmpty()) {
result.add(max);
max = Integer.MIN_VALUE;
queue1 = queue2;
queue2 = new LinkedList<>();
}
}
return result;
}
}