个人主页:点我进入主页
专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶
C语言刷题 数据结构初阶
欢迎大家点赞,评论,收藏。
一起努力,一起奔赴大厂。
目录
1.前言
2.算法的效率
2.1时间复杂度
2.1.1时间复杂度的定义
2.1.2时间复杂度的表示方法
2.1.3程序的时间复杂度的例子
2.2空间复杂度
3.练习
3.1
3.2
1.前言
在前面我们学过了C语言的初阶和进阶的内容,其中有很多有意思的东西,接下俩我们开始上强度,进入我们的数据结构环节,今天主要讲解的是时间复杂度和空间复杂度,我们主要通过定义的解析,实际例子的解析来讲解,最后还会讲解一些力扣的题目。
2.算法的效率
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。(简单来说我们现在主要关注算法的时间复杂度,经常出现用空间换时间)。
2.1时间复杂度
2.1.1时间复杂度的定义
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
2.1.2时间复杂度的表示方法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶
(简单来说就是我们用o(x)的形式进行表示,x是保留程序运行次数的最高阶项,且将高阶项的系数化成1,我们常出现的时间复杂度为o(1),o(n),o(logn),o(n^2)) ;
2.1.3程序的时间复杂度的例子
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}在程序中我们运行了2N+10次,我们用大o表示法,需要去掉10和系数2,因此可以得到Func2函数的时间复杂度为O(N);
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}
printf("%d\n", count);
}在Func3函数中,我们运行了M+N次,我们用大O表示法表示,由于M和N是未知的,我们就可以直接写为O(M+N);
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}在这个程序中,我们运行了100次,100是个常数,故我们可以表示为O(1);
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
我们可以看到第一次需要运行n-1次,第二次需要运行n-2次,第n次运行0次,我们可以看到这是一个等差数列,我们根据等差数列的求和公式可以得到一共运行(n-1)*n/2次,我们根据大O表示法可以得到它的最高次为n^2故时间复杂度为O(n^2);特别注意我们写时间复杂度时不是几次循环就是n的几次方,这需要我们得到程序运行了几次,然后根据大O表示法得到程序的时间复杂度。
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n-1;
while (begin < end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid;
else
return mid;
}
return -1;
} 
我们假设运行了k次,对于最坏的情况,也就是没有找到,我们需要不断二分,直到左等于右,我们每一次二分就会少一半的数据,我们就可以得到n/2^k=1,化简后可以得到log n=k,由于我们的时间复杂度中一般都是log以2为底,所以我们可以直接写为O(log n);
long long Fac(size_t N)
{
if(0 == N)
return 1;
return Fac(N-1)*N;
}
我们可以看到,程序第一次运行时 需要F(n-1),依次这样,第n-1次时需要F(0),这时候程序的每个值就都有了,根据大O表示法我们可以得到程序的时间复杂度为O(n);
long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
} 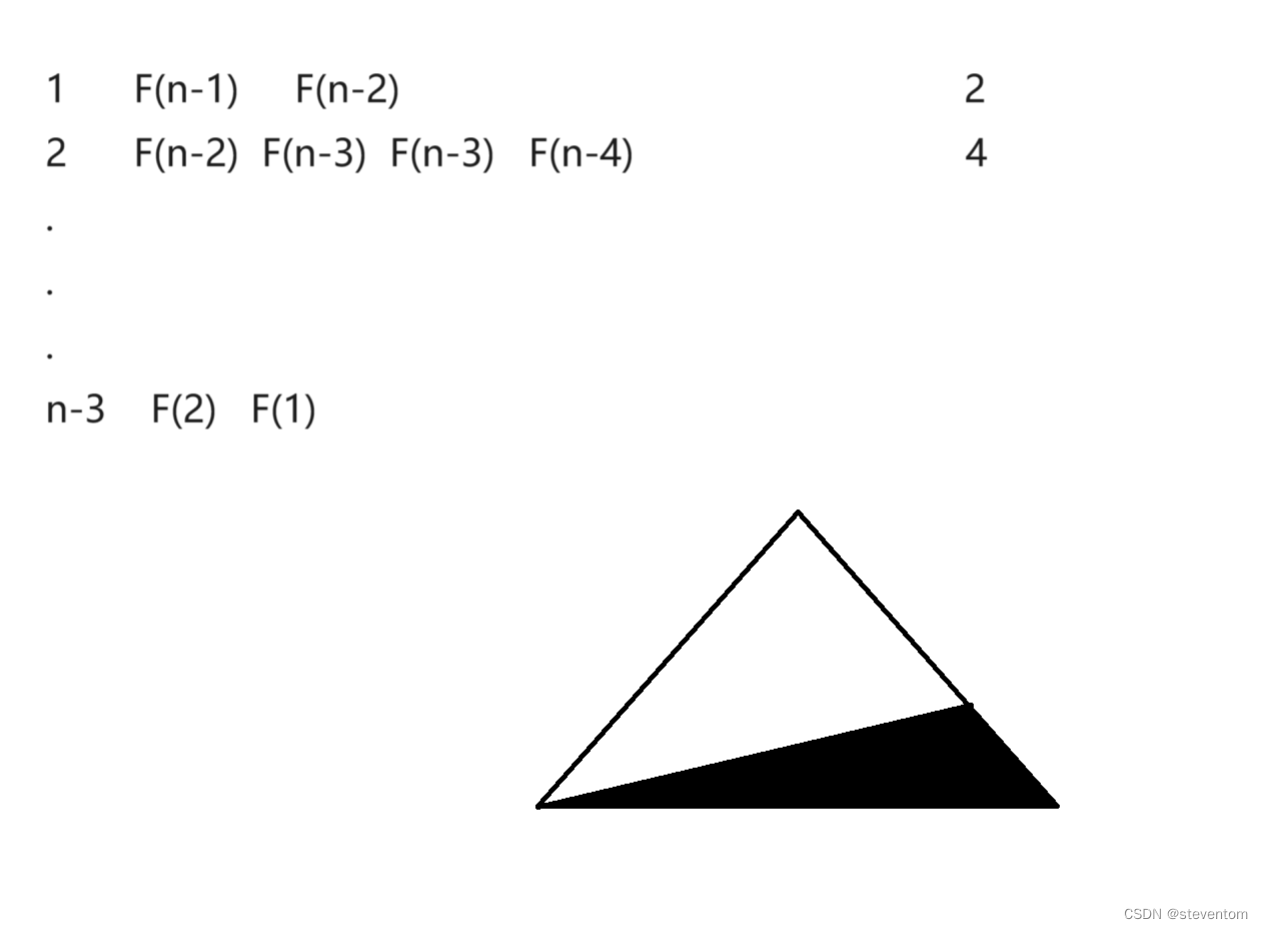
在这里我们可以近似看成等比数列,它每一次都需要2倍,故我们可以得到程序的时间复杂度为O(2^n);
2.2空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。(如果开辟常数个变量就是o(1));
int** fun(int n) {
int ** s = (int **)malloc(n * sizeof(int *));
while(n--)
s[n] = (int *)malloc(n * sizeof(int));
return s;
}我们先看**s,这里对s开辟了n个空间,再看循环里,对每个s开辟了n个空间,相当于建立了一个二维数组,故空间复杂度为O(n^2);
3.练习
3.1
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
int removeElement(int* nums, int numsSize, int val){
int i,j=0;
for(i=0;i<numsSize;i++)
{
if(nums[i]!=val)
{
nums[j++]=nums[i];
}
}
return j;
}我们每次对数据进行判断,如果数组的值和val不相等就进行赋值,相等则只有i++,这样j就是数组中元素的个数。
3.2
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
int removeDuplicates(int* nums, int numsSize){
int *p=nums,*q=nums,i,count=1;
if(numsSize>=2)
{
q++;
for(i=1;i<numsSize;i++,q++)
{
if(*p!=*q)
{
p++;
*p=*q;
count++;
}
}
}
return count;
}在这里我们用到了一个二级指针,如果数组的长度大于等于2我们进行判断,如果两个指针的内容相等只有q++,如果不相等让p++然后让q指向的数据覆盖到p指向的内容,count++进行循环,最后得到的count就是数组的元素个数。