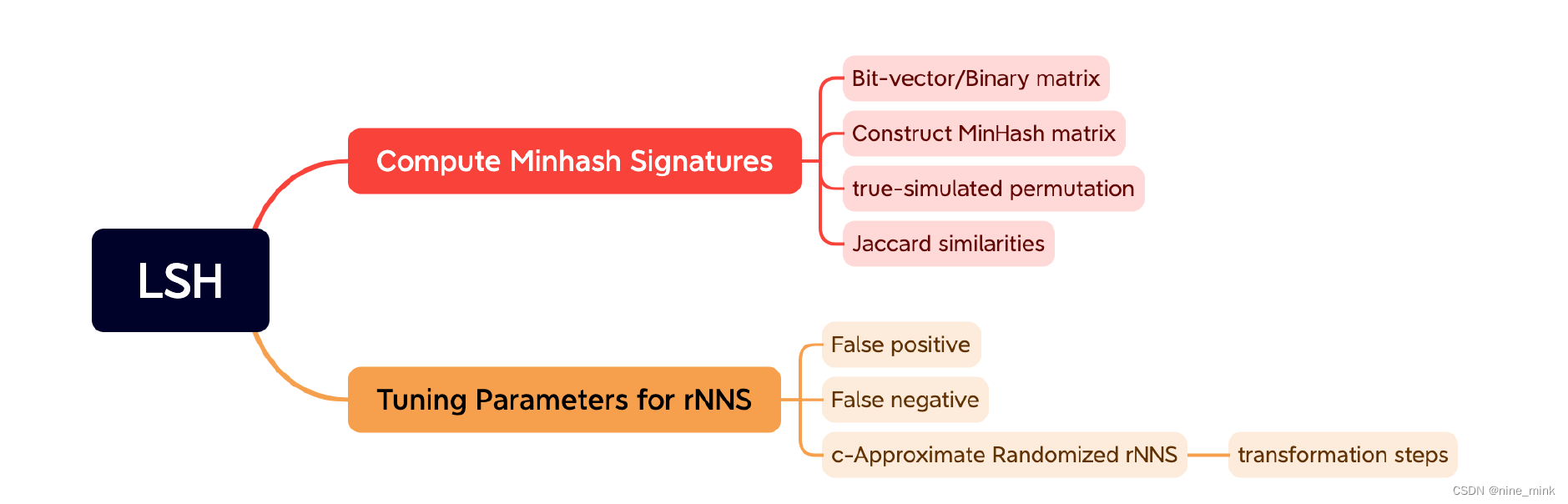
LSH Review
- Overall
- Minhash Signatures
- Binary Matrix（bit-vector）
- Construct MinHash matrix
- Generate simulated permutations
- Jaccard similarities
- Tuning Parameters for rNNS
Overall
hash就是将不同长度规则的文本转化成相同长度的字符串，用这些相同长度的字符串来表示原文本。但是传统 hash存在一个问题是，相同内容的文本会生成相同的 hash，但是相似的文本（可能就是一个字的差别）生成的 hash会有很大的不同。但是我们在做文本相似度时，希望对相似的文本生成相似的 hash，这样我们只需要计算一个个特定长度的 hash值之间相似度，就可以近似得到原文本之间的相似度了，显然传统的 hash算法是做不到这一点的 。
针对这个问题我们就要设计一种hash算法，让相似的文本生成相似的 hash值。
MinHash each set/document into a hash table Only compute Jaccard similarity of any pair of sets in the same bucket
Minhash Signatures
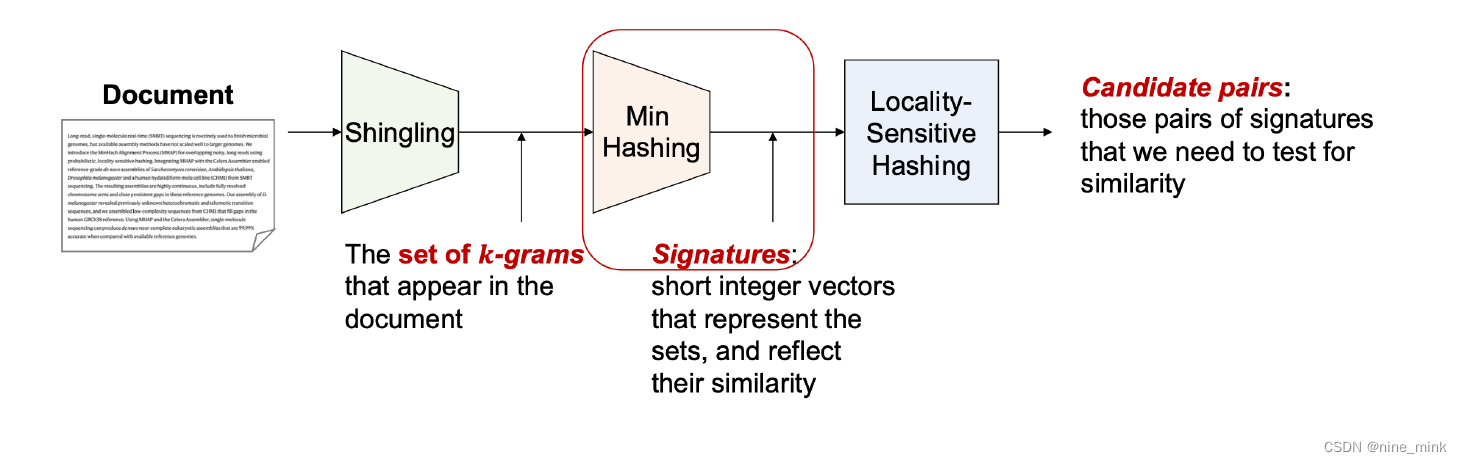Question
Binary Matrix（bit-vector）
Universe = {1，2，3，4，5，6，7}
D1 has {1，2，5，6，7}
Hence, D1[1] = D1[2] = D1[5] = D1[6] = D1[7] =1, while D1[3] = D1[4] = 0, so on and so forth.
（A）Answer
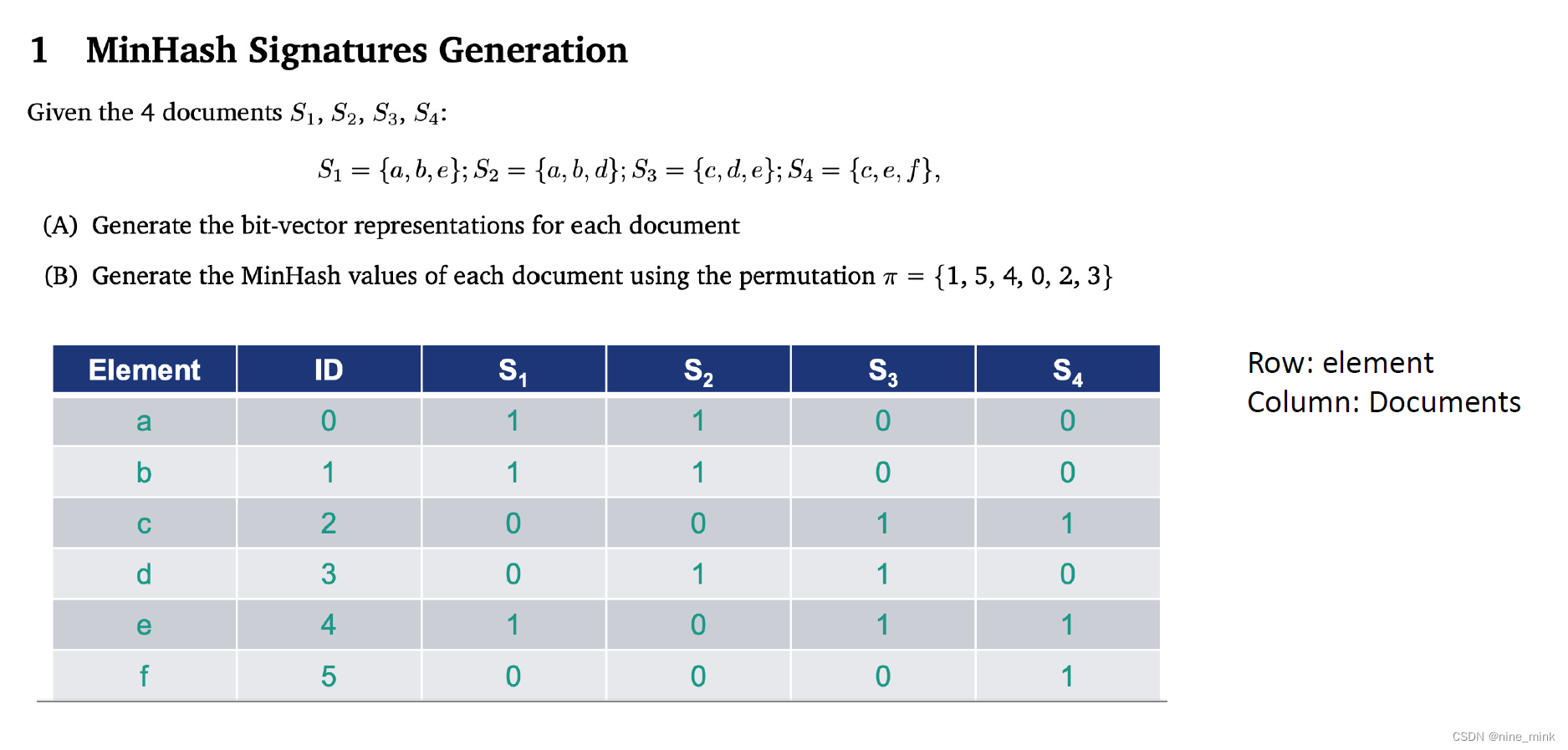
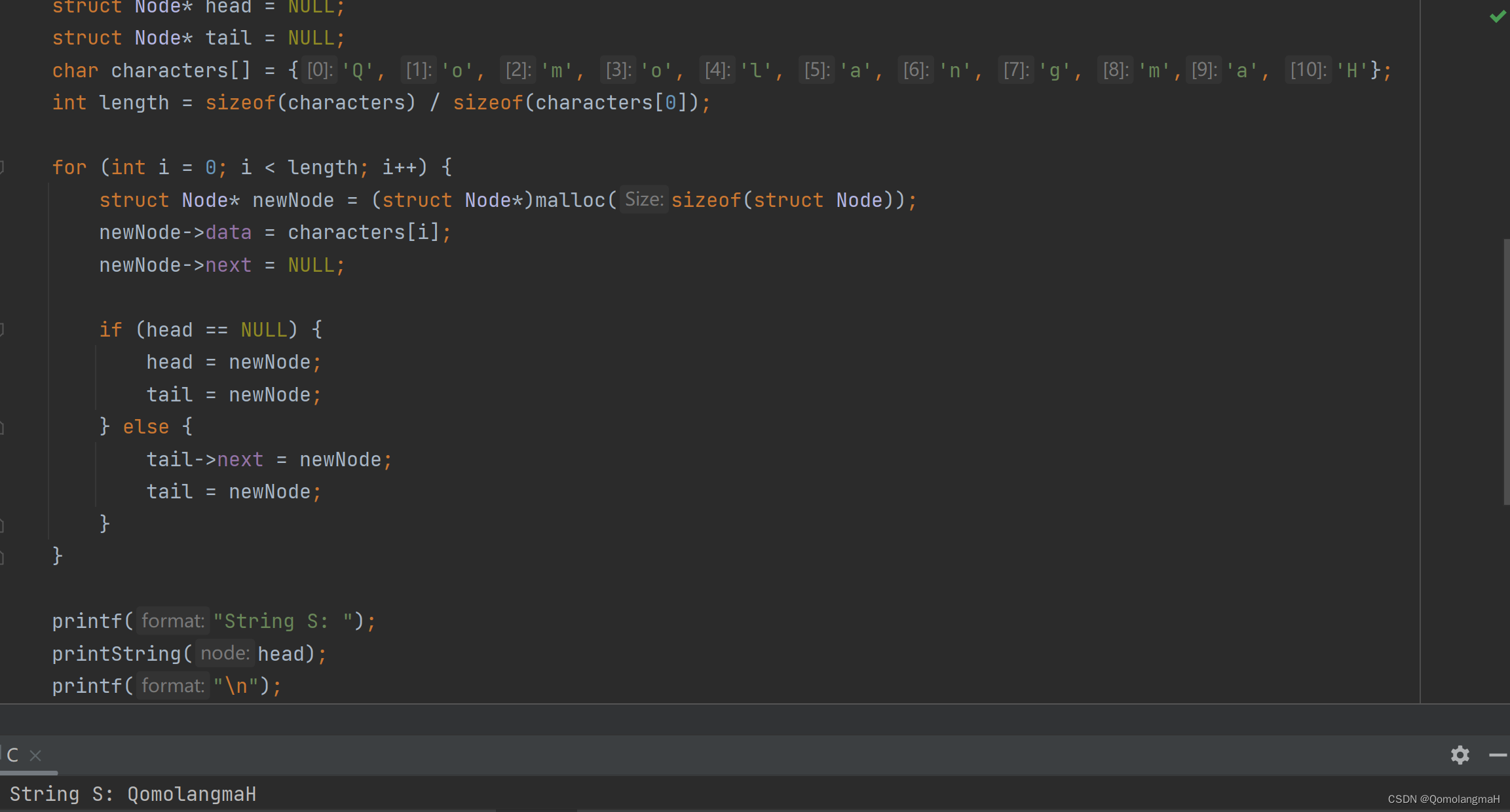
Construct MinHash matrix
在minhash算法中是怎么生成 hash的呢 可以用如下 3步来简单理解如何生成 hash
-
将行随机打乱。
-
行打乱后，针对每个 S1、 S2、 S3看第一个 1所在的行号，这个行号就是这个集合的最小值就是 MinHash Value。
-
设定 hash的大小，如果是 N，则重复上述步骤，随机进行 N次行打乱， 得到 N个最小哈希值，那么这 N个 MinHash Value组成的集合就是 S1、 S2、 S3 MinHash Signature
所以，MinHash Signature 是 N个 MinHash Value组成的集合
比如，对于红色的第一列随机行号S1来说，D1的一列中D1[n] == 1所对应的行号的集合为{4，2，6，3，5}，其中最小的是2，所以D1在S1上的MinHash Value是2，以此类推。
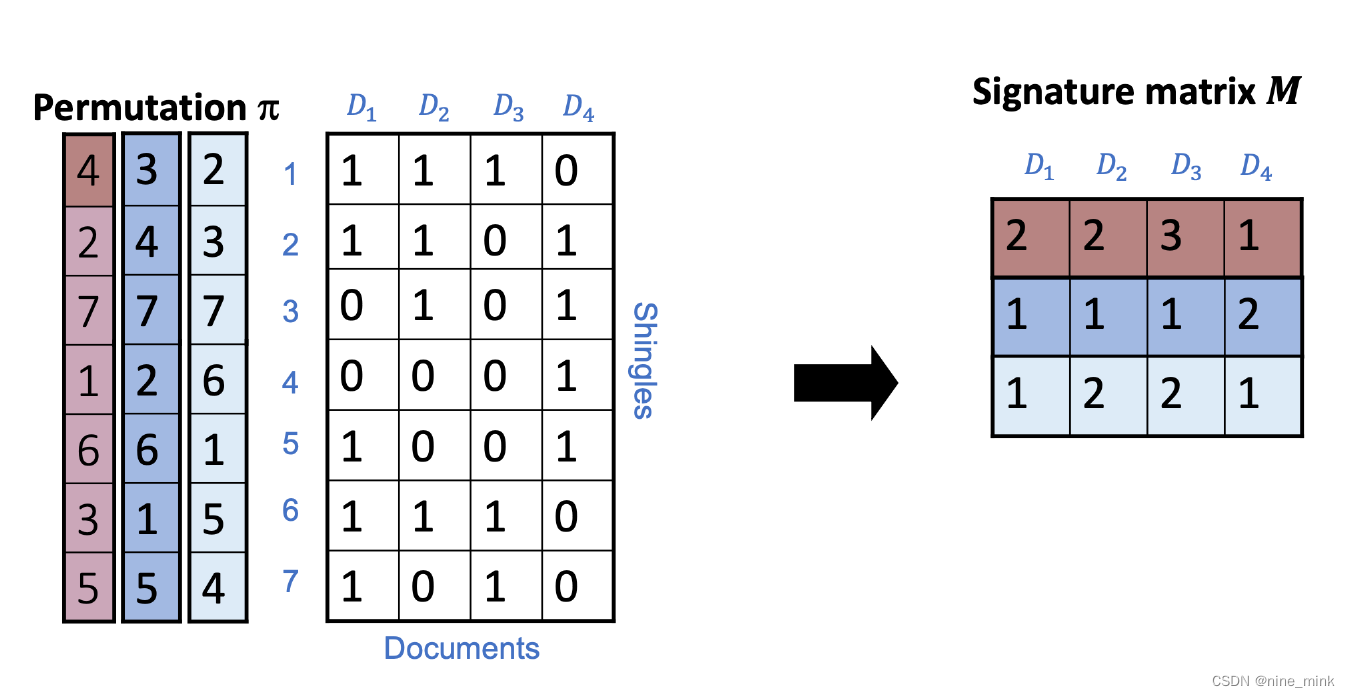
（B）Answer
Generate simulated permutations
Question
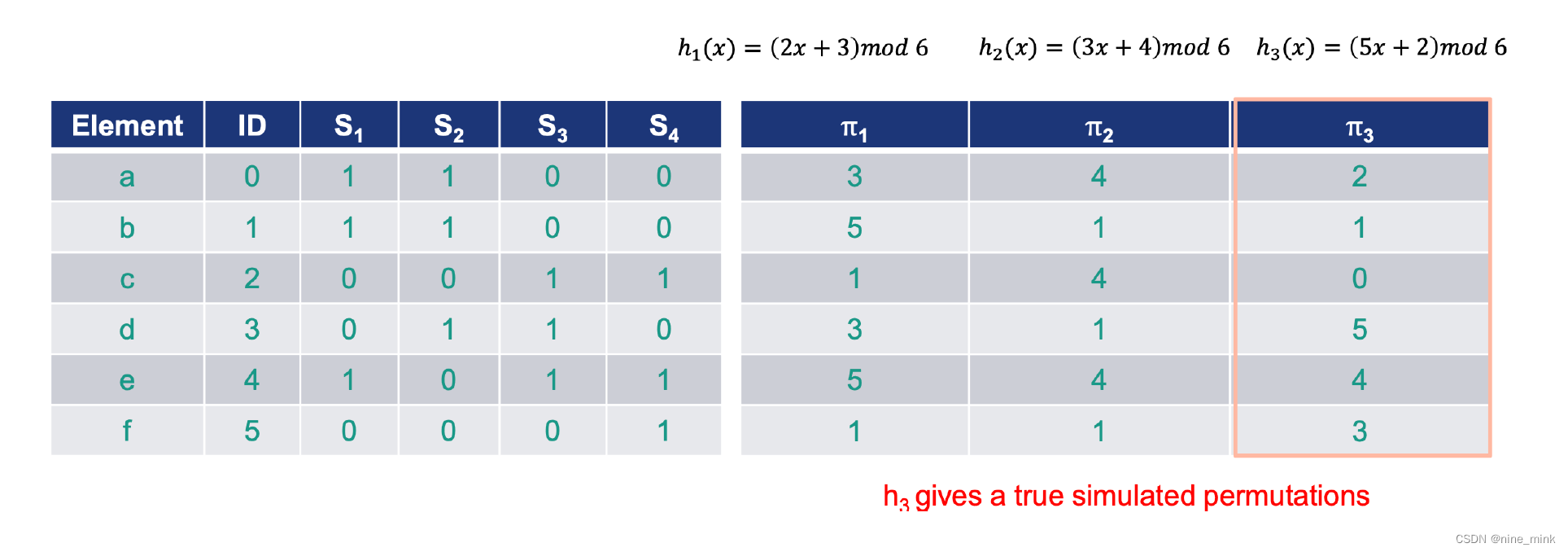
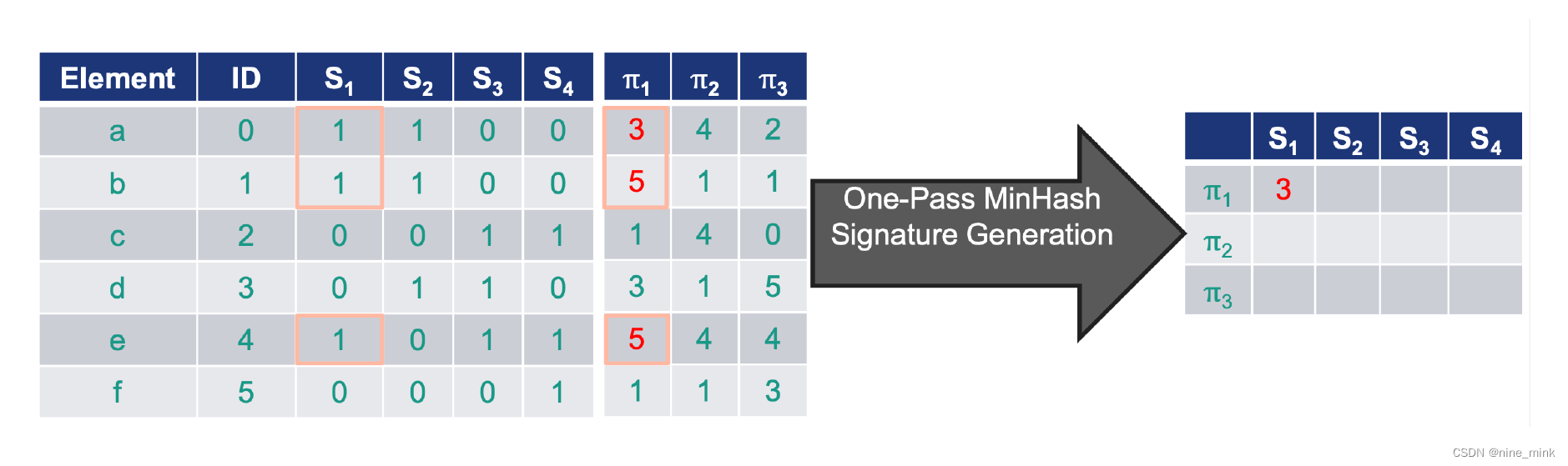
Jaccard similarities
Example
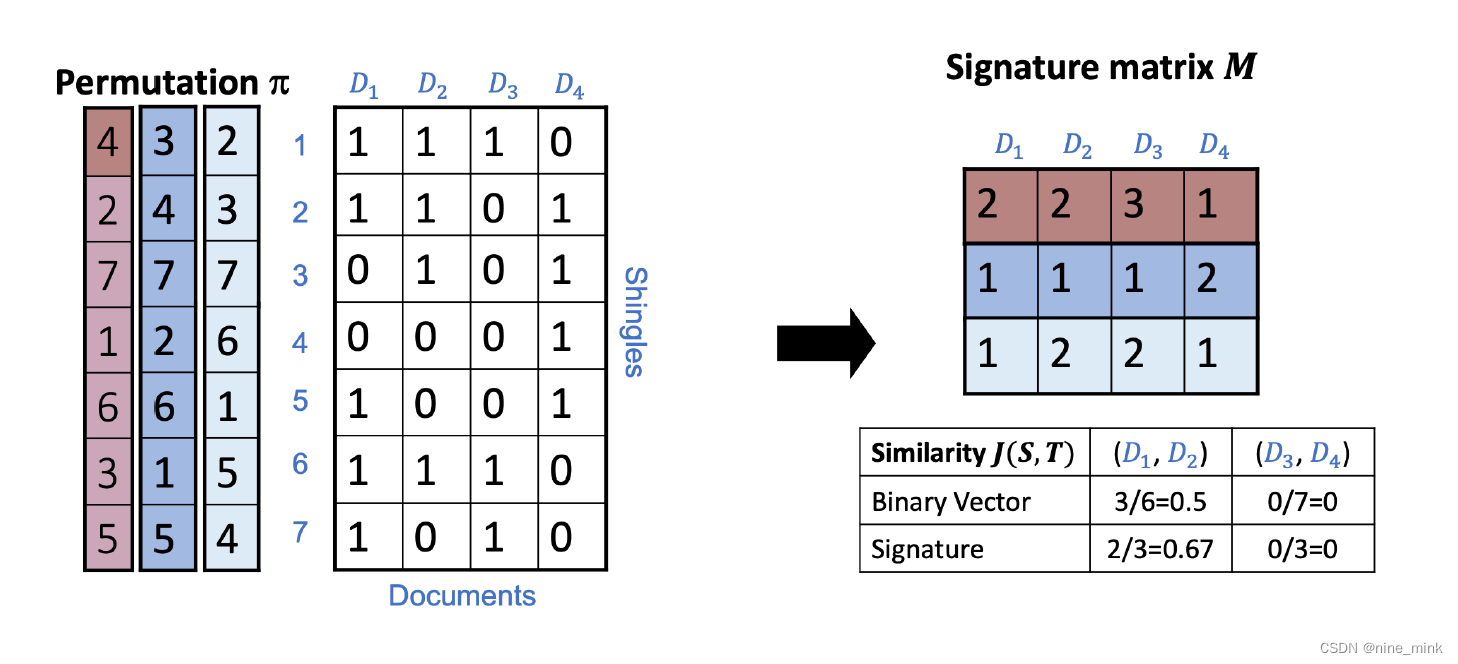
Answer
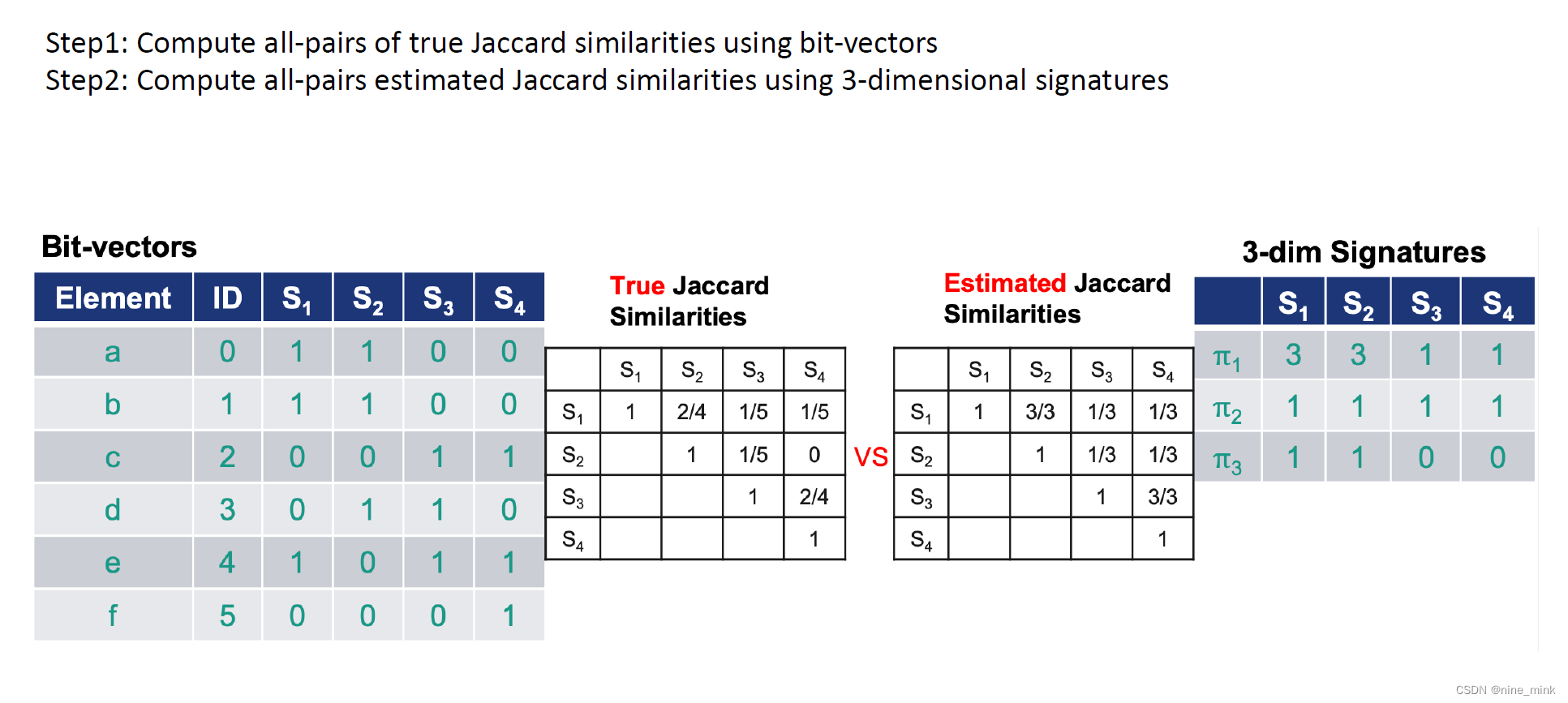
Tuning Parameters for rNNS
LSH (Locality Sensitivity Hashing, 局部敏感哈希)算法通过上面的Min Hashing可以将一个大矩阵通过哈希映射压缩成一个小矩阵，同时保持各列之间的相似性，从而降低了复杂度。但是，虽然我们降低了特征复杂度，如果用户非常多的话，我们的计算量依然是非常大的（O(n**2)），如果我们能先粗略地将用户分桶，将可能相似的用户以较大概率分到同一个桶内，这样每一个用户的“备选相似用户集”就会相对较小，降低寻找其相似用户的计算复杂度，LSH就是这样一个近似算法。
LSH的具体做法是在Min Hashing所得的signature向量的基础上，将每一个向量分为几段，称之为band（即每个band包含多行），如下图所示
每个signature向量被分成了4段，图上仅展示了各向量第一段的数值。其基本想法是：如果两个向量的其中一个或多个band相同，那么这两个向量就可能相似度较高；相同的band数越多，其相似度高的可能性越大。所以LSH的做法就是对各个用户的signature向量在每一个band上分别进行哈希分桶来计算相似度，在任意一个band上被分到同一个桶内的用户就互为candidate相似用户，这样只需要计算所有candidate用户的相似度就可以找到每个用户的相似用户群了。
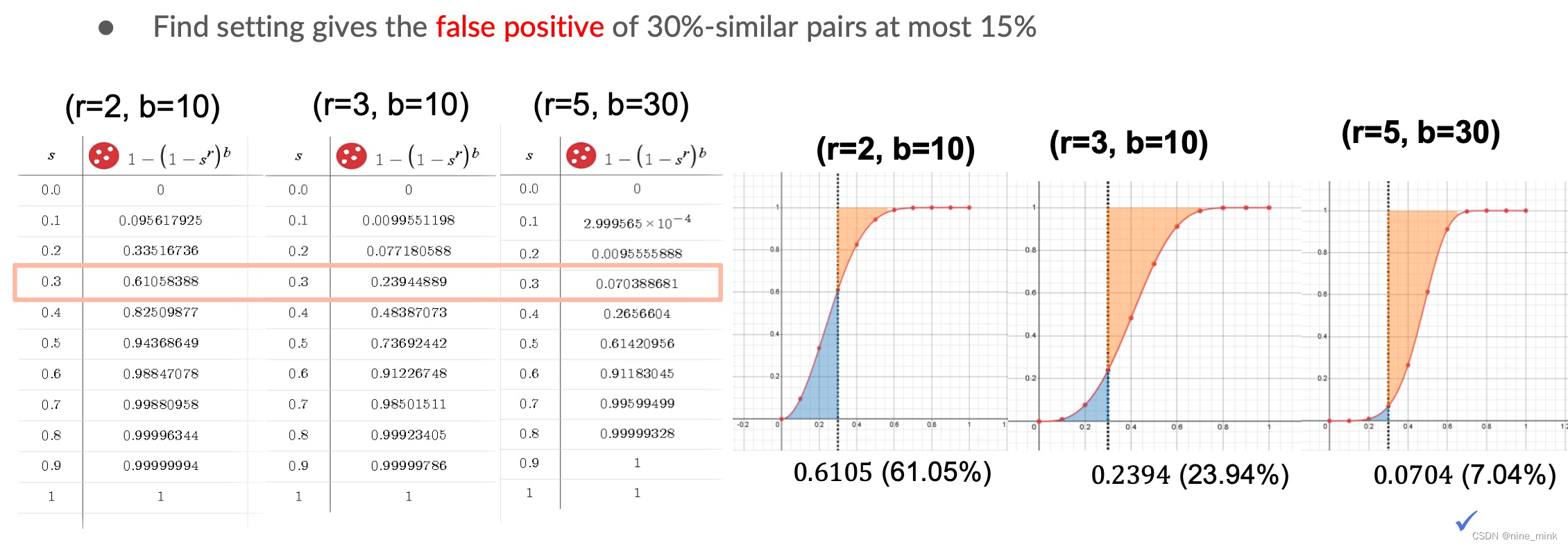
下面我们对signature向量的分桶概率作一些数值上的分析，以便针对具体应用确定相应的向量分段参数。假设我们将signature向量分为b个band，每个band的大小（也就是band内包含的行数）为r。假设两个用户向量之间的Jaccard相似度为s，前面我们知道signature向量的任意一行相同的概率等于Jaccard相似度s，我们可以按照以下步骤计算两个用户成为candidate用户的概率：
- 两个signature向量的任意一个band内所有行的值都相同的概率为sr;
- 两个signature向量的任意一个band内至少有一行值不同的概率为1-sr;
- 两个signature向量的所有band都不同的概率为(1-sr)b;
- 两个signature向量至少有一个band相同的概率为1-(1-sr)b，即为两个用户成为candidate相似用户的概率；
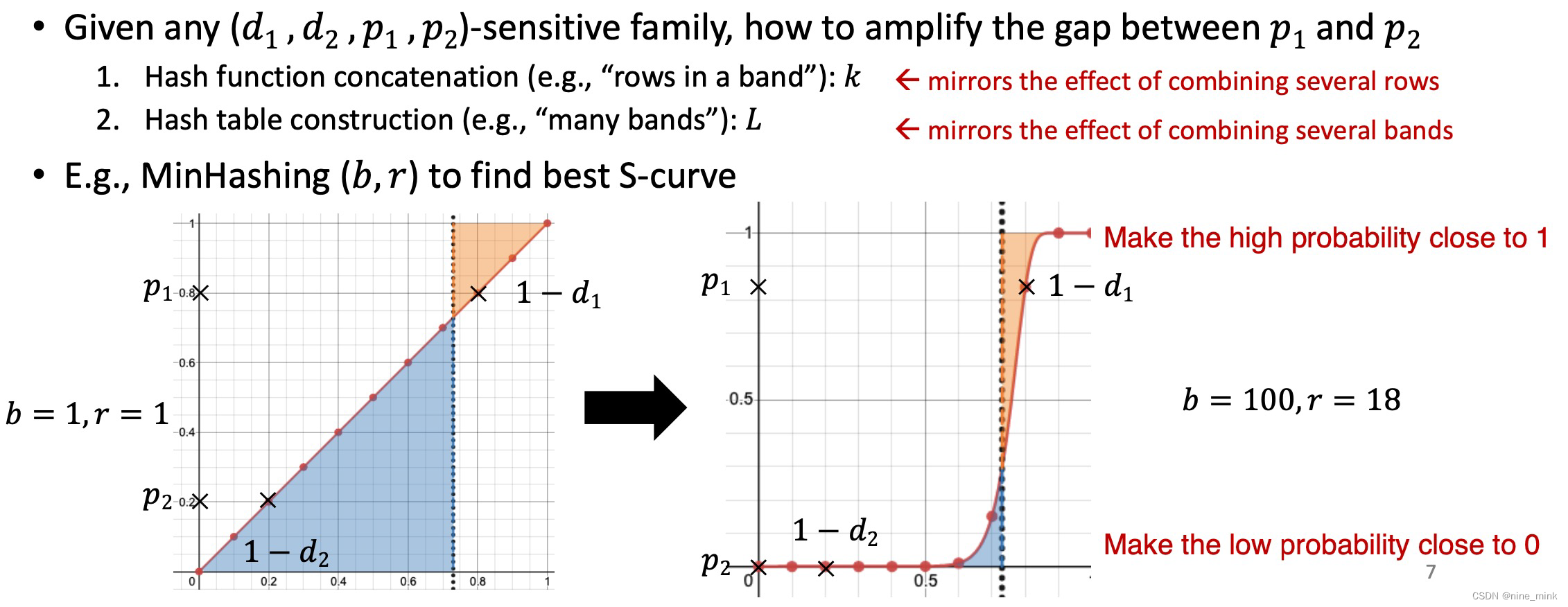
（A）Answer
Y – axis: Probability of being a candidate
False Positives: 相似度很低的两个用户被哈希到同一个桶内
False Negatives: 真正相似的用户在每一个band上都没有被哈希到同一个桶内
（B）Answer
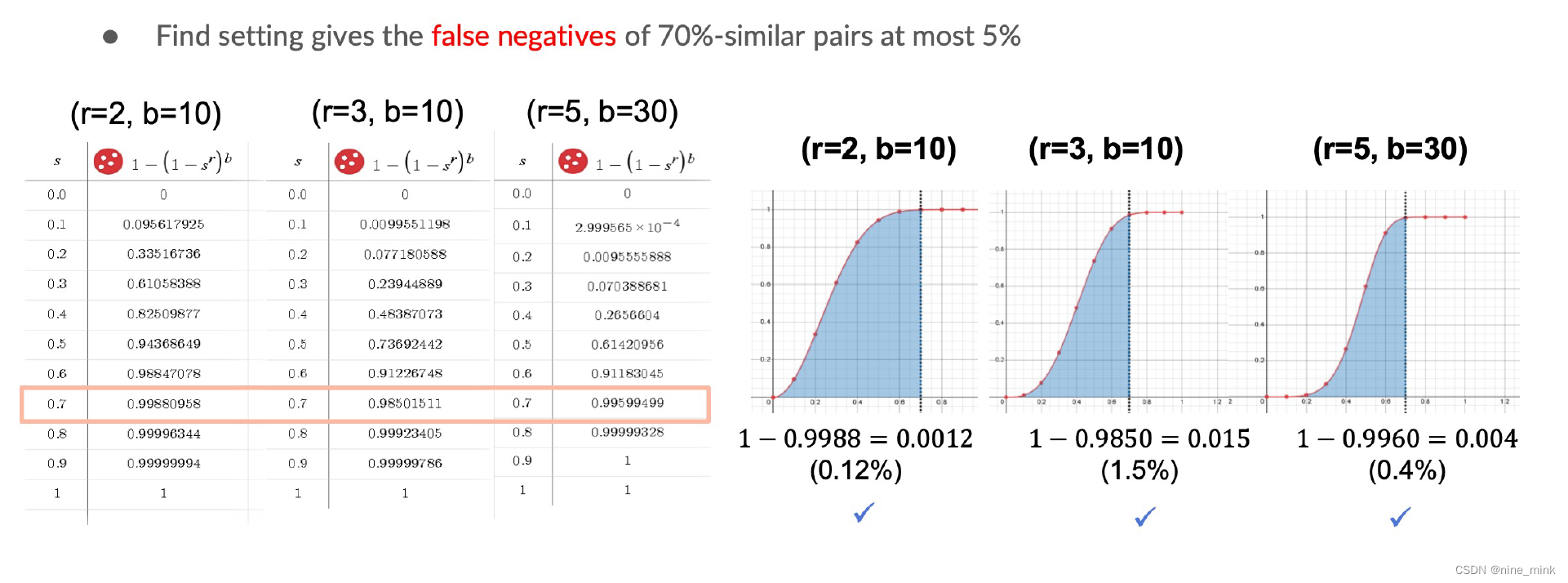
（C）Answer
