《TiNeuVox:Fast Dynamic Radiance Fields with Time-Aware Neural Voxel》
链接:https://jaminfong.cn/tineuvox/
摘要
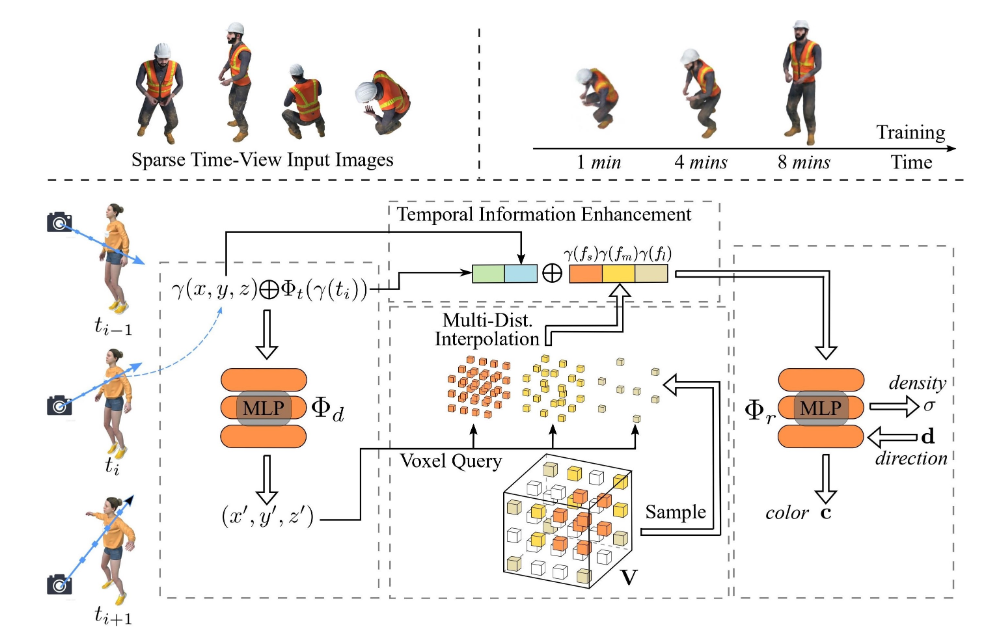
作者通过表示具有时间感知体素特征的场景提出了一个辐射场框架,并将其命名为 TiNeuVox。作者引入了一个微小的坐标变形网络来模拟粗略的运动轨迹,并且在辐射网络中进一步增强了时间信息。提出了一种多距离插值方法,并将其应用于体素特征,以对小运动和大运动进行建模。作者所提出的框架明显加速了动态辐射场的优化,同时保持了高渲染质量。对合成场景和真实场景都进行了实证评估。作者所提出的 TiNeuVox 仅用 8 分钟和 8 MB 的存储成本就完成了训练,同时显示出与以前的动态 NeRF 方法相似甚至更好的渲染性能。
《SelfNeRF: Fast Training NeRF for Human from Monocular Self-rotating Video》
链接:https://arxiv.org/pdf/2210.01651.pdf
摘要
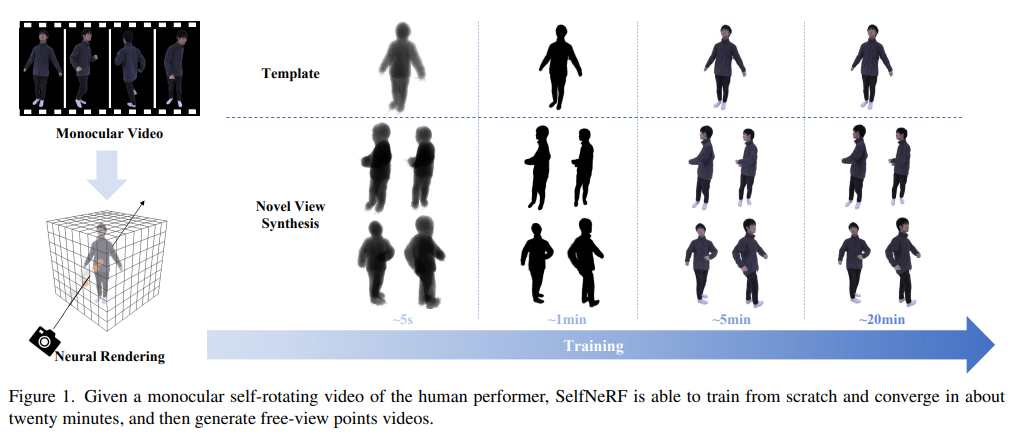
在本文中,作者提出了 SelfNeRF,这是一种基于神经辐射场的高效人体表征的新型视图合成方法。给定表演者的单目自旋转视频,SelfNeRF 可以从头开始训练并在大约二十分钟内获得高保真结果。最近的一些成果利用神经辐射场进行动态人体重建。然而,这些方法中的大多数都需要多视图输入并且需要数小时的训练,因此仍然难以实际使用。为了解决这个具有挑战性的问题,我们引入了一种基于多分辨率哈希编码的表面相对表示,可以大大提高训练速度并聚合帧间信息。在几个不同数据集上的广泛实验结果证明了 SelfNeRF 对具有挑战性的单目视频的有效性和效率。
实验效果
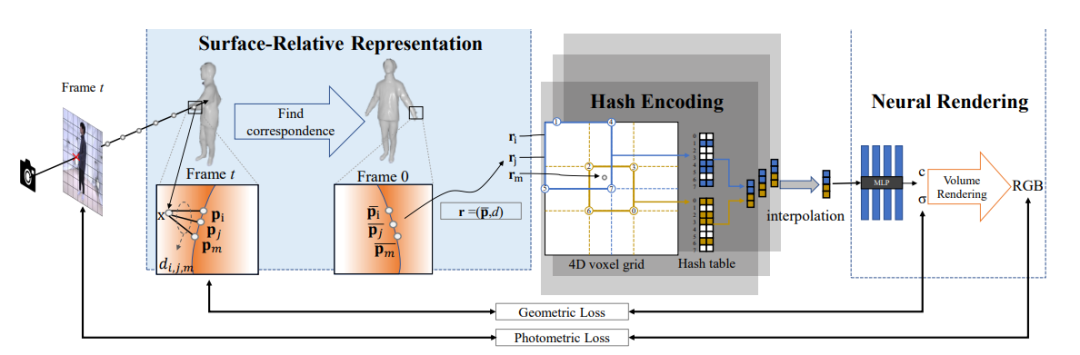
系统架构
创新点
1)SelfNeRF 是第一个将哈希编码应用于动态人体的论文,它可以在几十分钟内重建一个人的动态神经辐射场。
2)提出了一种表面相关的哈希编码来聚合帧间信息,并显着加快人体神经辐射场的训练。
3)借助最先进的人体重建方法,作者可以用单目相机重建人体表现的高保真新视图合成。