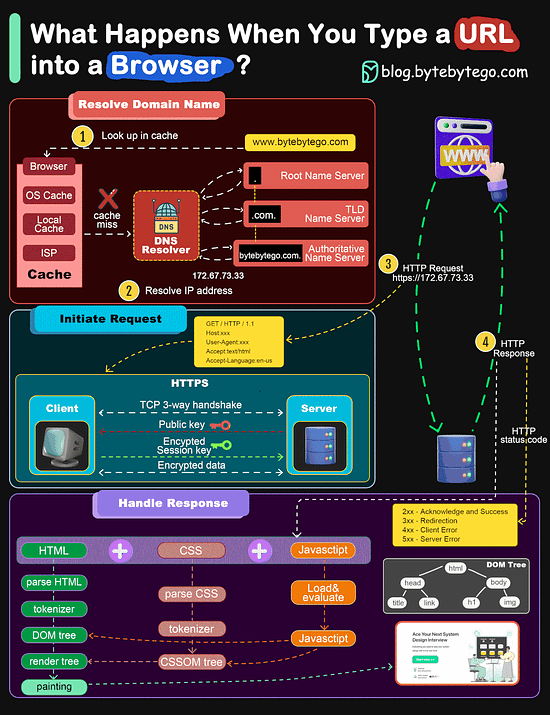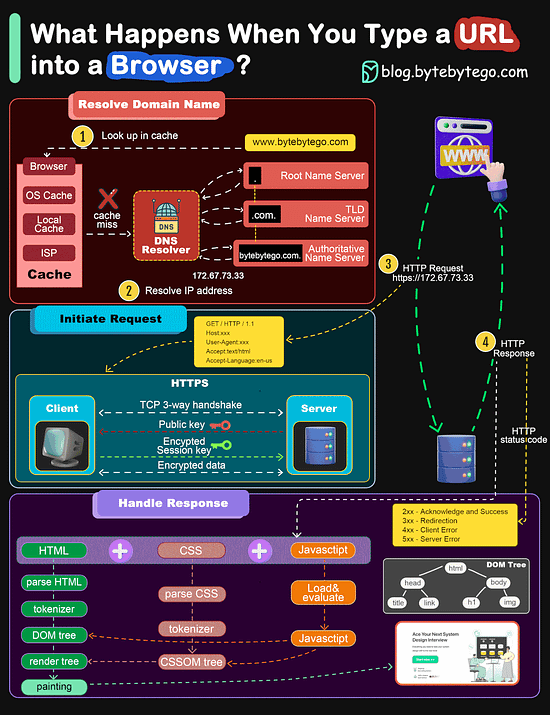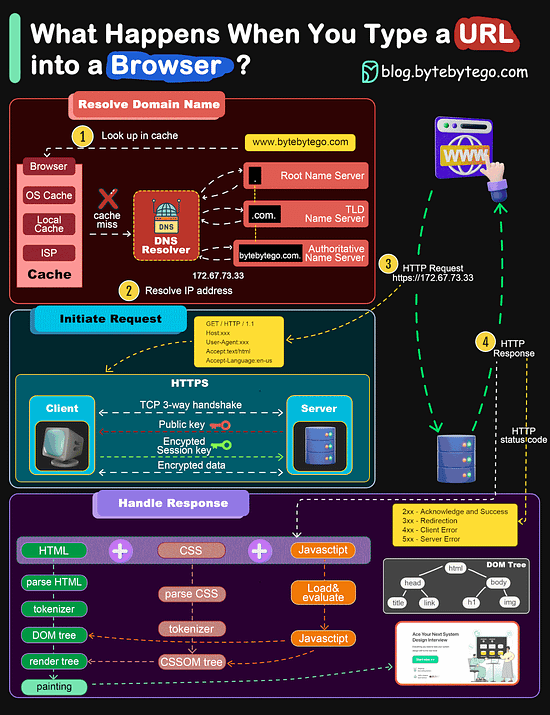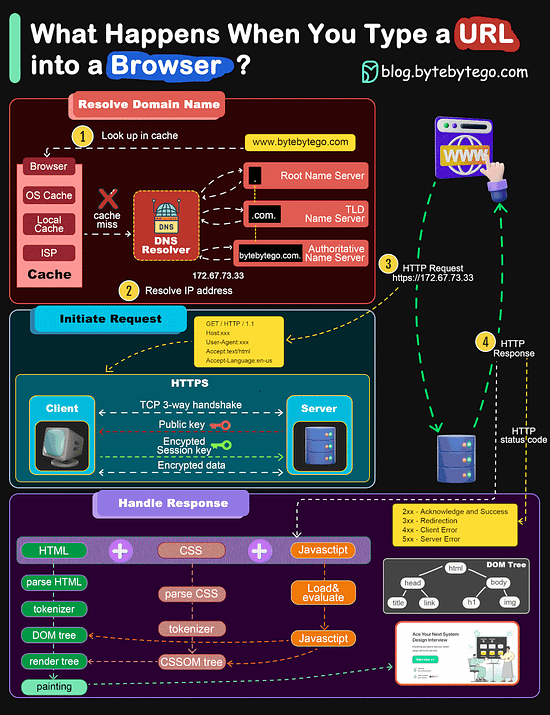
从感知机到神经网络

在感知机中，参数的值需要我们人工去设置，神经网络的出现就是解决这一问题，具体的讲，神经网络的一个重要性质就是它可以自动地从数据中学习到合适的权重参数

神经网络的例子

最左边称为输入层，最右边为输出层，中间称为中间层或者隐藏层。隐藏层的神经元肉眼看不到。

从输入层到输出层以此称为第0层，第1层……

图中由3层神经元组成，但是实际上只有两层神经元有权重，因此称为2层网络，神经网络的形状类似与感知机。

复习感知机

感知机接收x1和x2两个输入信号，输出y。

$$y=\{\begin{array}{l}0，(b+w1x1+w2x2)\le 0\\ 1，(b+w1x1+w2x2)>0\end{array}$$
b称为偏置，用于控制神经元被激活的容易程度。

wi表示每个信号的权重的参数，用于控制各个信号的重要性。

将上面公式改写为更加简洁的形式。用一个新的函数来表示这种分情况的动作，引入h(x)
$$y=h(b+w1x1+w2x2)$$

$$h(x)=\{\begin{array}{l}0，x\le 0\\ 1，x>0\end{array}$$
输入信号的综合会被函数h(x)转换，转化后的值就是y，其实改写之后的函数和之前的函数做的是相同的事情。

激活函数

h(x)函数会将输入信号的总和转化为输出信号，这种函数一般称为激活函数，**激活函数的作用在于如何激活输入信号的总和。**进一步改写公式
$$a=b+w1x1+w2x2$$

$$y=h(a)$$

分两个阶段处理，先计算输入信号的加权总和，然后用激活函数转化这一总和输出y。

• a表示输入信号的总和
• h()表示激活函数
• y表示输出

激活函数就是连接感知机和神经网络的桥梁！！！

激活函数

$$h(x)=\{\begin{array}{l}0，x\le 0\\ 1，x>0\end{array}$$

上式表示的激活函数以阈值为界，一旦输入超越阈值，就会切换输出，也可以叫做阶跃函数。因此感知机中使用了阶跃函数作为激活函数。在激活函数的众多候选函数中，感知机使用了阶跃函数。那么感知机使用其他函数作为激活函数的话，就可以进入神经网络的世界了。

sigmoid函数

$$h(x)=\frac{1}{1+exp(-x)}$$

exp(-x)表示e^-x的意思，神经网络中用sigmoid函数作为激活函数，进行信号的转化，转化后的信号被传送给下一个神经元，感知机和神经网络的主要区别就是在于这个激活函数。

阶跃函数的实现

当输入超过0时，输出1，否则小于1

import numpy as np
def step_function1(x):
    if x>0:
        return 1
    else:
        return 0

但是这种写法x只能接收实数，不支持numpy数组，修改为支持numpy的格式

import numpy as np
def step_function(x):
    y = x>0
    return y.astype(np.int64) # 将布尔类型转化为int型
x=np.array([-1.0,2.0,1.0])
print(step_function(x))

上述代码对numpy数组使用了不等号运算

阶跃函数的图形

import numpy as np
import matplotlib.pylab as plb
def step_function(x):
    return np.array(x>0,dtype=np.int64)
x=np.arange(-5.0,5.0,0.1)
y=step_function(x)
plb.plot(x,y)
plb.ylim(-0.1,1.1) # 指定y轴的范围
plb.show()

**x=np.arange(-5.0,5.0,0.1)**表示在-5.0到5.0的范围内，以0.1为单位，生成numpy数组[-0.5,-4.9,……,4.9]。

sigmoid函数的图形

import numpy as np
import matplotlib.pylab as plb
def step_function(x):
    return 1/(1+np.exp(-x))
x=np.arange(-5.0,5.0,0.1)
y=step_function(x)
plb.plot(x,y)
plb.ylim(-0.1,1.1)
plb.show()

在sigmoid函数中之所以支持numpy函数，是因为numpy数组具有广播功能，标量和numpy数组进行运算时，标量会和numpy数组中的各个元素进行运算

sigmoid函数与阶跃函数比较

不同：

• 二者图形的平滑性不同，sigmoid函数是一条平滑的曲线，输出随着输入发生连续性的变化。而阶跃函数以0为界，输出发生急剧性的变化。sigmoid函数的平滑性对神经网络的学习具有重要意义。

• 阶跃函数只能返回0或1，sigmoid函数可以返回0.731……，0.880……等实数。也即是感知机中神经元之间流动的是0或者1，而神经网络中流动的是连续的实数值。

共同：

• 虽然在平滑性上有差异，但是从宏观角度来说二者具有相似的形状，输入信号重要时，输出值较大，否则输出就越小
• 二者都为非线性函数

非线性函数

神经网络的激活函数必须使用非线性函数

线性函数的问题在于不管加深层数，总是存在与之等效的“无隐藏层的神经网络”

比如线性函数h(x)=cx作为激活函数，y=h(h(h(x)))的运算对应三层神经网络，这个运算就等于c * c * c * x的乘法运算，再次化简为a* x ，表示为没有隐藏层的神经网络。

ReLU函数

sigmoid函数在很早就开始使用了，而最近主要使用ReLU函数
$$h(x)=\{\begin{array}{l}0，x\le 0\\ x，x>0\end{array}$$
在输入>0时，直接输出该值，在输入<=0时，输出0

import numpy as np
import matplotlib.pylab as  plb
def ReLU_function(x):
    return np.maximum(x,0)
x=np.arange(-5.0,5.0,0.1)
y=ReLU_function(x)
plb.plot(x,y)
plb.ylim(-0.1,5.0)
plb.show()

这里使用了numpy的maximum函数，maximum函数会从输入的数值中选择较大的值输出

多维数组的运算

多维数组

多维类似与线性代数里的矩阵，使用numpy数组生成多维数组。

import numpy as np
a = np.array([1,2,3,4])
b = np.array([[1,2],[3,4],[5,6]])
print("a的维度=",a.ndim)  # 维度
print("a的形状",a.shape) # 形状
print("b的维度=",b.ndim)  # 维度
print("b的形状",b.shape) # 形状

a的维度= 1
a的形状 (4,)
b的维度= 2
b的形状 (3, 2)

数组的维数可以通过np.dim()函数获得。

数组的形状可以通过np.shape()函数获得。

在上面代码中，a是一维数组，由4个元素组成,a.shape的结果是个元组，这是因为一维数组的情况也要返回与多维数组一致的结果。

b数组为3 x 2的矩阵，表示第一维度有3个元素，第二维度有2个元素

二维数组也成为矩阵

矩阵乘法

import numpy as np
A = np.array([[1,2],[3,4],[5,6]])
"""
[[1 2]
 [3 4]
 [5 6]]
 
"""
B = np.array([1,1])
"""[1 1]"""
print(np.dot(A,B))
"""[ 3  7 11]"""

这里数组B可以转化为1 x 2或者2 x 1的形式，为了计算的适应。

import numpy as np
A = np.array([[1,2],[3,4],[5,6]])
print(A)
B = np.array([[1,1],[2,3],[1,2]])
print(B)
print(np.dot(A,B))

Traceback (most recent call last):
  File "D:\pythonProject\pythonStudy\多维数组的运算\矩阵的乘法.py", line 6, in <module>
    print(np.dot(A,B))
ValueError: shapes (3,2) and (3,2) not aligned: 2 (dim 1) != 3 (dim 0)

对应维度不一致报错

神经网络的内积

在下图中是一个除去激活函数和偏置参数的神经网络

$$\begin{gathered} 输出求和公式y=x1\ast w1+x2\ast w2和矩阵内积类似， \\ 将这种简单化为矩阵相乘的方式 \end{gathered}$$
X W = y

(x1,x2)
(x1 * 1 + x22,x1 * 3 + x24,x1 * 5 + x2*6)

import numpy as np
X = np.array([4,5])
W = np.array([[1,3,5],[2,4,6]])
print(np.dot(X,W))

三层神经网络的实现

三层神经网络：输入层有两个神经元，第1个隐藏层有3个神经元，第2个隐藏层有2个神经元，输出层有两个神经元

符号确认

图中突出显示了从输入层神经元X2到第一隐藏层a1的权重。

权重和隐藏层的神经元右上角有一个（1），表示第一层的权重和第一层神经元。此外右下角有两个数字，是后一层的神经元和前一层的神经元的索引号

各层间信号传递的实现

使用矩阵的运算，改写为另一种形式。

import numpy as np
X=np.array([0.12,0.24])
W1=np.array([
    [1,2,3],
    [2,3,4]
])
B1=np.array([0.1,0.2,0.3])
A1=np.dot(X,W1)+B1
Z1=sigmoid(A1)
print(Z1) #[0.66818777 0.76133271 0.83479513]

隐藏层的加权和用a来表示，被激活函数sigmoid函数转换后的信号用z来表示。

上图为输入层到第1层的信号传递，接下来实现第1层到第2层

B2=np.array([0.1,0.2,0.3])
W2=np.array([
    [1,2],
    [2,3],
    [1,2]
])
A2=np.dot(Z1,W2)+B2
Z2 = sigmoid(A2)

最后是第2层到输出层的函数

B3=np.array([0.1,0.2])
W3 =  np.array([
    [1,2],
    [2,3],
])

A3=np.dot(Z2,W3)+B3
Y = identity_function(A3)

最后输出层使用了identity_function恒等函数，恒等函数会将输入按照原样输出

代码总结

import os, sys

sys.path.append(os.pardir)
import numpy as np
from common.functions import sigmoid, identity_function

# 权重和偏置的初始化
def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['B1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['B2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['B3'] = np.array([0.1, 0.2])
    return network

#从输入层到输出层信号的转化
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    B1, B2, B3 = network['B1'], network['B2'], network['B3']
    # 输入层到第一层
    A1 = np.dot(x, W1) + B1
    Z1 = sigmoid(A1)
    # 第一层到第二层
    A2 = np.dot(Z1, W2) + B2
    Z2 = sigmoid(A2)
    # 第二层到输出层
    A3 = np.dot(Z2, W3) + B3
    Y = identity_function(A3)
    return Y


network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)

输出层的设计

神经网络可以用在分类问题和回归问题上，需要根据实际情况改变输出层的函数，一般回归问题用恒等函数，分类问题使用softmax函数

机器学习的问题大致分为回归问题和分类问题

回归问题：比如根据一个人的图像能够预测这个人的体重的问题

分类问题：区分图像中的人是男性还是女性

恒等函数和softmax函数

恒等函数

会将输入按原样输出，对输入的信息不加任何改动直接输出

def identity_function(x):
    return x

softmax函数

计算第K个神经元的输出y_k ,分子是输入信号a_k的指数，分母是所有输入信号的指数和
$$y=\frac{e^{a_k}}{{\sum }_{i=1}^n{e}^{a_i}}$$

def softmax(x):
    exp_a = np.exp(x)
    exp_sum = np.sum(np.exp(x))
    y = exp_a / exp_sum
    return y

实现softmax函数注意事项

缺陷就是溢出问题，再函数中要进行指数运算，在超大值进行除法运算时会出现指数运算，结果会出现不确定情况

因为在计算机处理数时，数值必须在4字节或者8字节的有限数据宽度内，意味着存在有效位数，数值范围时有效的，因此会出现超大值无法表示的问题

softmax函数可以进行改进

这里的C^/一般会使用输入信号的最大值

def softmax(x):
    C=np.max(x)
    exp_a = np.exp(x-C)
    exp_sum = np.sum(np.exp(x-C))
    y = exp_a / exp_sum
    return y
x = np.array([0.3,2.9,4.0])
print(softmax(x)) #[0.01821127 0.24519181 0.73659691]

softmax函数特征

输出是0.0到1.0之间的实数，并且函数的输出值总和为1，因此把softmax函数的输出解释为概率。并且x的各元素大小关系和y的各元素大小关系并没有改变，比如x的最大值为第2个元素，y的最大值也为第2个元素。神经网络只把输出值最大的神经元所对应的类别作为识别结果，即便使用softmax函数，输出值最大的神经元位置也不会改变，在实际问题中，输出层的softmax函数一般会省略

输出层的神经元数量

输出神经元数量需要根据待解决问题来决定，比如某个输入图像，预测是图中数字0~9的哪一个问题，可以将神经元设定为10个